定義域がある指数関数と対数関数には最大値や最小値が存在する場合があります。
範囲によっては値が存在しないときもありますがそれも含めての解き方です。
関数なのでグラフを意識しながら解くのが手っ取り早いです。
もちろん、指数や対数の基本条件は満たしていなければなりません。
指数関数・対数関数の最大値、最小値を求めるときの基本
指数や対数の最大値、最小値問題でややこしく感じるのは、
定義域 \( x\) が \(\,a\,≦\,x\,≦\,b\,\) などとは与えられず、
\(\hspace{10pt} a\,≦\,m^x\,≦ \,b\)
のように直接は与えられていないことが多いからですが、
指数、対数の基本通り置換したあと、関数の最大最小を調べれば良いだけです。
(1)
\(x\) の取り得る範囲が \( 0 \,< \,3^x \,≦\,1\) であるとき、
関数 \(\displaystyle f(x) =3^{2x+1}-2\cdot 3^{x-1}-\frac{7}{3}\)
の最大値と最小値、およびそのときの \(x\) の値を求めよ。
(2)
関数 \(\displaystyle f(x) =(\log_{2}2x)^2-\log_{4}x^2 \)
の最小値とそのときの \( x\) の値を求めよ。
やっと指数「関数」という感じがしてきました。
指数・対数の基本法則を覚えた今、恐れるものは何もありません。
良いですか?
指数対数の難しい問題は数学Ⅲに回ります。笑
だから難しく考えず今までやってきたことを基本通りやって行けば大丈夫です。
「関数はグラフで考える!」 忘れないで下さい。
指数関数の最大値最小値を求める方法
(1)
「 \( x\) の取り得る範囲」は定義域のことです。
\(\hspace{10pt} 0\,< \,3^x\, ≦ \,1 \hspace{5pt} \Leftrightarrow \hspace{5pt} x\,≦ \,0\)
これはグラフからもすぐに分かるでしょう。
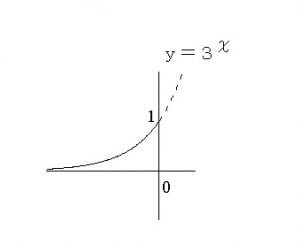
左(下限)はどこまで行っても正です。
\( y=3^x\) が負になることはありません。
この問題では関係ありませんが、一応確認しておきました。
では、関数 \( f(x)\) を考えましょう。
\(\hspace{10pt}\displaystyle f(x) = 3^{2x+1}-2\cdot 3^{x-1}-\frac{7}{3}\\ \\
\displaystyle =3\cdot 3^{2x}-2\cdot 3^{-1}\cdot 3^{x}-\frac{7}{3}\\ \\
\displaystyle =3\cdot 3^{2x}-2\cdot \frac{1}{3}\cdot 3^{x}-\frac{7}{3}\\ \\
\displaystyle =3\cdot 3^{2x}-\frac{2}{3}\cdot 3^{x}-\frac{7}{3}\)
と指数法則を利用し変形すると、\(3^x=t\) とおきたくなりませんか?なりますよね。
\(\,3^x\,=\,t\,\)とおくと問題の条件
\(\hspace{10pt} 0\,<3^x\,≦\,1\) から \( 0\,<\,t\,≦\,1\)
このとき
\(\hspace{10pt} f(x)=3\cdot 3^{2x}-\displaystyle \frac{2}{3}\cdot 3^{x}-\displaystyle \frac{7}{3}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} f(t)=3t^2-\displaystyle \frac{2}{3}t-\displaystyle \frac{7}{3}\)
と \(t\) の2次関数に変わりました。
この切り替えが重要です。
指数関数と2次関数の処理
置換したら指数関数だった問題が、2次関数の問題に置き換わったのです。
つまり、
「 \( 0 \,<\, t\, ≦ \,1\) における \( f(t)\) の最大・最小を求めよ。」
と同じです。
これ、どう見ても指数関数ではなく2次関数の基本問題ですよね。
では2次関数の最大・最小問題はどうするか?
『平方完成』 → 『グラフ』 です。
\(\hspace{10pt} f(t)=3t^2-\displaystyle \frac{2}{3}t-\displaystyle \frac{7}{3}\\ \\
=3\left(t^2-\displaystyle \frac{2}{9}t\right)-\displaystyle \frac{7}{3}\\ \\
=3\left(t^2-\displaystyle \frac{1}{9}\right)^2-3\cdot \displaystyle \frac{1}{81}-\displaystyle \frac{7}{3}\\ \\
=3\left(t^2-\displaystyle \frac{1}{9}\right)^2- \displaystyle \frac{1}{27}-\displaystyle \frac{63}{27}\\ \\
=3\left(t^2-\displaystyle \frac{1}{9}\right)^2- \displaystyle \frac{64}{27}\)
(平方完成は自分でやってみてください!)
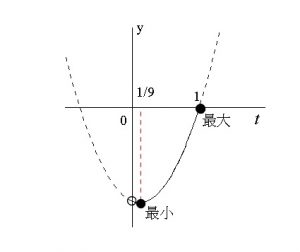
頂点が定義域内にあるので、最小値は頂点の \(y\) 座標です。
軸から遠い方が最大値になるので、
定義域の内で一番端になる \( t=1\) のときが最大になります。
グラフで確認しながら進めて下さい。
最大値・最小値を求めます。
\(\hspace{10pt} t=3^x=1\)
つまり \( \underline{ x=0 }\) のとき最大値 \( \underline{ 0 }\)
\(\hspace{10pt} t=3^x=\displaystyle \frac{1}{9}=3^{-2}\)
つまり \( \underline{ x=-2 }\) のとき最小値 \(\displaystyle \underline{ -\frac{64}{27} }\)
最大・最小を答えるときはそのときの \( x\) の値も添えておきましょう。
置換して自分でおいた\(\,t\,\)ではなく問題にある\(\,x\,\)で答えます。
対数関数の最大値最小値の求め方
(2)は対数関数ですが同じです。
底をそろえて、定義域を見て、なじみの関数に置きかえます。
\(\hspace{10pt} f(x) =(\log_{2}2x)^2-\log_{4}x^2 \)
真数条件は \( x>0\) ですが、底がそろっていません。
底をそろえるときはできるだけ素数にすると後が楽になることが多いです。
これはわかりやすいですね。
対数の法則と底の変換公式を使って底を2でそろえます。
\(\hspace{10pt}f(x) = (\log_{2}2x)^2-\log_{4}x^2 \\ \\
\displaystyle =(\log_{2}2 +\log_{2}x)^2-\frac{\log_{2}x^2}{\log_{2}{4}}\\ \\
\displaystyle = (1 + \log_{2}x)^2-\frac{2\log_{2}x}{\log_{2}{2^2}}\\ \\
\displaystyle = (1 + \log_{2}x)^2-\frac{2\log_{2}x}{2}\\ \\
=(1 + \log_{2}x)^2-\log_{2}x\)
展開処理する前に置換してしまいしょう。
\(\log_{2}x=t\) とおくと \( \color{red}{t}\) は実数全体です。
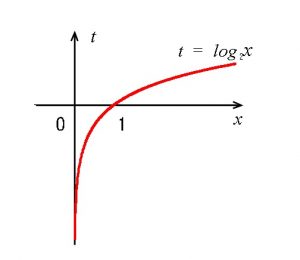
\(\hspace{10pt} f(x) = (1 + \log_{2}x)^2-\log_{2}x \\ \\
\Leftrightarrow \\ \\
\hspace{10pt}f(t) = (1 + t)^2-t \\ \\
=t^2+2t+1-t\\ \\
=t^2+t+1\\ \\
\displaystyle =\left( t+\frac{1}{2} \right)^2-\frac{1}{4}+1\\ \\
\displaystyle =\left( t+\frac{1}{2} \right)^2+\frac{3}{4}\)
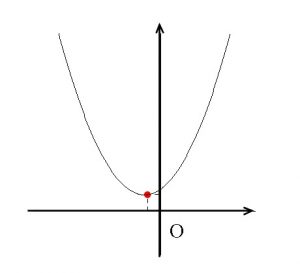
よって
\(\displaystyle t=-\frac{1}{2}\) つまり \(\displaystyle \log_{2}x=-\frac{1}{2}\)
のとき最小値をとります。
最大値はありません。
\(\hspace{10pt} \log_{2}x=-\displaystyle \frac{1}{2}\\ \\
\Leftrightarrow \hspace{5pt} x=2^{-\frac{1}{2}}=\displaystyle \frac{1}{2^\frac{1}{2}}=\displaystyle \frac{1}{\sqrt{2}} =\displaystyle \frac{\sqrt{2}}{2}\)
なので最小値は
\(\displaystyle x=\frac{\sqrt{2}}{2}\) のとき \(\displaystyle\underline{ \frac{3}{4} }\)
となります。
関数はグラフを利用すると見えてきます。
基本ですが大切なことですよ。
点数が取りにくい単元ではないので、共通テストで確実に得点源にしておきましょう。