微分係数と導関数の定義から微分の公式までの説明をしておきます。
微分では独特の表し方や記号があるので意味を確認しておきましょう。
本来なら連続性の確認からすべきなのですが、わかりづらくするので数学Ⅲに譲ります。
ここでは整関数が微分できるようになることを目的にします。3次関数までで大丈夫です。
微分係数の前に中学の復習をします。
直線の傾きを表す「平均変化率」からです。
平均変化率
関数 \(y=f(x)\) において
\( x\) が \( a\) から \( b\) まで変化するとき、
\( y\) の変化量は \( f(b)-f(a)\) となります。
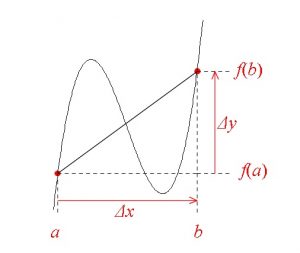
このときの変化の割合
\( \displaystyle \frac{f(b)-f(a)}{b-a}\)
を「平均変化率」といいます。
分母は \(x\) の増分
分子は \(y\) の増分
を表しています。
\(x\) の増分を \( \Delta x\), \(y\) の増分を \( \Delta y\)
とすると
\(\Delta x=b-a , \Delta y=f(b)-f(a)\)
のことですが、平均変化率は途中の増減は関係ありません。
図を見てもわかるとおり途中で増えても減っても、2点間の増減の平均としての2点の直線の傾きを表します。
この2点を限りなく小さな間隔にして表す平均変化率が微分係数です。
微分係数
平均変化率における分母は \( b-a\) ですが、
これは \(a\) からの増分を表しているので、
\( \color{red}{h}=b-a\)
とすればこの \( \color{red}{h}\) が \( x\) の増分とみることができます。
このとき平均変化率は
\(\displaystyle \frac{f(b)-f(a)}{b-a}=\frac{f(a+h)-f(a)}{\color{red}{h}}\)
と書き換えることができます。
ここで \( x\) の増分を限りなく0に近づけるときの極限を考えてみましょう。
つまり
\( \displaystyle \lim_{h \to 0} \displaystyle \frac{f(a+h)-f(a)}{h}\)
この極限値が存在する場合、
⇒ 極限値とは(数学Ⅱ:収束と無限大への発散と不定形について)
その値を
\(x=a\) における \( f(x)\) の「微分係数」といいます。
この微分係数は \( f'(x)\) という記号を使って表します。
\( y=f(x)\) と表すことも多いので分かっているとは思いますが、
\( \color{red}{y’}\) と表しているのも微分係数のことですよ。
【微分係数の定義】
関数 \( y=f(x)\) の \( x=a\) における微分係数とは
\( \displaystyle f'(a)=\lim_{h \to 0} \displaystyle \frac{f(a+h)-f(a)}{h}\)
である。
もちろんこの定義の式は \( x=a+h\) とおくことで
\( \displaystyle f'(a)=\lim_{x \to a} \displaystyle \frac{f(x)-f(a)}{x-a}\)
と書くことができます。
ただし、整関数においては任意の点で微分係数は存在するので、極限値があるとかないとかは考えなくて良いです。
この定義は覚えておいた方が良いですが、後に出てくる定理を覚えて使えば微分係数は簡単に求まりますので難しく感じるのであれば後回しにして良いですよ。
導関数
関数 \( y=f(x)\) が与えられていて、
\( x\) の1つ \( a\) に対し微分係数 \( f'(a)\) があります。
この \( a\) をいろいろとかえるとそれに対して \( f'(a)\) も変わります。
これらを集めると1つの関数となり、
その関数を \( f'(x)\) と表し、
関数 \( f(x)\) の導関数といいます。
【導関数の定義】
関数 \( f(x)\) の導関数とは
\( \displaystyle f'(x)=\lim_{h \to 0}{\displaystyle \frac{f(x+h)-f(x)}{h}}\)
で定められる関数である。
定数 \( a\) に対する微分係数を一般的にしたものと考えてください。
この関数 \( f(x)\) の導関数 \( f'(x)\) を求めることを「微分する」といいます。
微分を意味する記号は1つではありません。
余り見かけませんがいくつか紹介しておきます。
関数 \(f(x)\) の導関数 \( f'(x)\) は
\(\displaystyle y’ , \frac{dy}{dx} , \frac{df(x)}{dx} , \frac{d}{dx}f(x)\)
などと表されることがありますが、
数学\(\,Ⅱ\,\)の範囲では \( f'(x) , y’\) だけだと考えていて良いです。
定理を覚えてからはやる気になれないと思うので、
ここで定義にしたがって導関数を求めておきます。
定義にしたがって次の関数の導関数を求めよ。
(1) \( y=x^2\)
(2) \( y=x^3\)
(3) \(\displaystyle y=\frac{1}{x}\)
(4) \( y=\sqrt{x}\)
後に出てくる定理を使うと(1)(2)は簡単に求まります。
定理で微分ができるようになることが先で良いです。
(3)(4)は範囲外で定義にしたがって微分するしかありません。
定義に戻れば範囲外の関数も微分できるんですよ。
もう一度定義の式を書いておきますね。
\(\hspace{10pt}\displaystyle y’=f'(x)=\lim_{h \to 0}{\displaystyle \frac{f(x+h)-f(x)}{h}}\)
ですよ。
教科書などは一挙に計算しますが、ワケがわからなくなるので最初はやめておいた方が良いです。
部分的に計算して、最後に微分の定義の式に放り込む方が確実です。
(1) \( y=x^2\) なので
\(\hspace{10pt} f(x+h)=(x+h)^2=x^2+2hx+h^2\)
\(\hspace{10pt} f(x)=x^2\)
この問題はこれくらい書き出せば何とかなるでしょう。
\(\hspace{10pt} \displaystyle f'(x)=\lim_{h \to 0}{\displaystyle \frac{f(x+h)-f(x)}{h}}\\ \\
\displaystyle =\lim_{h \to 0}{\frac{(x^2+2hx+h^2)-(x^2)}{h}}\\ \\
\displaystyle =\lim_{h \to 0}{\frac{(2hx+h^2)}{h}}\\ \\
\displaystyle =\lim_{h \to 0}{(2x+h)}\\ \\
=2x\)
(2) \(y=x^3\)
\( y=f(x)\) とすると
\(\hspace{10pt} f(x+h)=(x+h)^3=x^3+3hx^2+3h^2x+h^3\)
\(\hspace{10pt} f(x)=x^3\)
導関数は
\(\hspace{10pt} \displaystyle f'(x)=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}\\ \\
\displaystyle =\lim_{h \to 0}{\frac{(x^3+3hx^2+3h^2x+h^3)-(x^3)}{h}}\\ \\
\displaystyle =\lim_{h \to 0}{\frac{(3hx^2+3h^2x+h^3)}{h}}\\ \\
\displaystyle =\lim_{h \to 0}{(3x^2+3hx+h^2)}\\ \\
=3x^2\)
(3) \(\displaystyle y=\frac{1}{x}\)
ここでは \( x \neq 0\) で考えます。
\( y=f(x)\) とすると
\(\hspace{10pt} f(x+h)=\displaystyle \frac{1}{(x+h)}\)
\(\hspace{10pt} f(x)=\displaystyle \frac{1}{x}\)
導関数は
\(\hspace{10pt} \displaystyle f'(x)=\lim_{h \to 0}{ \frac{f(x+h)-f(x)}{h}}\\ \\
\displaystyle =\lim_{h \to 0} {\frac{1}{h}\{f(x+h)-f(x)\}}\\ \\
\displaystyle =\lim_{h \to 0}{ \frac{1}{h} \left(\frac{1}{x+h}-\frac{1}{x}\right) }\\ \\
\displaystyle =\lim_{h \to 0}{ \frac{1}{h} \left( \frac{x-(x+h)}{x(x+h)}\right)} \\ \\
\displaystyle =\lim_{h \to 0}{ \frac{1}{h} \cdot \frac{-h}{x(x+h)}}\\ \\
\displaystyle =\lim_{h \to 0}{ \frac{-1}{x(x+h)}}\\ \\
=-\displaystyle \frac{1}{x^2}\)
(4) \( y=\sqrt{x}\)
関数を \( y=f(x)\) とすると
\(\hspace{10pt} f(x+h)=\sqrt{x+h}\)
\(\hspace{10pt} f(x)=\sqrt{x}\)
導関数は
\(\hspace{10pt} \displaystyle f'(x)=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}\\ \\
\displaystyle =\lim_{h \to 0}{\frac{ (\sqrt{x+h})-(\sqrt{x}) }{h}}\)
ここで極限では良く使う手法「分子の有理化」を行います。
\(\hspace{10pt} \displaystyle \lim_{h \to 0}{\frac{ (\sqrt{x+h})-(\sqrt{x}) }{h}}\\ \\
\displaystyle =\lim_{h \to 0}{\frac{ \sqrt{x+h}-\sqrt{x} }{h}}\\ \\
\displaystyle =\lim_{h \to 0}{\frac{(\sqrt{x+h}-\sqrt{x}) (\sqrt{x+h}+\sqrt{x}) }{ h (\sqrt{x+h}+\sqrt{x}) }}\\
\displaystyle =\lim_{h \to 0}{ \frac{ (x+h)-(x) }{h (\sqrt{x+h}+\sqrt{x}) } }\\ \\
\displaystyle =\lim_{h \to 0}{ \frac{ h }{h (\sqrt{x+h}+\sqrt{x}) } }\\ \\
\displaystyle =\lim_{h \to 0}{ \frac{ 1 }{ \sqrt{x+h}+\sqrt{x} } }\\ \\
\displaystyle =\lim_{h \to 0}{ \frac{ 1 }{ \sqrt{x}+\sqrt{x} } }\hspace{7pt} =\hspace{7pt}\underline{ \frac{1}{2\sqrt{x}} }\)
定義による微分も飽きてきたでしょうから定理に入ります。
ただ、この定義は覚えておいた方が良いですよ。
微分の公式
微分の定義にしたがった導関数は求められるようになりましたが、
定理から微分するのが普通です。
証明は定義にしたがって計算すればできるので省略します。
【定理1】 定数関数の導関数
定数 \( c\) において \( (c)’=0\)
書き方を変えると \(\displaystyle \frac{d}{dx}c=0\) である。
定数は微分すると0になるということです。
\( y\) の導関数を \( y’\) のように表すのと同じで、
各項 \( ax^n\) の導関数を \( (ax^n)’\) と表すことは説明不要でしょう。
まだあります。
【定理2】
\( m\) が正の整数のとき \( (x^m)’=mx^{m-1}\)
書き方を変えると \(\displaystyle \frac{d}{dx}x^m=mx^{m-1}\) である。
これが普通に使われる微分です。
整関数の範囲で微分するので \( m\) を正の整数と限定しています。
例えば、
\( (x^\color{red}{2})’=\color{red}{2}x\)
\( (x^\color{red}{3})’=\color{red}{3}x^2\)
と微分できるということです。
\(m=0\) のときは\((x^m)\)は定数になるので定理1が使えるので微分すると0になります。
さらに \( m\) が負の整数のときも成り立ちます。
【定理3】
\( m\) が負の整数のとき \( (x^m)’=mx^{m-1}\)
書き方を変えて \(\displaystyle \frac{d}{dx}x^m=mx^{m-1}\)
ただし、\( x \neq 0\) である。
これって \( x \neq 0\) という条件はありますが、\( m\) が正の数のときと同じに見えますよね。
同じなんです。
例えば、
\( y=\displaystyle \frac{1}{x}\)
を微分すると
\(\begin{eqnarray}\displaystyle
y’&=&\left(\displaystyle \frac{1}{x}\right)’\\
&=&(x^{-1})’\\
&=&(-1)x^{-2}\\
&=&-\frac{1}{x^2}
\end{eqnarray}\)
となり例題1(3)と同じ結果です。
この公式は整数だけに限らず有理数でも無理数でも成り立つ公式ですが範囲外なので説明しません。
数学\(\,Ⅲ\,\)で詳しく学んでください。
もう一つだけ定理を加えておきます。
これでひっかかる高校生は見たことありませんが一応定理なのであげておきます。
微分の線型性です。
「線型性という言葉はどうでも良い」ので定理自体は理解しておいてください。
要は「足した後微分しても」、「微分した後足しても」同じ結果ですよ、ということです。
【定理】微分の線型性
関数 \( f(x) , g(x)\) が微分可能なとき
ⅰ) \(\displaystyle \left\{cf(x)\right\}’=c\left\{f(x)\right\}’\)
\(c\) は定数です。
ⅱ)
\(\displaystyle \left\{f(x)+g(x)\right\}’=\left\{f(x)\right\}’+\left\{g(x)\right\}’\)
\(\displaystyle \left\{f(x)-g(x)\right\}’=\left\{f(x)\right\}’-\left\{g(x)\right\}’\)
難しく見ないでください。
\(\hspace{10pt} y=x^3-3x^2+4x+5\)
があるとき
\(\hspace{10pt} y’=(x^3)’-3(x^2)’+4(x)’+(5)’\\ \\
=3x^2-3(2x)+4(1)+0\\ \\
=3x^2-6x+4\)
のように「足し算」と「引き算」においては部分的に微分して良いということで、
暗算レベルで計算できるようになったということです。
(掛け算、割り算はダメです。)
この公式(定理)を知ったら定義にしたがった微分は嫌になりますが、問題の作成者は「定義覚えてますか?」という意味で出題することがありますので、
「定義にしたがった微分」も忘れないでください。
数学\(\,Ⅲ\,\)での微分積分はもっと広い範囲で微分しますが、数学\(\,Ⅱ\,\)ではここまでで良いのです。
これから接線や極値などいろいろな問題を解いて行くことになりますが、ここから始まると考えておいてください。
本当なら極限値も含めて説明すべきなのですが、
公式が使えるようになってからでも遅くはないだろうということで別にしてあります。
(連続性や微分可能性や極限値は数学\(\,Ⅲ\,\)で詳しくやってください。)
⇒ 極限値とは(数学Ⅱ:収束と無限大への発散と不定形について)
意味を知れば簡単なので、用語の確認をしておいてください。
微分法積分法の(応用を少し除いて)ほとんどはここで確認できます。