数学Ⅱの範囲内での極限値を求める問題を解く以前の説明です。
収束、発散、無限大、不定形、この言葉だけでもお伝えしておきます。
数学Ⅲの内容に触れずに極限値を求めようとする困難な部分が出てきますし、
定義や定理を詳しく説明すると長くなりますし、必要無い人にとっては意味なく時間をつぶします。
なのでここでは言葉だけでも覚えて問題に当たれるようにしておきます。
極限値とは
極限値の定義を簡単に済ませます。
【極限値の定義】
関数 \( y=f(x)\) において
\(x\) が限りなく \( a\) に近づくとき、
\(f(x)\) が一定の値 \( A\) に近づくならば、
\( A\) を \( x\) が \(a\) に近づくときの『極限値』という。
または、
\( x\) が \( a\) に近づくとき、
\( f(x)\) は \(A\) に『収束する』という。
極限を表すとき、
\( x\,\rightarrow \,a\) のとき \( f(x) \,\rightarrow \,A\)
と表すこともありますが、
\( \displaystyle \color{red}{\lim_{x \to a} f(x)=A}\)
と表すことが多いです。
誤解してはいけないのは、
\( f(a)=A\)
であるとは「限らない」ということです。
限りなく近づく、ということと同じ値とは違います。
ここを説明するのがややこしいので数学\(\,Ⅱ\,\)で極限値には触れたくないのですが、
極限値とはその値に限りなく近づく、ということです。
「極限値」という言葉だけでも覚えておいてください。
ついでに、
問題を解いて行く上で都合が良いように、言葉をいくつか足しておきます。
発散と無限大と不定形
数学\(\,Ⅲ\,\)を学ぶ人にとっては最初に習得しなくてはならない知識ですが、
数学\(\,Ⅱ\,\)においては何となくで良いので分かった気になっておいてください。
例えば、
関数 \(\displaystyle y=\frac{1}{x}\)
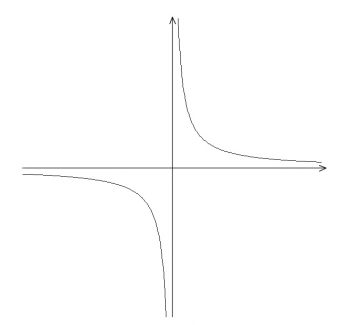
において \( x \rightarrow 0\) とすると極限値は存在しません。
限りなく正の(+)の大きい値なのか
限りなく負の(-)の小さい値なのかすら分かりません。
このように極限値が存在しない(収束しない)ときは「発散する」といいます。
発散にもいろいろあるのですが数学\(\,Ⅲ\,\)でであいましょう。
とにかく極限値が存在しない場合をすべて「発散」といいます。
つまり、極限には「収束」か「発散」」しか無いということです。
無限大とは
関数 \( y=f(x)\) において
\( x\) が限りなく \( a\) に近づくとき
関数の値 \( f(x)\) が限りなく大きくなるならば、
\( f(x)\) は収束はせず、「正の無限大に発散する」といいます。
「無限大」は記号で「 \( \color{green}{\infty}\) 」と表しますので、
\( \displaystyle \lim_{x \to a} f(x)=+\infty\)
となりますが \( \infty\) は値(数)ではありませんので収束しているのではなく発散しているのです。
数ではないので \( \infty-\infty=0\) などの計算もできません。
また、
逆に関数 \( y=f(x)\) において
\( x\) が限りなく \( a\) に近づくとき
関数の値 \( f(x)\) が限りなく小さくなるならば、
\( f(x)\) は収束はせず、「負の無限大に発散する」といいます。
\( \displaystyle \lim_{x \to a} f(x)=-\infty\)
「負の無限大」は小さいからといって「無限小」とはいいませんので注意してください。
「無限小」は意味が違ってきます。
極限と無限大になる発散はだいたいでも良いのでイメージできたでしょうか。
次は計算問題を解く解きに説明が簡単に済むので説明を加えておきたいものです。
不定形の極限
微分であつかう極限の形には分数の形の関数をあつかうことが多くなります。
数学\(\,Ⅱ\,\)においては有理関数ですが、
\( \displaystyle \lim_{x \to a} \,\displaystyle \frac{f(x)}{g(x)}\)
といった形です。
具体的には、
\( \displaystyle \lim_{x \to 1} \displaystyle \frac{x^2+x-2}{x-1}\)
などのような極限です。
このとき、
\( \displaystyle \lim_{x \to a} \,f(x)=\mathrm{\alpha} \)
\( \displaystyle \lim_{x \to a} \,g(x)=\mathrm{\beta}\)
がともに存在するなら
\( \mathrm{\alpha \neq 0\hspace{7pt},\hspace{7pt}\beta \neq 0}\)
の場合、
\( \displaystyle \lim_{x \to a} \,\displaystyle \frac{f(x)}{g(x)}=\mathrm{\displaystyle \frac{\alpha}{\beta}}\)
としてかまいません。
これは定理としてあります。
これは \( \mathrm{\alpha=0}\) のときにもあてはまります。
ところが、\( \,\mathrm{\beta=0}\,\)の場合はちょっと違ってきます。
\( \mathrm{\color{red}{\alpha\neq 0}}\) の場合
分子の \(f(x)\) はある定数に収束しますが、
分母の \( g(x)\) は0に近づくことになるので
\(\displaystyle \frac{f(x)}{g(x)}\) の値は正か負の無限大になります。
つまりは発散するということです。
\( \mathrm{\color{red}{\alpha=0}}\) の場合
分子の \( f(x)\) は0収束しますが、
分母の \( g(x)\) も0に近づくことになるので
\(\displaystyle \lim_{x \to a} \frac{f(x)}{g(x)}=\frac{\color{red}{0}}{\color{red}{0}}\)
となりますがこんな形の数はありません。
これを『不定形の極限』といいます。
不定形の極限が存在するかどうかは場合によって変わってきます。
ここも説明すると長くなるので、数学\(\,Ⅱ\,\)に限っていうと、存在します。
無限大が定義されていないので当然ですが、ちょっと直感を働かせてみませんか?
次の極限が収束するか発散するか直感的に答えよ。
\(\displaystyle \frac{3}{\infty} , \frac{0}{\infty} , \frac{3}{0} , \frac{0}{0} , \frac{\infty}{\infty} , \frac{\infty}{0}\)
ちょっと問題の出し方がへん?だけど何となく理解してくださいね。笑
正の数だけで表していますが負の数が混じっても同じです。
\(\displaystyle \frac{3}{\infty} , \frac{0}{\infty} , \frac{3}{0} , \frac{\infty}{0}\)
は0に収束するかか、無限大に発散するかのどちらかです。
しかし、
\(\displaystyle \frac{0}{0} , \frac{\infty}{\infty}\)
については分かりません。
この分からない形が不定形です。
この形をあつかうことがテーマの1つにあるのですが、数学\(\,Ⅲ\,\)を学ぶときもこの直感的な感覚は持っておいてください。
大学で学ぶ数学との中間に位置する数学\(\,Ⅲ\,\)では直感に頼るところも出てきますからね。
とにかく、
極限が存在するかどうか分からないときを不定形という約束をして問題演習に行きましょう。
数学\(\,Ⅱ\,\)の極限は簡単ですなのでここはさらっと通り過ぎて良いですよ。笑
ちょっとした技をお伝えしますので、答は簡単に出せるようになりますよ。
入試におぴて微分法は積分法とまとめて質問されることが普通です。