面積を求める問題の求め方はいろいろとありますが、定積分もその１つです。
関数で「囲まれる」面積を求める問題はすべてが定積分を使うといって良いでしょう。
ここでは定積分を使って面積を求める基本問題の解き方とちょっと便利な公式を２つだけ紹介しておきます。
定積分と面積
定積分は関数ではなく「値」ですが面積そのものではありません。
しかし、計算方法によっては面積にかえることができます。
細かいことを言い出すとキリがないので簡単に説明すると、
（大学での内容にまで話が及ぶのでややこしくて参考にならなくなる）
定積分
\(\hspace{10pt} \displaystyle \int_{-1}^1 2x dx\\ \\
\displaystyle =\left[x^2\right]_{-1}^1\\ \\
=(1)^2-(-1)^2\,=0 \)
ですが
\(\hspace{10pt}\displaystyle \int_{-1}^0 (-2x) dx +\int_{0}^1 (2x) dx \\ \\
\displaystyle =\left[-x^2\right]_{-1}^0 + \left[x^2\right]_{0}^1\\ \\
\displaystyle =\left\{0-(-1)^2\right\}+\left\{(1)^2-(0)^2\right\}=2\)
とするとこれは
\( y=2x\) と \( x\)軸と直線 \( x=-1\,,\,1\) で囲まれる面積
になります。
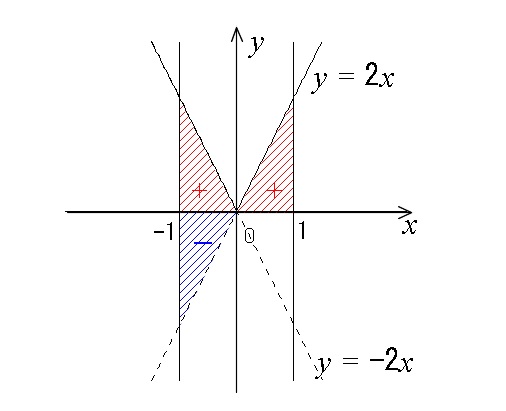
定積分で面積を求めたかったら、
「グラフを \( x\) 軸で折り返して正の部分の関数で定積分すれば面積になる」
ということなのですが、言い換えると
\(\hspace{10pt} \displaystyle \int_a^b \color{red}{|f(x)|}dx\)
が面積を表します。
絶対値のついた関数を見る時はグラフを参考にしますよね？
同じように面積でもグラフは重要になってきますよ。
問題に入りましょう。
\( f(x)=x^2-2x-3\) のグラフと直線 \( y=12\) で囲まれる部分の面積を求めよ。
また、
\( g(x)=|x^2-2x-3|\) のグラフと直線 \( y=12\) で囲まれる部分の面積を求めよ。
どちらも面積ですが、違いは像像できますよね？
絶対値のついたグラフは \( x\) 軸で折り返されるので変な形になるかもしれません。
繰り返しになりますが面積の定義は、数学\(\,Ⅲ\,\)もしくは大学の数学に先送りします。
（簡単に言えば、線分の積み重ねです。）
曲線で囲む面積の求め方
小学校、中学校のときに長方形、三角形、円などの面積は公式で求めていましたが意味は考えず求めていました。
ここでも同じようにどうすれば面積が求まるかを説明します。
２つの曲線を表す関数があってそれらの「２曲線で囲まれる面積」は、
グラフで（「上になる関数」－「下になる関数」）を交点から交点まで定積分。
これが簡単な面積の公式となります。
関数 \( f(x)\,,\,g(x)\) が
区間 \( a≦ b\) では \( \color{blue}{f(x)}\) が上、
区間 \( b≦ c\) では \( \color{red}{g(x)}\) が上、
という場合は、
\(\hspace{10pt} \displaystyle S=\int_a^b \left(\color{blue}{f(x)}-\color{red}{g(x)}\right)dx + \int_b^c \left(\color{blue}{g(x)}-\color{red}{f(x)}\right)dx\)
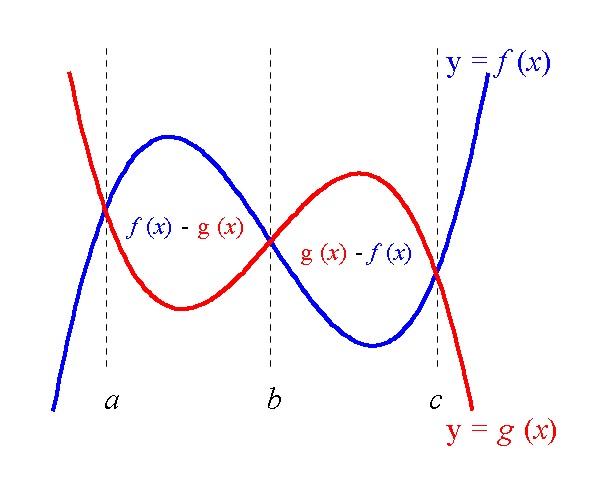
積分区間となる直線で囲む場合も同じです。
グラフで「\(\color{red}{（上になる関数）-（下になる関数）}\)」を定積分。
何故かというと、面積は線分の積み重ねというのを先に書きました。
線分とは長さのことなので負の数(－)にはなりません。
だから上の曲線から下の曲線を引いておかなければ正にならないから、
面積としてマイナス(－)となってしまうのです。
定積分は正負関係なしに計算するので「（定積分）＝（面積）とならない」理由です。
ややこしい関数に関しては数学\(\,Ⅲ\,\)でやりますからここでは例題に沿って説明します。
関数 \( f(x)=x^2-2x-3\)
と
直線 \( y=12\)
の２つは、
\( \hspace{10pt}x^2-2x-3=12\\
\Leftrightarrow \hspace{5pt} x^2-2x-15=0\\
\Leftrightarrow \hspace{5pt} (x-5)(x+3)=0\)
から交点を出して、図のようになります。
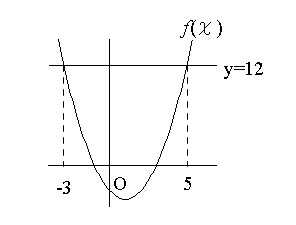
\( -3≦ x ≦ 5\) において \( y=12\) が上（同じ点を含む）になります。
よって、２つの曲線で囲まれる面積は、
\(\hspace{10pt} \displaystyle \int_{-3}^5\left\{(12)-(x^2-2x-3)\right\}dx\)
を計算すれば良いのです。
定積分自体は簡単で、
\(\hspace{10pt} \displaystyle \int_{-3}^5\left\{(12)-(x^2-2x-3)\right\}dx\\
\displaystyle =\int_{-3}^5 (-x^2+2x+15)dx\\
\displaystyle =\left[-\frac{1}{3}x^3+x^2+15x\right]_{-3}^5\\
\displaystyle =\underline{ \color{red}{\frac{256}{3}} }\)
この定積分は公式利用して
\(\hspace{10pt} \displaystyle \int_{-3}^5 (-x^2+2x+15)dx\\ \\
\displaystyle =-\int_{-3}^5 (x+3)(x-5)dx\\ \\
\displaystyle =\frac{1}{6}\cdot (5+3)^3=\underline{ \color{red}{\frac{256}{3}} }\)
でいいですよ。
絶対値のついた関数の定積分
後半です。
前半との違いは、絶対値がついているか、いないかだけです。
\(\, g(x)=|x^2-2x-3|\,\)のグラフは、
\(\, y=12\,\)とともに図示すると図のようになります。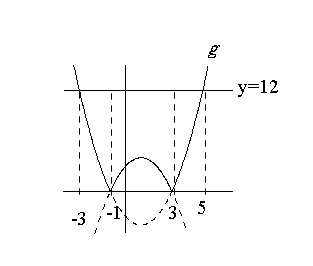
上になるのは\(\, y=12\,\)で同じですが、
\( g(x)=|x^2-2x-3|\) は
区間\(\,-1\,≦\,x\,≦\,3\,\)で上に凸
となるので、積分区間を分けて定積分します。
\( g(x)=|x^2-2x-3|\,\)は、
\( x≦ -1\,,\,3≦ x\) で \( g(x)=x^2-2x-3\)
\( -1≦x ≦ 3\) で \( g(x)=-(x^2-2x-3)\)
よって２つの曲線で囲まれる面積 \( S\) は、
\(\hspace{10pt} \displaystyle S=\int_{-3}^{-1}\left\{(12)-(x^2-2x-3)\right\}dx\\ \\
\displaystyle \hspace{30pt}+\int_{-1}^3 \left\{(12)+(x^2-2x-3)\right\}dx\\ \\
\displaystyle \hspace{40pt}+\int_{3}^5 \left\{(12)-(x^2-2x-3)\right\}dx\)
となります。
ここで計算しても良いのですがもう少し図とにらめっこすると、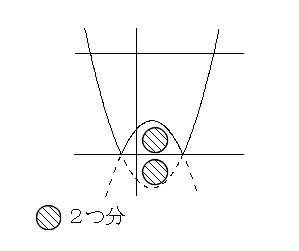
上に凸になっている部分２つ分が例題の前半より少なくなっているので、
凸部分の下の直線が\(\,y=0\,\)（\(\,x\,\) 軸）であることに注意して、
2つの凸部分だけを先に計算すると、
\(\hspace{10pt}\displaystyle 2\times \int_{-1}^3\left\{(0)-(x^2-2x-3)\right\}dx\\
\displaystyle =2\int_{-1}^3\left\{-(x^2-2x-3)\right\}dx \\
\displaystyle =2\underline{\int_{-1}^3\left\{-(x+1)(x-3)\right\}dx}\\
\displaystyle =2\cdot \underline{\frac{1}{6}(3+1)^3}\\
\displaystyle =\color{blue}{\frac{64}{3}}\)
前半の、放物線と直線とで囲まれる面積から求める面積\(\,Sは\,\)
\(\begin{eqnarray}\displaystyle S&=&\color{red}{\frac{256}{3}}-\color{blue}{\frac{64}{3}}\\
&=&\frac{192}{3}\\
&=&\underline{ 64 }
\end{eqnarray}\)
とした方がはやそうですよ。
面積計算に便利な公式
下線部分の計算には
\(\hspace{10pt} \color{red}{\displaystyle \int_{\alpha}^{\beta}(x-\alpha)(x-\beta)=-\displaystyle \frac{1}{6}(\beta-\alpha)^3}\)
を使っています。
もちろん普通に定積分しても同じ結果ですが、証明なしに使って良いのでこの公式だけは覚えておくと良いです。
他にも公式はいくつもあります。
接線と曲線と直線で囲む面積なども公式としてはありますが覚えなくて良いです。
むしろ公式にたよると共通テスト（センター試験）やマーク式の問題では誘導部分を埋めなくてはならないので苦労します。
１つだけ追加して覚えておくと良い公式を紹介しておきます。
３次関数とその接線とで囲まれる面積の公式です。
無理に覚えなくて良いですよ。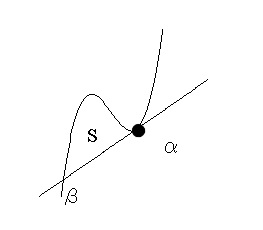
３次関数と直線（接線）の交点が、１つが重解で２つになる場合ですが、
その２つを \( \alpha\,,\,\beta\) とすると、
囲まれる面積は
\(\hspace{10pt} \color{red}{\displaystyle \int_{\alpha}^{\beta} a(x-\alpha)^2(x-\beta)dx=\frac{|a|}{12}(\beta-\alpha)^4}\)
（ \( |a|\) の \( a\) は３次の係数です。）
となります。使って良いですよ。
接線なので１つは重解であることをお忘れなく。
２次関数の場合は２つの解は実数であれば使えますが、３次関数の公式は重解を持つ場合のみです。
接線が出てきたら使えます。
２本の接線と放物線とで囲む面積の公式もあります。
別のところで紹介していますがあれは覚えなくて良いです。
センター（共通テスト）では基本通りの作業をするかどうかが問われることが多いです。
個人的には「使える公式は使おう！」って考えてますけど、
裏技的な方法を使って何でも楽すれば良いのではありません。
（この程度は普通に教科書にあってもおかしくないので裏技とはいいませんけど。）
面積を求めるとき、
「上の関数から下の関数を引いて定積分」
これを徹底してください。
面積を求める問題は微分積分には必ずといって良いほどついてきます。
いろいろな問題がありますが、基本的には同じですよ。
では、公式として覚えなくて良いけど、解けた方がいい問題をやっておきましょう。
積分区間を分ける面積計算ですが、これが普通です。
面積を求めるにはグラフがあった方が良いですが、それは微分からつながっています。