曲線に引いた2本の接線と曲線とで囲まれる面積を定積分で求める問題の解き方です。
ほとんどの問題では接線を求めた後面積を求めるという誘導になります。
接線を求める微分の段階と、面積計算ができるかという積分との二段階の問題になりますので微分積分分野ではよくでる形の問題です。
積分で面積を求めるときやるべきこと
接線、定積分両方を復習することになります。
融合とはいえませんが、微分積分の基本の確認問題です。
点\(\,(\,1\,,\,-3\,)\,\)を通って曲線 \( C:y=x^2\) に\(\,2\,\)本の接線を引く。
接線の方程式を求めよ。
また、この\(\,2\,\)本の接線と曲線\( \,C\,\)とで囲まれる面積を求めよ。
最初にするべきことはグラフの概形を見ておくことです。
だいたいで良いので位置関係を見ておくことで問題の難易度はかなり変わりますよ。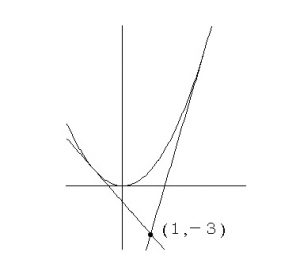
先に接線を求めますが、「接線」といえば?
「接点の設定」ですね。
接点を\(\,(\, \color{red}{t}\,,\,\color{red}{t^2}\,)\,\)とおくと
\( y=x^2\) より \( y’=2x\)
となるので接線の方程式は
\( y-\color{red}{t^2}=\color{red}{2t}(x-\color{red}{t})\) ・・・①
とおけます。
これが点\(\,(\,1\,,\,-3\,)\,\)を通るので、①に代入して、
\(\hspace{10pt} -3-t^2=2t(1-t)\\ \\
\Leftrightarrow \hspace{5pt} -3-t^2=2t-2t^2\\ \\
\Leftrightarrow \hspace{5pt} t^2-2t-3=0\\ \\
\Leftrightarrow \hspace{5pt} (t+1)(t-3)=0\\ \\
\Leftrightarrow \hspace{5pt} t=-1\,,\,3\)
よって接線の方程式は①から
\( y=-2x-1\) と \( y=6x-9\)
ここまでは微分でおきまりの接線問題なので大丈夫でしょう。
後は、区間に気をつけて積分するだけです。
接点が分かったので図を見てみると、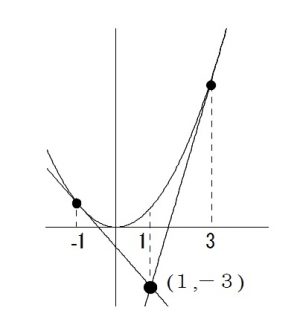
上になっている関数は同じですが、
下の直線が違っているので積分区間が分かれることが分かります。
積分区間は \( [\,-1\,,\,1\,]\) と \( [\,1\,,\,3\,]\) とに分かれます。
\(-1\,≦\,x\,≦\, 1\,\)では\(\,y=x^2\,\) が上にあり、\(\,y=-2x-1\,\)が下
\(1\,≦\,x\,≦\,3\,\)では\(\,y=x^2\,\)が上にあり、\(\,y=6x-9\,\)が下
となっています。
とにかく面積を求めるときは、
「上の関数から下の関数を引いて定積分」
すればでます。
問題によっては積分区間が細かく、上下が微妙なものもあるのでグラフは大きめに書くのがコツとなります。
積分区間が細かいというより、全体に対する部分的な位置関係が比較的小さいといった方が良いでしょうか。
部分的に拡大して書くと分かりやすいことがありますよ。
求める面積は
\(\hspace{10pt} \displaystyle \int_{-1}^1\{x^2-(-2x-1)\}dx + \int_{1}^{3} \{x^2-(6x-9)\}dx\\ \\
\displaystyle =\int_{-1}^1 (x^2+2x+1)dx + \int_{1}^{3} (x^2-6x+9)dx\\ \\
\displaystyle =\int_{-1}^1 (x^2+1)dx + \int_{1}^{3} (x^2-6x+9)dx\\ \\
\displaystyle =2\int_{0}^1 (x^2+1)dx + \int_{1}^{3} (x^2-6x+9)dx\\ \\
\displaystyle =2\left[\frac{1}{3}x^3+x\right]_{0}^{1}+\left[\frac{1}{3}x^3-3x^2+9x\right]_{1}^{3}\\ \\
\displaystyle =2\left(\frac{1}{3}+1\right)+\frac{1}{3}\left(3^3-1^3\right)-3\left(3^2-1^2\right)+9(3-1)\\ \\
\displaystyle =\frac{8}{3}+\frac{26}{3}-24+18\\ \\
\displaystyle =\frac{34}{3}-6=\frac{16}{3}\)
この定積分では
\( f(x)\) が偶関数なら
\(\hspace{10pt}\displaystyle \int_{-a}^{a} f(x)dx=2\int_0^a f(x)dx\)
\( f(x)\) が奇関数なら
\(\hspace{10pt} \displaystyle \int_{-a}^{a} f(x)dx=0\)
という公式は使いましたが普通に定積分しました。
これで良いです。
2本の接線と放物線で囲まれる面積の公式
\(\,2\,\)本の接線と放物線との間には公式が存在します。
\( y=ax^2+bx+c\,\)と点\(\,(\,p\,,\,q\,)\,\)から引いた接線において、
接点の\(\,x\,\)座標を\(\,\alpha \,,\,\beta \,\)とすると
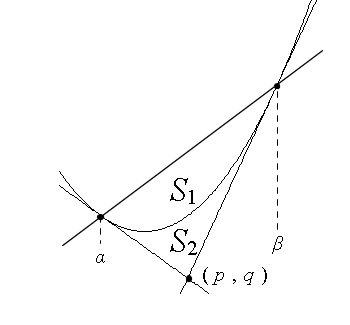
点\(\,(\,p\,,\,q\,)\,\)の\(\,x\,\)座標\(\, p\,\)は
\(\hspace{10pt} p=\displaystyle \frac{\alpha+\beta}{2}\)
であり、
( \(\,x\,\)座標は2つの接点の中間になるということです。)
\(\,2\,\)本の接線と放物線で囲まれた図の \(\color{red}{S_2}\) の面積は
\(\hspace{10pt} \color{red}{S_2=\displaystyle \frac{|a|}{12}(\beta-\alpha)^3}\)
となります。
2つの接点\(\,\alpha \,,\,\beta \,\)を通る直線と放物線で囲まれる面積\(\,\color{blue}{S_1}\,\)は
\( \hspace{10pt}\color{blue}{S_1=\displaystyle \frac{|a|}{6}(\beta-\alpha)^3}\)
となることは有名ですよね。
したがって\(\, \color{blue}{S_1}:\color{red}{S_2}\,=\,\color{blue}{2}:\color{red}{1}\,\)も言えます。
しかし、こんなことは覚えなくて良いです。
普通に定積分してください。
余裕が持てるようになって検算に使うなら良いですが、最初からこの方法を取ろうとすると取れる点も取れなくなりますよ。
どんな場合でも面積を線分の積み重ねと考えるので、面積を求めるときは
「上になっている関数から、下になっている関数を引いて定積分」
それで面積は求まります。
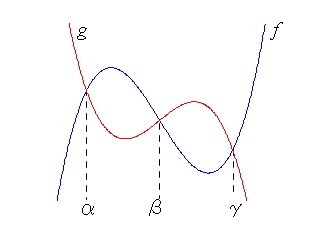
図の2つの3次関数 \( \color{blue}{f}\) と \( \color{red}{g}\) で囲まれる面積は、
\( \hspace{10pt}\displaystyle \int_{\alpha}^{\beta}(\,\color{blue}{f}-\color{red}{g}\,)dx \hspace{7pt}+ \hspace{7pt}\int_{\beta}^{\gamma}(\,\color{red}{g}-\color{blue}{f}\,)dx \)
です。
基本通りで十分なのです。
面積が求められるようになったところで、
これで微分積分の基本とちょっとした応用力は身についていますよ。