トレミーの定理は中学の図形(相似)を使って証明できますが、三角比の余弦定理を使うと計算だけで証明できます。
円に内接する四角形における定理なので幾何の性質と三角比を使いこなせれば必要無い定理ですが、高校生向けに示しておきます。
数学が苦手な受験生には、この定理を証明する前にやっておくことはたくさんありますよ。
トレミーの定理
定理を確認しておきます。
【トレミーの定理】
円に内接する四角形ABCDにおいて、
対辺の長さの和は対角線の長さの積に等しい。
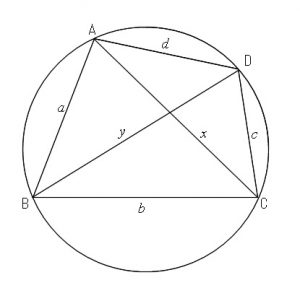
すなわち、
\(AB=d\,,\,BC=b\,,\,CD=c\,,\,DA=d\)
とし、\(AC=x\,,\,BD=y\) とすると
\(\color{red}{\large{ac+bd=xy}}\)
である。
中学の図形の「相似」を利用した証明は
⇒ 中学生ができるトレミーの定理の証明方法
余弦定理を使った証明
ここでは余弦定理を使って証明しておきます。
△ABCに余弦定理を使うと、
\(x^2=a^2+b^2-2ab\cos B ・・・①\)
同様に△ADCで
\(x^2=c^2+d^2-2cd\cos D\)
四角形ABCDが円に内接していることから
内対角において \(\angle B+\angle D=180^{\circ}\) だから
\(x^2=c^2+d^2-2cd\cos D\\ \\
\hspace{10pt}=c^2+d^2\color{red}{-2cd\cos (180^{\circ}-B)}\\ \\
\hspace{10pt}=c^2+d^2\color{red}{+2cd\cos B} ・・・②\)
ここで \(\cos B\) を消去しておきたいのですが、
分数にするのは嫌なので、(好きな人は分数にして良いですよ。)
①に\(cd\)、②に\(ab\)をかけて
\(cdx^2=cd(a^2+b^2)-2abcd\cos B ・・・①’\)
\(abx^2=ab(c^2+d^2)+2abcd\cos B ・・・②’\)
両辺を足すと
\((\color{green}{cd+ab})x^2=cd(a^2+b^2)+ab(c^2+d^2)\\ \\
\hspace{50pt}=cda^2+cdb^2+abc^2+abd^2\\ \\
\hspace{50pt}=cda^2+(bc^2+bd^2)a+b^2cd\\ \\
\hspace{50pt}=(\color{red}{ac+bd})(\color{blue}{ad+bc}) ・・・③\)
この右辺の因数分解は後で処理しても良いのですが、
\(ac+bd\) を見ておきたかったので先にしました。笑
続けて△ABDで
\(y^2=a^2+d^2-2ad\cos A ・・・④\)
△CBDで
\(y^2=b^2+c^2-2bc\cos C\\ \\
\hspace{10pt}=b^2+c^2\color{red}{-2bc\cos (180^{\circ}-A)}\\ \\
\hspace{10pt}=b^2+c^2\color{red}{+2bc\cos A} ・・・⑤\)
④に\(bc\)、⑤に\(ad\)をかけて
\(bcy^2=bc(a^2+d^2)-2abcd\cos A ・・・④’\)
\(ady^2=ad(b^2+c^2)+2abcd\cos A ・・・⑤’\)
両辺を加えると
\((\color{blue}{bc+ad})y^2=bc(a^2+d^2)+ad(b^2+c^2)\\ \\
\hspace{50pt}=bca^2+bcd^2+adb^2+adc^2\\ \\
\hspace{50pt}=bca^2+(db^2+dc^2)a+bcd^2\\ \\
\hspace{50pt}=(\color{red}{ac+bd})(\color{green}{ab+cd}) ・・・⑥\)
⑤⑥の各辺どうしをかけると
\((\color{green}{cd+ab})(\color{blue}{bc+ad})x^2y^2=(\color{red}{ac+bd})^2(\color{green}{ad+bc})(\color{blue}{ab+cd})\\ \\
\Leftrightarrow x^2y^2=(\color{red}{ac+bd})^2\)
\(x\,>\,0 , y\,>\,0\) なので
\(xy=\color{red}{ac+bd}\) (証明終わり)
トレミーの定理は覚えて使って良いですが、
こっちが使いこなせることが先ですよ。