ベクトル分野で面積を求める問題は多いので公式をいくつかお伝えしておきます。
面積を求めるには三角比や正弦定理や余弦定理を利用し求める方法で良いのですが、
ベクトルの大きさと内積だけで求めることができる記憶に値する公式もあります。
また、ベクトルの大きさと内積と角度の関係も改めて確認しておきましょう。
三角形の面積をベクトルと三角比で表す公式
三角形の面積の公式は小学生の頃から知っています。
\(\,\color{red}{(三角形の面積)=(底辺)\times (高さ)\div 2}\,\)
これが一番分かり易いです。
中学になると文字を使って表します。
底辺を\(\,\color{red}{a}\,\)
高さを\(\,\color{blue}{h}\,\)
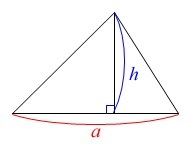とすると面積\(\,\mathrm{S}\,\)は
\(\hspace{10pt}\displaystyle \,\mathrm{S}=\frac{1}{2}\,\color{red}{a}\,\color{blue}{h}\,\)
三角比を用いた面積の求め方
高校になると表し方がいくつか出てきますが、
三角比では面積の公式として\(\,\mathrm{△ABC}\,\)の面積\(\,\mathrm{S}\,\)は
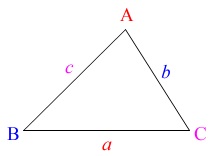
\(\begin{eqnarray}\displaystyle
\mathrm{S}&=&\frac{1}{2}\,\color{red}{a}\,\color{blue}{b}\,\sin \mathrm{\color{magenta}{C}}\\
&=&\frac{1}{2}\,\color{blue}{b}\,\color{magenta}{c}\,\sin \mathrm{\color{red}{A}}\\
&=&\frac{1}{2}\,\color{magenta}{c}\,\color{red}{a}\,\sin \mathrm{\color{blue}{B}}
\end{eqnarray}\)
高校生に向けてはカラフルになりすぎましたが、笑
頂点\(\,\mathrm{A}\,\)の対辺は\(\,a\,\)
頂点\(\,\mathrm{B}\,\)の対辺は\(\,b\,\)
などとするのは数学の慣習なので特に設定されていなければ読み取れるようにしておきましょう。
自分で設定する場合は
\(\,\mathrm{A}\,\)の対辺を\(\,a\,\)などとする。
と書いた方が良いですよ。
とそんな当たり前のことを説明したいのではありません。
三角比で、正弦定理、余弦定理、面積の公式を覚えていない人はいないと信じて先に進みます。
次はベクトルを用いた面積です。
ベクトルを用いた面積の求め方
ベクトルの大きさは長さを意味するので\(\,\mathrm{△OAB}\,\)の面積\(\,\mathrm{S}\,\)は
\(\displaystyle \color{red}{\mathrm{S}=\frac{1}{2}\,|\overrightarrow{\mathrm{OA}}|\,|\overrightarrow{\mathrm{OB}}|\,\sin ∠\mathrm{AOB}}\)
後々出てくるので
\(\overrightarrow{\mathrm{OA}}=\vec{a}\)
\(\overrightarrow{\mathrm{OB}}=\vec{b}\)
\(\,\mathrm{∠AOB=\theta}\,\)
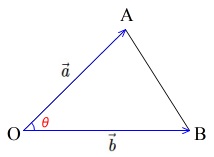としておきます。
改めて書き直すと
\(\displaystyle \color{red}{\mathrm{S}=\frac{1}{2}\,|\vec{a}|\,|\vec{b}|\,\sin \theta}\)
何故か？なんて理由より覚えて使ってもらいたい程度の公式ですが、
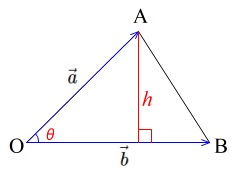\(\,\sin\,\)の定義から
\(\displaystyle \sin \theta=\frac{h}{\mathrm{OA}}\)
なので高さ\(\,h\,\)は
\(\begin{eqnarray}
\color{red}{h}&=&\mathrm{OA}\times \sin\theta\\
&=&\color{red}{|\vec{a}|\times \sin \theta}
\end{eqnarray}\)
が高さになるので、
小学生と同じように底辺\(\,|\vec{b}|\,\)と高さ\(\,h\,\)が分かれば同じ三角形の面積です。
平行四辺形の面積をベクトルで表す公式
平行四辺形は三角形2つ分の面積なので
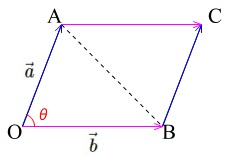三角形の面積を\(\,2\,\)倍すれば良いだけです。
\(\begin{eqnarray}
(平行四辺形\mathrm{OBCA})&=&2\times \frac{1}{2}\,|\vec{a}|\,|\vec{b}|\,\sin\theta\\
&=&\color{red}{|\vec{a}|\,|\vec{b}|\,\sin\theta}
\end{eqnarray}\)
当たり前のことですが覚えておきましょう。
別のところでもいずれ出会うでしょう。
（高校入試ですでに経験しているはずなのですが。）
本題は次の公式です。
教科書にもあるので一度見たことがあるかもしれませんが、覚えようとはしていないでしょう。笑
その1つです。
面積をベクトルの大きさと内積のみで表す記憶に値する公式
ここで紹介する公式は覚えなくても面積は先に出てきた公式で求めることができます。
なのに何故記憶に値する公式かというと、解答の時間短縮に非常に役立ち難関私立入試など計算量の非常に多い場合に役立つからです。
この後例題をお目にかけます。
では、三角比を使わずに面積を出す公式を導いておきます。
証明問題として出てもおかしくはない問題です。
では、三角比を使わずに面積を出す公式を導いておきます。
証明問題として出てもおかしくはない問題です。
泥くさい証明と、スマートな証明を示しておきます。笑
証明方法はどっちでも良いので使えるようになっておくと良いですね。
\(\,\mathrm{△OAB}\,\)の面積を\(\,\mathrm{S}\,\)とします。
\(\begin{eqnarray}\displaystyle
\mathrm{S}&=&\frac{1}{2}\,|\overrightarrow{\mathrm{OA}}|\,|\overrightarrow{\mathrm{OB}}|\,\sin ∠\mathrm{AOB}\\
&=&\frac{1}{2}\,|\vec{a}|\,|\vec{b}|\,\sin \theta
\end{eqnarray}\)
ここで\(\,\sin\theta\,\)をなくしたいのです。
そこで2つのことを思い出してください。
1つは内積の定義です。
\(\hspace{10pt}\vec{a}\cdot \vec{b}=|\vec{a}|\,|\vec{b}|\,\cos \theta ･･･①\)
もう一つは、三角比で大切な基本公式です。
\(\hspace{10pt}\sin^2\theta+\cos^2\theta=1 ･･･②\)
①の内積の定義から
\(\hspace{10pt}\displaystyle \cos \theta=\frac{\vec{a}\cdot \vec{b}}{|\vec{a}|\,|\vec{b}|}\)
②と面積の公式から\(\,\sin\theta\,\)を消したいので\(\,2\,\)乗します。
\(\hspace{10pt}\displaystyle \cos^2 \theta=\frac{(\,\vec{a}\cdot \vec{b}\,)^2}{(\,|\vec{a}|\,|\vec{b}|\,)^2}\)
②に代入すると
\(\begin{eqnarray}\displaystyle
\sin^2\theta+\cos^2\theta&=&1\\
\sin^2\theta&=&1-\cos^2\theta\\
&=&1-\frac{(\,\vec{a}\cdot \vec{b}\,)^2}{(\,|\vec{a}|\,|\vec{b}|\,)^2}\\
&=&\frac{(\,|\vec{a}|\,|\vec{b}|\,)^2-(\,\vec{a}\cdot \vec{b}\,)^2}{(\,|\vec{a}|\,|\vec{b}|\,)^2}
\end{eqnarray}\)
\(\,\theta\,\)は三角形の内角になるので\(\,\sin\theta\,＞\,0\,\)として良く
\(\begin{eqnarray}\displaystyle
\sin\theta&=&\sqrt{\frac{(\,|\vec{a}|\,|\vec{b}|\,)^2-(\,\vec{a}\cdot \vec{b}\,)^2}{(\,|\vec{a}|\,|\vec{b}|\,)^2}}\\ \\
&=&\frac{\sqrt{(\,|\vec{a}|\,|\vec{b}|\,)^2-(\,\vec{a}\cdot \vec{b}\,)^2}}{|\vec{a}|\,|\vec{b}|}
\end{eqnarray}\)
ここで面積の公式に代入すると
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{S}}&=&\frac{1}{2}\,|\vec{a}|\,|\vec{b}|\,\sin \theta\\
&=&\frac{1}{2}\,|\vec{a}|\,|\vec{b}|\,\frac{\sqrt{(\,|\vec{a}|\,|\vec{b}|\,)^2-(\,\vec{a}\cdot \vec{b}\,)^2}}{|\vec{a}|\,|\vec{b}|}\\
&=&\color{red}{\frac{1}{2}\,\sqrt{(\,|\vec{a}|\,|\vec{b}|\,)^2-(\,\vec{a}\cdot \vec{b}\,)^2}}
\end{eqnarray}\)
覚える価値あるのか？と思えてしまう形ですよね。笑
覚えておく価値あります！
もう少しスマートに証明しておきます。
\(\begin{eqnarray}\displaystyle
\mathrm{S}&=&\frac{1}{2}\,|\vec{a}|\,|\vec{b}|\,\sin \theta\\
\Leftrightarrow 2\mathrm{S}&=&|\vec{a}|\,|\vec{b}|\,\sin \theta
\end{eqnarray}\)
両辺\(\,2\,\)乗して
\(\begin{eqnarray}
4\mathrm{S^2}&=&|\vec{a}|^2\,|\vec{b}|^2\,\sin^2 \theta\\
&=&|\vec{a}|^2\,|\vec{b}|^2\,(\,1-\cos^2\theta\,)\\
&=&|\vec{a}|^2\,|\vec{b}|^2-|\vec{a}|^2\,|\vec{b}|^2\,\cos^2\theta\\
&=&|\vec{a}|^2\,|\vec{b}|^2-(\color{red}{|\vec{a}|\,|\vec{b}|\,\cos\theta})^2\\
&=&|\vec{a}|^2\,|\vec{b}|^2-(\,\color{red}{\vec{a}\cdot\vec{b}}\,)^2\\ \\
\mathrm{S}^2&=&\frac{|\vec{a}|^2\,|\vec{b}|^2-(\,\vec{a}\cdot\vec{b}\,)^2}{4}
\end{eqnarray}\)
\(\,\mathrm{S\,＞\,0}\,\)だから
\(\displaystyle \color{red}{\mathrm{S}=\frac{\sqrt{|\vec{a}|^2\,|\vec{b}|^2-(\,\vec{a}\cdot\vec{b}\,)^2}}{2}}\)
平行四辺形の場合は三角形2つ分なので
平行四辺形の面積を\(\,\mathrm{S’}\,\)とすると
\(\begin{eqnarray}
\color{red}{\mathrm{S’}=\sqrt{|\vec{a}|^2\,|\vec{b}|^2-(\,\vec{a}\cdot\vec{b}\,)^2}}
\end{eqnarray}\)
となります。
面積を求める例題
教科書にある公式を利用する場合と例題で比較してみましょう。
四角形\(\,\mathrm{ABCD}\,\)は，辺\(\,\mathrm{AD}\,\)と辺\(\,\mathrm{BC}\,\)が平行で，\(\,\mathrm{AB＝DC}\,\)，\(\,\mathrm{∠ABC=∠BCD}\,\)を満たすとする。
さらに，
\(\,\mathrm{\overrightarrow{OA}}=\vec{a}\,\)，\(\,\mathrm{\overrightarrow{OB}}=\vec{b}\,\)，\(\,\mathrm{\overrightarrow{OA}}=\vec{c}\,\)として
\(\,|\,\vec{a}\,|=1\,\)，\(\,|\,\vec{b}\,|=\sqrt{3}\,\)，\(\,|\,\vec{c}\,|=\sqrt{5}\,\)
\(\,\vec{a}\,\cdot\,\vec{b}=1\,\)，\(\,\vec{b}\,\cdot\,\vec{c}=3\,\)，\(\,\vec{a}\,\cdot\,\vec{c}=0\,\)
であるとする。
三角形\(\,\mathrm{OAC}\,\)の面積を求めよ。
見たことあるでしょう？
\(\,2019\,\)年度のセンター試験数学\(\,\mathrm{ⅡB}\,\)の第\(\,4\,\)問の冒頭です。
問題は四角錐ですが関係ありません。
センター試験では(1)があって\(\,\mathrm{∠AOC}\,\)を求める誘導がついています。
内積の定義から
\(\hspace{10pt}\vec{a}\,\cdot\,\vec{c}=|\,\vec{a}\,||\,\vec{c}\,|\,\cos \mathrm{∠AOC}\)
なので
\(\begin{eqnarray}\displaystyle
\cos \mathrm{∠AOC}&=&\frac{\vec{a}\,\cdot\,\vec{c}}{|\,\vec{a}\,||\,\vec{c}\,|}\\
&=&\frac{0}{1\cdot \sqrt{5}}\\
&=&0
\end{eqnarray}\)
\(\displaystyle ∴ \theta=\frac{\pi}{2}\)
※
センタ試験では\(\color{black}{\fbox{\(\,90^{\circ}\,\)}}\)と答えます。
とすると
\(\begin{eqnarray}\displaystyle
△\mathrm{OAC}&=&\frac{1}{2}\,|\,\vec{a}\,|\,|\,\vec{c}\,|\,\sin \frac{\pi}{2}\\
&=&\frac{1}{2}\times 1\times \sqrt{5}\times 1\\
&=&\underline{ \frac{\sqrt{5}}{2} }
\end{eqnarray}\)
共通テストなどでは誘導に乗るこの方法の方が良いです。
というよりこのような計算だけで求めていくのは最後までつながりません。
では、先ほどの公式を使って三角形の面積を出しておきましょう。
\(\begin{eqnarray}\displaystyle
△\mathrm{AOC}&=&\frac{1}{2}\sqrt{|\,\vec{a}\,|^2\,|\,\vec{c}\,|^2-(\vec{a}\,\cdot\,\vec{c})^2}\\
&=&\frac{1}{2}\sqrt{1\cdot 5-(0)^2}\\
&=&\underline{ \frac{\sqrt{5}}{2} }
\end{eqnarray}\)
わかりますか、この違い。
共通テストなどは基本の確認問題が続くので誘導されますが、私立入試や\(\,2\,\)次（本）試験などでは角度を求める部分は飛びます。
もちろん、角度を求めておくことが基本で後に応用が効きます。
しかし、私立だと小問集合で面積を聞かれることも少なくありませんので時間を稼ぐ意味では覚えておくと良い公式です。
もう少し例題を出しておきたいですが長くなったので自分で探してみてください。
三角比の面積を求める問題でも使えますけど、難関校を受験予定がない場合は覚えなくても良いです。笑
共通テストではいつも通り誘導に乗りましょう。
基本を大切にしておけば共通テストなどでは十分です。