平面ベクトルの要点をまとめておきます。
演算や成分、内積など基本用語の定義から位置ベクトルと図形表示まで簡単にまとめておきますので確認しておきましょう。
ベクトルは平面と空間を分けて考える必要はないのですが、教科書的な分類をしています。
ここでは短時間で復習できるように定義、定理の確認だけにしましたが、長いです。
直感的に理解できる人は、リンク先の練習問題で使い方を確認してください。
※
まとめてみて、基本例題を解いていない（解説していない）ことに気がつきました。笑
（笑い事ではありませんね。ごめんなさい。）
教科書の例題や練習問題レベルの問題解説もこのページに追加していきますのでたまに帰ってきてください。笑笑
（他分野の例題等もそれぞれの「要点ページ」に追加していく予定にしています。）
平面ベクトルの演算
平面ベクトルと空間ベクトルを分けてまとめますが、
ベクトルを理解したければ空間までの基本的な確認が済んだ後にもう一度全体を見渡して下さい。
新しい表示方法になるので定義定理は多いです。
ただし、ポイントがそれほど多くあるわけではありません。
ベクトルとは
ベクトルを定義するために有効線分という言葉を説明しておきます。
\(\color{red}{\fbox{ 有効線分 }}\)
線分に向きを付けて考えたものを有効線分という。
線分\(\,\mathrm{AB}\,\)は長さを持っていますが方向性はありません。
この線分の\(\,\mathrm{A}\,\)を始点、\(\,\mathrm{B}\,\)を終点とすると方向が定まります。
この方向を持った線分を有効線分といい、\(\,\overrightarrow{\mathrm{AB}}\,\)と表します。
また、有効線分は、始点、向き、長さを決めると定まります。
この3つの要素のうち、向きと長さだけに注目し、
始点の違いを無視することでベクトルが定義できます。
\(\color{red}{\fbox{ 有効線分とベクトル }}\)
与えられた有効線分は1つのベクトルを定める。
1つの有効線分と向きも長さも等しい有効線分は、
ベクトルとしては、同じものを定めるものとする。
こう言うとわかりにくいのですが、大切なポイントなのです。
どういうことかというと、
向きと長さが同じ有効線分はたくさんありますが、
ベクトルで表すと1つ、だということです。
例えば、平行四辺形\(\,\mathrm{ABCD}\,\)の\(\,\mathrm{AB}\,\)と\(\,\mathrm{DC}\,\)は平行で長さも同じなので、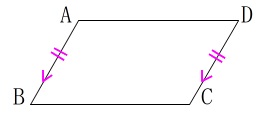
有効線分の\(\,\mathrm{\overrightarrow{AB}}\,\)と\(\,\mathrm{\overrightarrow{DC}}\,\)は、
始点を同じにして重ねると同じものなので、
1つの（同じ）ベクトルを表します。
\(\hspace{10pt}\mathrm{\overrightarrow{AB}}=\mathrm{\overrightarrow{DC}}\)
同じように平行四辺形\(\,\mathrm{ABCD}\,\)において
\(\hspace{10pt}\mathrm{\overrightarrow{AD}}=\mathrm{\overrightarrow{BC}}\)
ベクトルの表し方は始点を先に終点を後に書き、上に右向きの矢印を付けます。
普通は、1つの文字の上に矢印を付けて
\(\hspace{10pt}\overrightarrow{\mathrm{OA}}=\vec{a}\,,\,\overrightarrow{\mathrm{OB}}=b\)
などと表します。
こうすると
\(\hspace{10pt}\mathrm{\overrightarrow{AB}}=\mathrm{\overrightarrow{DC}}=\vec{a}\)
と向きと長さが同じ有効線分が一つで表されることが分かり易くなります。
ここまでをまとめて『ベクトルの相等』といいますがややこしくなるので省略します。笑
どこが大切なポイントかまだ分からないかもしれませんが、
『始点を一つに』
というベクトル問題を扱うときの重要な手順につながるのです。
\(\color{red}{\fbox{ 逆ベクトル }}\)
ベクトル\(\,\vec{a}\,\)の向きを逆にしたベクトルを
\(\,\vec{a}\,\)の逆ベクトルといい \(\,\overrightarrow{-a}\,\) で表す。
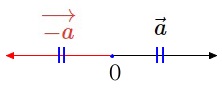つまり、
\(\hspace{10pt}\mathrm{\overrightarrow{AB}}=\vec{a}\,\)
とするとき
\(\hspace{10pt}\mathrm{\overrightarrow{BA}}=\overrightarrow{-a}\,\)
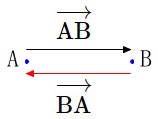すなわち
\(\hspace{10pt}\color{red}{\mathrm{\overrightarrow{BA}}=-\overrightarrow{\mathrm{AB}}}\)
です。
ここで\(\,\vec{0}\,\)についてもまとめておきたいところですが演算の中で説明します。
ベクトルの演算
ベクトルが何か分ければ、
足し算や引き算や実数倍する計算は普通にやっても良いので簡単にまとめます。
ただ、面白い性質もありますが注意点もあるので必ず確認しておいてください。
ベクトルの和
\(\color{red}{\fbox{ ベクトルの和の定義 }}\)
3点\(\,\mathrm{A,B,C}\,\)に対し
\(\hspace{10pt}\color{red}{\vec{a}=\overrightarrow{\mathrm{AB}}}\)
\(\hspace{10pt}\color{red}{\vec{b}=\overrightarrow{\mathrm{BC}}}\)
とするとき、
\(\hspace{10pt}\color{red}{\vec{a}+\vec{b}=\overrightarrow{\mathrm{AC}}}\)
と定義する。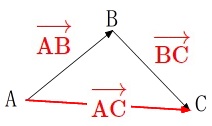
これは\(\,\vec{a}\,\)の終点と\(\,\vec{b}\,\)の始点を一致させるという条件を満たせば、
二つのベクトルの和は
\(\,\vec{a}\,\)の始点から\(\,\vec{b}\,\)の終点へのベクトルになる。
ということです。
\(\hspace{10pt}\overrightarrow{\mathrm{\color{red}{A}\color{blue}{B}}}+\overrightarrow{\mathrm{\color{blue}{B}\color{magenta}{C}}}=\overrightarrow{\mathrm{\color{red}{A}\color{magenta}{C}}}\)
この\(\,\overrightarrow{\mathrm{AC}}\,\)に\(\,\mathrm{C}\,\)を始点とするベクトルを加えても成り立つので、
\(\hspace{10pt}\mathrm{\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CP}=\overrightarrow{AP}}\)
といくつでも加えていくことができます。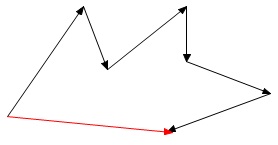
\(\color{red}{\fbox{ ベクトルの加法の性質 }}\)
\(\hspace{10pt}\vec{a}+\vec{b}=\vec{b}+\vec{a} 交換法則\)
\(\hspace{10pt}(\,\vec{a}+\vec{b}\,)+\vec{c}=\vec{a}+(\,\vec{b}+\vec{c}\,) 結合法則\)
加法（足し算）においてはベクトルでも交換法則と結合法則は成り立ちます。
ゼロベクトル
\(\color{red}{\fbox{ ゼロ（零）ベクトルの定義 }}\)
始点と終点が一致した有効線分\(\,\mathrm{\overrightarrow{AA}}\,\)によって代表されるベクトルを、
ゼロベクトルといい、\(\,\vec{0}\,\)と表す。
\(\,\vec{0}\,\)の大きさは\(\,0\,\)であり、向きは考えない。
ゼロベクトルについて次の性質が成り立ちます。
\(\color{red}{\fbox{ 零ベクトルの性質 }}\)
\(\hspace{10pt}\color{red}{\vec{a}+(-\vec{a})=\vec{0}}\)
\(\hspace{10pt}\color{red}{\vec{a}+\vec{0}=\vec{a}}\)
ベクトルの減法
\(\color{red}{\fbox{ ベクトルの減法 }}\)
\(\hspace{10pt}\color{red}{\vec{a}-\vec{b}=\vec{a}+(-\vec{b})} (定義)\)
\(\hspace{10pt}\color{red}{\vec{a}-\vec{a}=\vec{0}}\)
説明は不要でしょう。
ここで一つ重要な事実を強調しておきます。
\(\hspace{10pt}\vec{b}+\vec{c}=\vec{a}\)
のとき
\(\hspace{10pt}\vec{c}=\vec{a}-\vec{b}\)
となり、\(\,\vec{c}\,\)は\(\,\vec{a}\,\)と\(\,\vec{b}\,\)の差になっています。
これはベクトル\(\,\vec{c}\,\)が\(\,\vec{b}\,\)と\(\,\vec{a}\,\)の終点を結んだベクトルを意味します。
そこで、一般的に成り立つベクトルの始点を変える方法を示しておきます。
これは必ず覚えておきましょう。
\(\hspace{10pt}\color{red}{\mathrm{\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}}}\)
始点は何に変えても同じです。
新しい始点から元の終点へのベクトルから
新しい始点から元の始点へのベクトルを引く
と同じベクトルを表します。
この操作をすればすべてのベクトルは始点を一つで表すことができます。
これは簡単なことですがベクトルを扱う上で非常に大切になりますよ。
位置ベクトルの説明でもう一度確認します。
次は実数倍ですが細かい説明は無しにして計算法則を示しておきます。
\(\color{red}{\fbox{ ベクトルの実数倍の性質 }}\)
\(\,\vec{a}\,,\,\vec{b}\,\)を任意のベクトル、\(\,x\,,\,y\,\)を任意の実数とする。
\(\hspace{10pt}\color{red}{x(\,\vec{a}+\vec{b}\,)=x\,\vec{a}+x\,\vec{b}}\)
\(\hspace{10pt}\color{red}{(\,x+y\,)\vec{a}=x\,\vec{a}+y\,\vec{a}}\)
\(\hspace{10pt}\color{red}{x\,(\,y\,\vec{a}\,)=(\,x\,y\,)\vec{a}}\)
\(\hspace{10pt}\color{red}{1\,\vec{a}=\vec{a}}\)
\(\hspace{10pt}\color{red}{(-1)\vec{a}=-\vec{a}}\)
\(\hspace{10pt}\color{blue}{0\,\vec{a}=\vec{0}}\)
\(\hspace{10pt}\color{red}{\vec{a}+\vec{0}=\vec{a}}\)
\(\hspace{10pt}\color{blue}{x\,\vec{0}=\vec{0}}\)
文字式同様、普通に計算して良いということですが、
\(\hspace{10pt}\color{blue}{\vec{0}}\,\)となる等式において、
ゼロベクトルは\(\,0\,\)ではないので間違えないようにしましょう。
ベクトルの平行条件
\(\color{red}{\fbox{ ベクトルの平行条件 }}\)
\(\,\vec{a}≠\vec{0}\,,\,\vec{b}≠\vec{0}\,\)のとき
\(\hspace{10pt}\vec{a}\) ∥ \(\vec{b}\)
\(\hspace{10pt} ⇔ \vec{b}=k\,\vec{a}\) となる実数\(\,k\,\)が存在する。
これは始点を同じにすれば\(3\)点が一直線上にある条件と同じになるので後で図形との関係で説明します。
単位ベクトル
\(\color{red}{\fbox{ 単位ベクトルの定義 }}\)
大きさが\(\,1\,\)のベクトルを単位ベクトルという。
また、一般的に次のことがいえます。
\(\,\vec{a}≠\vec{0}\,\)のとき、\(\,\vec{a}\,\)と平行な単位ベクトルは
\(\hspace{10pt}\displaystyle \frac{\vec{a}}{|\vec{a}|} および -\frac{\vec{a}}{|\vec{a}|}\)
である。
これは忘れている人多くないですか？
ベクトルの分解
ここは非常に大切で簡単にまとめられる部分ではないのですが、
教科書程度のまとめとしておきます。
一般に、\(\,\vec{a}\,,\,\vec{b}\,\)がともに\(\,\vec{0}\,\)ではなく平行でもないとき、
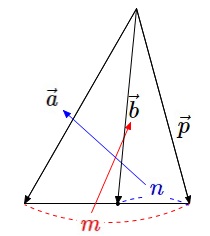
任意のベクトル\(\,\vec{p}\,\)は、適当な実数\(\,s\,,\,t\,\)を用いて、
ただ一通りにだけ、
\(\hspace{10pt}\color{red}{\vec{p}=s\,\vec{a}+t\,\vec{b}}\)
と必ず表すことができる。
平面上において\(\,\vec{a}\,,\,\vec{b}\,\)がともに\(\,\vec{0}\,\)ではなく平行でもない二つのベクトルを、
\(\hspace{10pt}\vec{a}\,,\,\vec{b}\)は\(\,1\,\)次独立または線型独立であるといいます。
また、\(\,1\,\)次独立な2つのベクトルを用いて表すとき
ただ一通りにだけ、
にしかならない性質を一意性といいますが、別のところで説明します。
⇒ ベクトルと図形 線型独立（一次独立）と係数の一意性の利用法
これは図形への応用になるので後回しでも良いです。
すでに長くなっているのでもっと手短にまとめましょう。笑
平面ベクトルの成分
平面ベクトルの成分は\(\,x\,\)成分と,\(\,y\,\)成分に分けられます。
（空間では\(\,z\,\)成分も出てきますがここは平面ベクトルなので二つです。）
座標を利用します。
関数とかで使う\(\,x-y\,\)の直交座標なので慣れてしまえば簡単です。
\(\hspace{10pt}\color{blue}{\vec{e_1}=(\,1\,,\,0\,)} , \color{blue}{\vec{e_2}=(\,0\,,\,1\,)}\)
を基本ベクトルといい、これを標準基底といいます。
それぞれは軸の正の向きをもつ単位ベクトルです。
座標を考えるとこの二つの標準基底で座標上のすべての座標が表せます。
例えば、\(\,\mathrm{A\,(\,3\,,\,-2\,)}\,\)という座標は、
原点から、
\(\,x\,\)軸方向に\(\,3\,\)
\(\,y\,\)軸方向に\(\,-2\,\)
移動すれば定まります。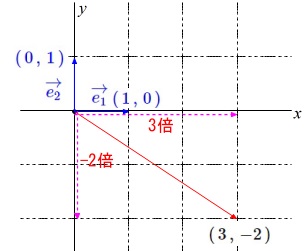
つまり、
\(\hspace{10pt}\vec{e_1}=(\,1\,,\,0\,)\)を\(\,3\,\)倍、
\(\hspace{10pt}\vec{e_2}=(\,0\,,\,1\,)\)を\(\,-2\,\)倍
したものを加えると点\(\,\mathrm{A(\,3\,,\,-2\,)}\,\)になります。
これをベクトルで表すと、
\(\hspace{10pt}\overrightarrow{\mathrm{OA}}=3\vec{e_1}+(-2)\vec{e_2}\)
となります。
これを基本ベクトル表示といいます。
一般的に表すと
平面ベクトル\(\,\vec{a}\,\)は基本ベクトルを用いて
\(\hspace{10pt}\color{red}{\vec{a}=a_1\vec{e_1}+a_2\vec{e_2}}\)
と表示され、\(\,\vec{a}\,\)の基本ベクトル表示という。
このとき、係数\(\,a_1\,,\,a_2\,\)を\(\,x\,\)成分、\(\,y\,\)成分という。
このことは今までの座標と同じ感覚でいいです。
\(\color{red}{\fbox{ ベクトルの成分表示 }}\)
平面ベクトル\(\,\vec{a}\,\)の\(\,x\,\)成分、\(\,y\,\)成分が
それぞれ\(\,a_1\,,\,a_2\,\)であるとき、
\(\hspace{10pt}\color{red}{\vec{a}=a_1\vec{e_1}+a_2\vec{e_2}}\)
これを簡単に
\(\hspace{10pt}\color{red}{\vec{a}=(\,a_1\,,\,a_2\,)}\)
で表す。これを\(\,\vec{a}\,\)の成分表示という。
単なる座標とベクトルの違いは、
\(\hspace{10pt}(\,a_1\,,\,a_2\,)\)
を点の座標とみているか、原点を始点としているベクトルとみているかの違いだと考えて良いです。
座標上のどの二点間のベクトルも、
原点を始点のベクトルに換えることができるということですね。
成分表示されたベクトルの大きさ
大きさは別のところでもまとめていますが、
成分表示されたベクトルの大きさは二点間の距離と同じです。
\(\color{red}{\fbox{ 成分表示のベクトルの大きさ }}\)
\(\vec{a}=(\,a_1\,,\,a_2\,)\)の大きさ\(\,|\,\vec{a}|\,\)は
\(\hspace{10pt} \color{red}{|\,\vec{a}|=\sqrt{a_1^2+a_2^2}}\)
で与えられる。
同じように\(\,2\,\)点で定まるベクトルの大きさも求まります。
\(\,2\,\)点\(\,\mathrm{A}(\,a_1\,,\,a_2\,),\mathrm{B}(\,b_1\,,\,b_2\,)\,\)において、
\(\hspace{10pt}\color{blue}{\overrightarrow{\mathrm{AB}}=(\,b_1-a_1\,,\,b_2-a_2\,)}\)
\(\hspace{10pt}\color{blue}{|\overrightarrow{\mathrm{AB}}|=\sqrt{(b_1-a_1)^2+(b_2-a_1)^2\,}}\)
これは内積と一緒に後で詳しく説明しますが、覚えておきましょう。
中学数学で学んだ座標上の二点間の距離と同じです。
平面ベクトルの内積
内積の意味は考えなくて良いです。笑
\(\color{red}{\fbox{ 内積の定義と記号 }}\)
\(\vec{a}\,,\,\vec{b}\,\)がともに\(\,\vec{0}\,\)でないとき、
実数\(\hspace{10pt}\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos \theta\)
を\(\,\vec{a}\,\)、\(\,\vec{b}\,\)の内積\(\,\vec{a}\cdot \vec{b}\,\)という。
このとき\(\,\theta\,\)は\(\,\vec{a}\,\)と\(\,\vec{b}\,\)のなす角である。
また、\(\vec{a}\,,\,\vec{b}\,\)のいずれかが\(\,\vec{0}\,\)のときの内積は\(\,0\,\)と定める。
\(\hspace{10pt}\,\vec{a}\cdot \vec{0}=\vec{0}\cdot \vec{b}=0\,\)
内積の結果は実数なので\(\,\vec{0}\,\)（ゼロベクトル）ではないことに注意してください。
内積の「\(\,\cdot\,\)」（点、ドット）は「\(\,\times \)」（掛け算の記号）としないように！
内容は簡単です。ただし、注意点には目を通しておいてください。
\(\color{red}{\fbox{ 内積の対称性 }}\)
\(\hspace{10pt}\color{red}{\vec{a}\cdot \vec{b}=\vec{b}\cdot\vec{a}}\)
これは定義から明らかですね。
さらに、内積の定義から\(\,\theta\,\)によって符号が変わるので次のことがいえます。
\(\color{red}{\fbox{ ベクトルのなす角と内積 }}\)
\(\,\theta\,\)が鋭角 ⇔ \(\,\vec{a}\cdot \vec{b}\,＞\,0\,\)
\(\,\theta\,\)が直角 ⇔ \(\,\vec{a}\cdot \vec{b}\,=\,0\,\)
\(\,\theta\,\)が鈍角 ⇔ \(\,\vec{a}\cdot \vec{b}\,＜\,0\,\)
さらに、\(\,\vec{a}=\vec{b}\,\)の場合を考えると公式が出てきます。
\(\color{red}{\fbox{ ベクトルの大きさと内積の関係 }}\)
\(\hspace{10pt}\,\color{red}{\vec{a}\cdot \vec{a}\,=\,|\vec{a}|^2}\,\) , \(\color{red}{\sqrt{\vec{a}\cdot \vec{a}\,}=|\vec{a}|}\)
「大きさを見たら\(2\)乗する」、というお決まりの作業をするときに何気なく使っているでしょう？
なす角\(\,\theta=0\,\)なのですぐに分かることですが、それでいいですよ。
成分表示による内積の定理
\(\color{red}{\fbox{ 内積の成分表示 }}\)
２つの平面ベクトル\(\,\vec{a}\,\)、\(\,\vec{b}\,\)の成分表示が
\(\vec{a}=(\,a_1\,,\,a_2\,)\)、\(\,\vec{b}=(\,b_1\,,\,b_2\,)\,\)ならば
\(\hspace{10pt}\color{red}{\vec{a}\cdot \vec{b}=a_1b_1+a_2b_2}\)
内積は定義とこの定理を同時に覚えておきましょう。
定義と定理を組合わせるとなす角\(\,\theta\,\)を求める式が出てきます。
\(\color{red}{\fbox{ ベクトルのなす角の余弦 }}\)
\(\vec{0}\,\)でない2つのベクトル\(\,\vec{a}=(\,a_1\,,\,a_2\,)\)、\(\,\vec{b}=(\,b_1\,,\,b_2\,)\,\)のなす角\(\,\theta\,\)は
\(\begin{eqnarray}\displaystyle
\hspace{10pt} \color{red}{\cos\theta}&\color{red}{=}&\color{red}{\frac{\vec{a}\cdot \vec{b}}{|\vec{a}|\,|\vec{b}|}}\\
&\color{red}{=}&\color{red}{\frac{a_1b_1+a_2+b_2}{\sqrt{a_1^2+a_2^2\,\sqrt{b_1^2+b_2^2\,}}}}
\end{eqnarray}\)
また内積の成分表示を利用して垂直条件と平行条件が関係式で出ます。
\(\color{red}{\fbox{ ベクトルの垂直条件 }}\)
\(\vec{0}\,\)でない2つのベクトル\(\,\vec{a}=(\,a_1\,,\,a_2\,)\)、\(\,\vec{b}=(\,b_1\,,\,b_2\,)\,\)が垂直になるとき、
\(\hspace{10pt}\color{red}{a_1b_1+a_2b_2\,=0}\)
2つのベクトル\(\,\vec{a}=(\,\color{red}{a_1}\,,\,\color{red}{a_2}\,)\)、\(\,\vec{b}=(\,\color{blue}{b_1}\,,\,\color{blue}{b_2}\,)\,\)が平行であるときは
\(\vec{b}=k\vec{a}=(\,\color{blue}{k\,a_1}\,,\,\color{blue}{k\,a_2}\,)\)なので
\(\hspace{10pt}\color{red}{a_1}\times \color{blue}{k\,a_2}-\color{red}{a_2}\times \color{blue}{k\,a_1}=0\)
となることから次のことがいえます。
\(\color{red}{\fbox{ ベクトルの平行条件 }}\)
\(\vec{0}\,\)でない2つのベクトル\(\,\vec{a}=(\,a_1\,,\,a_2\,)\)、\(\,\vec{b}=(\,b_1\,,\,b_2\,)\,\)が平行になるとき、
\(\hspace{10pt}\color{red}{a_1b_2-a_2b_1\,=0}\)
これは分からないなら無視して良いです。笑
また、内積について次の性質も成り立ちます。
\(\color{red}{\fbox{ 内積の性質 }}\)
\(\hspace{10pt}\color{red}{(\,\vec{a}+\vec{b}\,)\cdot \vec{c}=\vec{a}\cdot \vec{c}+\vec{b}\cdot \vec{c}}\)
\(\hspace{10pt}\color{red}{\vec{a}\cdot (\,\vec{b}+\vec{c}\,)=\vec{a}\cdot \vec{b}+\vec{a}\cdot \vec{c}}\)
\(\hspace{10pt}\color{red}{(\,k\,\vec{a}\,)\,\vec{b}=\vec{a}\cdot (\,k\,\vec{b}\,)=k\,(\,\vec{a}\cdot \vec{b}\,)}\)（\(\,k\,\)は実数）
普通に展開しているのと同じです。
ここまで覚えていれば計算は大丈夫です。
内積の基本問題といえるでしょう。
問題を解くときの基本作業を書いておきました。
面積も求められるようになっています。
面積は図形との関係を見ながら進めた方が分かり易いので後回しでも良いですが、
全体を見渡せたら確認しておいてください。
試験時間を稼ぎたいなら覚えておくといい公式です。
やっとベクトルの便利さが分かるところまで来ました。笑
ベクトルと平面図形
数学\(\,\mathrm{ⅠA}\,\)では座標や図形は別物として学んできましたが、
ベクトルを使えば両方をまとめて利用できます。
位置ベクトル
例えば、平面上に\(\,3\,\)点\(\,\mathrm{A,B,C}\,\)があったとします。
このとき\(\,\overrightarrow{\mathrm{AB}}\,\)と\(\,\overrightarrow{\mathrm{AC}}\,\)で\(\,\mathrm{△ABC}\,\)は表されますが、
\(\,\overrightarrow{\mathrm{AB}}\,\)と\(\,\overrightarrow{\mathrm{AC}}\,\)はどこにあるかは定まっていません。
（平行移動してもベクトルは同じだからです。）
そこで、基準点として原点\(\,\mathrm{O}\,\)を定めると、
\(\,\overrightarrow{\mathrm{OA}}\,\)は1つのベクトルになるので\(\,\mathrm{△ABC}\,\)も1つに定まります。
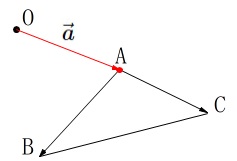つまり、\(\,\mathrm{△ABC}\,\)の位置は、
\(\,\mathrm{O}\,\)に対する\(\,\mathrm{A}\,\)の位置を\(\,\overrightarrow{\mathrm{OA}}=\vec{a}\,\)と定めれば一通りに表せる、ということです。
このように、基準点に対するベクトルを「位置ベクトル」といいます。
基準点はどこでも良いのですが、多くの場合原点にすると都合が良いです。
ある点に対し、基準点から対応させるベクトルが位置ベクトルだと分かれば必要ないですが定義としてまとめておきます。
\(\color{red}{\fbox{ 位置ベクトルの定義 }}\)
平面に定点\(\,\mathrm{O}\,\)を固定する。
この平面上の任意の点\(\,\mathrm{P}\,\)に対し、
有効線分\(\,\overrightarrow{\mathrm{OP}}\,\)が定めるベクトル\(\,\vec{p}\,\)を対応させることができる。
このベクトル\(\,\vec{p}\,\)を、
\(\hspace{10pt}\mathrm{O}\,\)を基準点とする\(\,\mathrm{P}\,\)の位置ベクトル
という。
また、点\(\,\mathrm{P}\,\)の位置ベクトルが\(\,\vec{p}\,\)であることを
\(\hspace{10pt}\mathrm{P}(\,\vec{p}\,)\,\)
と表し、位置ベクトル\(\,\vec{p}\,\)で表された点は\(\,\mathrm{P}\,\)であることを意味する。
定義を見るとややこしいので、
基準点（原点）を定めればすべての図形をベクトルを用いて固定して考えることができる、と考えておけば良いです。
ベクトルの減法で書きましたが、
2点\(\,\mathrm{A}(\,\vec{a}\,)\,,\,\mathrm{B}(\,\vec{b}\,)\,\)に対し、
\(\hspace{10pt}\,\overrightarrow{\mathrm{AB}}=\vec{b}-\vec{a}\,\)
となります。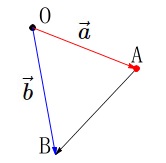
基準点を\(\,\mathrm{O}\,\)とすると
\(\hspace{10pt}\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}\)
⇔ \(\hspace{10pt}\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\)
こうして何度も見てくると「当たり前の事実」に思えてきたでしょう？
また、直線の方程式を求めるとき、傾きとその直線が通る\(1\)点があれば求まります。
傾きが同じ直線はたくさんあるけど、ある\(1\)点を通る直線は\(1\)本しかない、
直線が固定できる、というのと同じです。
基準点を定めることで位置ベクトルを利用して固定できる、ということです。
ベクトル方程式を見た後ならさらに納得できると思うので全体を見てからもう一度見ておいてください。
内分点と外分点の位置ベクトル
内分点と外分点の位置関係は図形と方程式や平面図形で確認しておきましょう。
位置ベクトルを利用すると同様の計算ができます。
\(\color{red}{\fbox{ 内分点の位置ベクトル }}\)
異なる\(\,2\,\)点\(\,\mathrm{A}(\,\vec{a})\,\)、\(\,\mathrm{B}(\,\vec{b})\,\)を、
\(\,m:n\,\)に内分する点\(\,\mathrm{P}\,\)の位置ベクトル\(\,\vec{p}\,\)は
\(\hspace{10pt}\displaystyle \vec{p}=\frac{n\,\vec{a}+m\,\vec{b}}{m+n}\)
特に、\(\,\mathrm{AB}\,\)の中点\(\,\mathrm{M}\,\)の位置ベクトル\(\,\vec{t}\,\)は
\(\hspace{10pt}\displaystyle \vec{t}=\frac{\vec{a}+\vec{b}}{2}\)
外分点は形式的に\(\,m:(-n)\,\)に内分とすれば良いです。
\(\color{red}{\fbox{ 外分点の位置ベクトル }}\)
異なる\(\,2\,\)点\(\,\mathrm{A}(\,\vec{a})\,\)、\(\,\mathrm{B}(\,\vec{b})\,\)を、
\(\,m:n\,\)に外分する点\(\,\mathrm{P}\,\)の位置ベクトル\(\,\vec{p}\,\)は
\(\hspace{10pt}\displaystyle \vec{p}=\frac{-n\,\vec{a}+m\,\vec{b}}{m-n}\)
内分点、外分点の証明はベクトルを使えば簡単です。
（こんなことをやっているから長くなるんですよね。笑）
点\(\,\mathrm{P}\,\)が線分\(\,\mathrm{AB}\,\)を\(\,\color{red}{m}:\color{blue}{n}\,\)に内分しているということは、
位置から考えて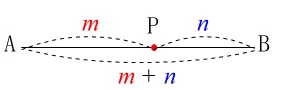
\(\hspace{10pt}\displaystyle \overrightarrow{\mathrm{AB}}=\frac{\color{red}{m}+\color{blue}{n}}{\color{red}{m}}\,\overrightarrow{\mathrm{AP}}\)
となっています。
これはこれで始点を\(\,\mathrm{A}\,\)とすれば\(\,\mathrm{P}\,\)は\(\,\mathrm{AB}\,\)を\(\,m:n\,\)に内分していることを意味しています。
しかし、始点を\(\,\mathrm{O}\,\)とすると、
\(\begin{eqnarray}\displaystyle
\overrightarrow{\mathrm{AB}}&=&\frac{m+n}{m}\,\overrightarrow{\mathrm{AP}}\\
\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}&=&\frac{m+n}{m}\,(\,\overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OA}}\,)\\
\vec{b}-\vec{a}&=&\frac{m+n}{m}(\vec{p}-\vec{a})
\end{eqnarray}\)
これを変形すれば
\(\hspace{10pt}\displaystyle \vec{p}=\frac{n}{m+n}\,\vec{a}+\frac{m}{m+n}\,\vec{b}\)
となります。
（外分点の場合も同様にやってみてください。）
三角形の重心の位置ベクトル
\(\color{red}{\fbox{ 重心の位置ベクトル }}\)
\(\,\mathrm{△ABC}\,\)において、\(\,\mathrm{A}(\vec{a})\,\)、\(\,\mathrm{B}(\vec{b})\,\)、\(\,\mathrm{C}(\vec{c})\,\)ならば
重心の位置ベクトル\(\,\vec{g}\,\)は
\(\hspace{10pt}\displaystyle \vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}\)
少なくとも、「重心って何？」という状態は抜け出しておきましょう。笑
⇒ 三角形の五心（重心・外心・内心・垂心・傍心）と定理の証明
三角形の五心は問題の一部になり易いです。
というか、問題から外す方が難しい。
ベクトルの図形への応用
ここからは別に解説してあるのでリンク先で確認してください。
\(\color{red}{\fbox{ 異なる３点が一直線上にある条件 }}\)
３点\(\,\mathrm{A,B,C}\,\)が異なるとき、
一直線上にある条件は
\(\hspace{10pt}\overrightarrow{\mathrm{AC}}=k\,\overrightarrow{\mathrm{AB}}\)
となる実数kが存在することである。
始点を1つにして考えれば平行条件とほぼ同じです。
⇒ 平面ベクトルの内分点外分点の利用と3点が一直線上にある証明
内分点、外分点とともに再確認しておきましょう。
⇒ ベクトルと図形 線型独立（一次独立）と係数の一意性の利用法
ここで再度確認しておきましょう。
もちろん、幾何の定理は使って構いませんよ。
むしろ使えないと共通テストでも厳しいでしょう。
説明が雑になってない？と思ったあなた。
鋭い！
でも、長くなりすぎて、めんどくさっ、、、と思っているわけではないですよ。笑
この程度の復習にそれほど時間をかけなくても良いだろう、という効率化を考えているのです。
ベクトルによる図形表示
図形といっても直線や円がほとんどなので難しくはありません。
\(\,xy\,\)座標系で表していたものをベクトルを利用して表現するだけです。
ベクトル方程式
\(\color{red}{\fbox{ ベクトル方程式とは }}\)
点\(\,\mathrm{P}(\,\vec{p}\,\))が曲線\(\,\mathrm{C}\,\)上にある条件を、
\(\hspace{10pt}\vec{p}\)を用いて表した方程式
を\(\,\mathrm{C}\,\)のベクトル方程式という。
抽象的すぎて意味が分からないので、具体的に方程式を示しましょう。
\(\color{red}{\fbox{ 円のベクトル方程式 }}\)
点\(\,\mathrm{C}(\vec{c})\,\)を中心する半径\(\,r\,\)の円周を表すベクトル方程式は、
\(\hspace{10pt}|\,\vec{p}-\vec{c}\,|=r\)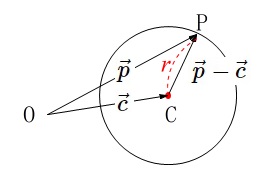
円の定義に添ってベクトルを利用して表しただけです。
\(\,xy\,\)座標で中心\(\,\mathrm{C}(\,a\,,\,b\,)\,\)、半径\(\,r\,\)とすると
\(\hspace{10pt}(x-a)^2+(y-b)^2=r^2\)
と同じことです。
\(\color{red}{\fbox{ ２点を通る直線のベクトル方程式 }}\)
異なる２点\(\,\mathrm{A}(\,\vec{a}\,)\,\)、\(\,\mathrm{B}(\,\vec{b}\,)\,\)を直線のベクトル方程式は
\(\hspace{10pt}\vec{p}=(1-t)\vec{a}+t\vec{b}\)
このとき\(\,1-t=s\,\)とすると
\(\hspace{10pt}\vec{p}=s\vec{a}+t\vec{b} (\,s+t=1\,)\)
とも表せる。
\(\,\overrightarrow{\mathrm{AP}}\,\)に平行な直線はいくつもありますが、
基準点\(\,\mathrm{O}\,\)から\(\,\mathrm{A}\,\)にベクトルを固定することで直線\(\,\mathrm{AP}\,\)に乗ります。
その後\(\,\overrightarrow{\mathrm{AB}}\,\)を\(\,t\,\)倍すれば\(\,\vec{p}\,\)になるので
\(\begin{eqnarray}
\vec{p}&=&\overrightarrow{\mathrm{OA}}+t\,\overrightarrow{\mathrm{AB}}\\
&=&\vec{a}+t\,(\,\vec{b}-\vec{a}\,)\\
&=&(1-t)\,\vec{a}+t\,\vec{b}
\end{eqnarray}\)
と簡単に示せます。
（直線に乗るには\(\,\mathrm{A}\,\)でなくて直線上のどの点でも良いです。）
これは2つのベクトル\(\,\mathrm{A}(\,\vec{a}\,)\,\)、\(\,\mathrm{B}(\,\vec{b}\,)\,\)の、
終点を結ぶ直線上の点を、ベクトル\(\,\vec{a}\,,\,\vec{b}\,\)の線型結合で表したとき、
係数の和が\(\,1\,\)になるということの証しです。
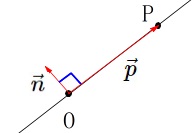
\(\color{red}{\fbox{ 原点を通る直線のベクトル方程式 }}\)
\(\,\vec{n}\,\)を\(\,\vec{0}\,\)でないベクトルとすると
原点を通り\(\,\vec{n}\,\)と直交するベクトル方程式は
\(\hspace{10pt}\vec{p}\cdot\vec{n}=0\)
これは内積が\(\,0\,\)になることから直感的に分かるでしょう。
平行移動して原点から離れた場合もベクトル方程式で表せます。
ただし、\(\,\vec{n}\,\)は直線の法線ベクトルとします。
\(\color{red}{\fbox{ ある点を通り法線ベクトルに垂直な直線のベクトル方程式 }}\)
\(\vec{n}\)≠\(\vec{0}\)を与えられたベクトル、
\(\,\mathrm{P_0}(\,\vec{p_0})\,\)を与えられた点とする。
\(\,\mathrm{P_0}\,\)を通り、\(\,\vec{n}\,\)と直交する直線のベクトル方程式は
\(\hspace{10pt}(\,\vec{p}-\vec{p_0}\,)\cdot \vec{n}=0\)
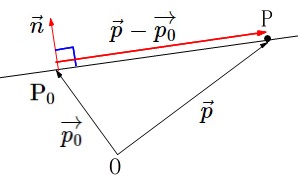一般化することもできますがベクトル方程式はここまでで十分です。
方向ベクトル\(\,\vec{p}-\vec{p_0}\,\)を用いて、
\(\hspace{10pt}\vec{p}=\vec{p_0}+t\,(\,\vec{p}-\vec{p_0}\,)\)
としても良いです。
ただ、法線ベクトルを利用することも多いので両方使えると良いですね。
後はベクトル方程式と成分を利用して\(\,xy\,\)座標系の方程式に置き換えることです。
直線の媒介変数と成分表示
直線のベクトル方程式
\(\begin{eqnarray}
\vec{p}&=&\overrightarrow{\mathrm{OA}}+\color{blue}{t}\,\overrightarrow{\mathrm{\color{red}{AB}}}\\
&=&\vec{a}+\color{blue}{t}\,(\,\color{red}{\vec{b}-\vec{a}}\,)
\end{eqnarray}\)
において、
\(\overrightarrow{\mathrm{\color{red}{AB}}}\) または \(\color{red}{\vec{b}-\vec{a}}\)
を方向ベクトルといい、\(\,t\,\)を媒介変数といいます。
媒介変数を用いて表すことを（そのまま）媒介変数表示といいます。
上の式はベクトル形の媒介変数表示です。
これに成分を加えます。
方向ベクトルが\(\,\vec{u}\,\)の直線\(\,\ell\,\)のベクトル方程式
\(\hspace{10pt}\ell : \vec{p}\,=\vec{a}+t\vec{u}\)
において
\(\vec{p}\,=(\,x\,,\,y\,)\,\)
\(\vec{a}\,=(\,x_0\,,\,y_0\,)\)
\(\vec{u}\,=(\,a\,,\,b\,)\)
とすると、
\(\begin{eqnarray}
(\,x\,,\,y\,)&=&(\,x_0\,,\,y_0\,)+t\,(\,a\,,\,b\,)\\
&=&(\,x_0+at\,,\,y_0+tb\,)
\end{eqnarray}\)
この成分を別々に書き出すと
\( \begin{cases}
\hspace{7pt} x=x_0+ta\\
\hspace{7pt} y=y_0+tb
\end{cases}\)
となります。
これを成分による媒介変数表示といいます。
（普通に媒介変数表示といっているのはこっちです。）
この媒介変数表示された\(\,t\,\)を消去すると\(\,xy\,\)座標での方程式が求まります。
\(\hspace{10pt}\ell : a\,(\,x-x_0\,)-b\,(\,y-y_0\,)=0\)
法線ベクトルの成分が分かる場合も媒介変数を消去して方程式が求まります。
点\(\,\mathrm{P_0}(x_0\,,\,y_0\,)\,\)を通り、\(\,\vec{n}=(\,a\,,\,b\,)\,\)に垂直な直線は
\(\hspace{10pt}a(x-x_0)+b(y-y_0)=0\)
\(\,\vec{n}\,\)が法線ベクトルですよ。
一般に、直線\(\,ax+by+c=0\,\)の法線ベクトルの1つは\(\,\vec{n}=(\,a\,,\,b\,)\,\)です。
円の媒介変数表示も説明に加えておきたいところですが長くなりすぎたようです。
平面ベクトルの要点はここまでにします。
よく見かける点のベクトル方程式の面積比問題です。
長くなりましたが以上です。
空間ベクトルを分けました。
しかし、ベクトルをすでに習っている人は平面と空間を分けずに見ておくことをおすすめします。
成分が1つ増えるだけなので、別分野と考えるよりは理解が深まります。
※
空間ベクトルには平面の方程式が発展として取り入れられています。
ここを掘り下げると直線の方程式から説明することになる（したくなる？）ので、
その項目だけでも平面ベクトル程度では済まないくらい長くなります。
なので、手を出さないようにします。笑
⇒ 共通テスト(センター試験)数学の勉強法と対策まとめ単元別攻略と解説
共通テストの対策としては応用問題を時間をかけて解いていくよりも、
各分野の基本的なことを一つひとつ抑えていく方が得点は上がります。