2019年(平成31年度)に行われたセンター試験数学2Ｂ第4問の解説です。
第4問は空間ベクトルの問題で面積および体積を求めすが問題の順番通りに進めていけばそれほど難しい問題ではありません。
空間では図形がイメージしにくいので図に頼り切ることはできませんが、大まかな配置は確認しておいた方が良いです。
正答はセンターが発表していますので確認してください。
この問題は数学ⅡBの部分のみの問題です。
第\(\,4\,\)問は選択問題のベクトルです。
『センター試験の数学解説』平成としては最後の問題になりますね。
終わってしまったものはさっさとかたづけてしまいましょう。笑
ただ、共通テストになってもベクトルの問題を解く方針は変わりませんよ。
条件を整理しておきましょう。
(1)の前にある条件は最後まで使う条件です。
底面\(\,\mathrm{ＡＢＣＤ}\,\)の四角錐\(\,\mathrm{ＯＡＢＣＤ}\,\)
\(\,\mathrm{\color{red}{AD /\!/ BC}}\,\)
\(\,\mathrm{\color{red}{ＡＢ=ＣＤ}}\,\)
\(\,\mathrm{\color{red}{∠ABC=∠BCD}}\,\)
さらに
\(\,\overrightarrow{\mathrm{OA}}=\vec{a}\,,\,\,\overrightarrow{\mathrm{OB}}=\vec{b}\,,\,\,\overrightarrow{\mathrm{OC}}=\vec{c}\)
として
\(\,\color{red}{|\,\vec{a}\,|=1}\,,\,\,\color{red}{|\,\vec{b}\,|=\sqrt{3}}\,,\,\,\color{red}{|\,\vec{c}\,|=\sqrt{5}}\)
\(\,\color{red}{\vec{a}\,\cdot\,\vec{b}=1}\,,\,\,\color{red}{\vec{b}\,\cdot\,\vec{c}=3}\,,\,\,\color{red}{\vec{a}\,\cdot\,\vec{c}=0}\)
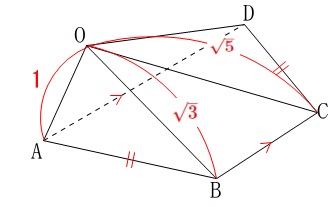
だいたいの位置関係です。
(1)
\(\,\vec{a}\,\cdot\,\vec{c}=0\,\)
より \(\,\mathrm{OA}\,\) ⊥ \(\,\mathrm{OC}\,\)
\(\,\mathrm{∠AOC=\color{black}{\fbox{\(\color{red}{ 90 }\)}}^{\circ}}\,\)
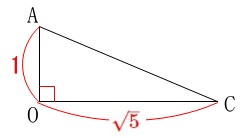なので
\(\begin{eqnarray}
\mathrm{△OAC}&=&\frac{1}{2}\times 1\times \sqrt{5}\\
&=&\frac{\sqrt{\color{black}{\fbox{\(\color{red}{ 5 }\)}}}}{\color{black}{\fbox{\(\color{red}{ 2 }\)}}}
\end{eqnarray}\)
(2)
ベクトルでは基本的な設定や方法は決まっています。
その最初が始点を1つにする、ということです。
問題で基底ベクトルを3つ用意してくれていますがすべて始点は\(\,\mathrm{O}\,\)なので\(\,\mathrm{O}\,\)で統一します。
\(\begin{eqnarray}
\overrightarrow{\mathrm{BA}}&=&\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\\
&=&\vec{a}-\vec{b}
\end{eqnarray}\)
\(\begin{eqnarray}
\overrightarrow{\mathrm{BC}}&=&\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}\\
&=&\vec{c}-\vec{b}
\end{eqnarray}\)
これから
\(\begin{eqnarray}
\overrightarrow{\mathrm{BA}}\cdot\overrightarrow{\mathrm{BC}}&=&(\vec{a}-\vec{b})(\vec{c}-\vec{b})\\
&=&\vec{a}\cdot\vec{c}-\vec{a}\cdot\vec{b}-\vec{b}\cdot\vec{c}+\vec{b}\cdot\vec{b}\\
&=&0-1-3+(\sqrt{3})^2\\
&=&\color{black}{\fbox{\(\color{red}{ -1 }\)}}
\end{eqnarray}\)
また、
ベクトルの大きさを見たら\(\,2\,\)乗する
これもお決まりにしておくといいです。
\(\begin{eqnarray}
|\,\overrightarrow{\mathrm{BA}}\,|^2&=&|\,\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\,|^2\\
&=&(\vec{a}-\vec{b})^2\\
&=&|\,\vec{a}\,|^2-2\,\vec{a}\cdot \vec{b}+|\,\vec{b}\,|^2\\
&=&1^2-2\times 1+(\sqrt{3})^2\\
&=&2\\
|\,\overrightarrow{\mathrm{BA}}\,|&=&\sqrt{\color{black}{\fbox{\(\color{red}{ 2 }\)}}}
\end{eqnarray}\)
同様に
\(\begin{eqnarray}
|\,\overrightarrow{\mathrm{BC}}\,|^2&=&|\,\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}\,|^2\\
&=&(\vec{a}-\vec{b})^2\\
&=&|\,\vec{c}\,|^2-2\,\vec{c}\cdot \vec{b}+|\,\vec{b}\,|^2\\
&=&(\sqrt{5})^2-2\times 3+(\sqrt{3})^2\\
&=&2\\
|\,\overrightarrow{\mathrm{BC}}\,|&=&\sqrt{\color{black}{\fbox{\(\color{red}{ 2 }\)}}}
\end{eqnarray}\)
内積の定義
\(\begin{eqnarray}\displaystyle
\overrightarrow{\mathrm{BA}}\cdot\overrightarrow{\mathrm{BC}}&=&|\,\overrightarrow{\mathrm{BA}}\,|\cdot |\,\overrightarrow{\mathrm{BC}}\,|\,\cos∠\mathrm{ABC}
\end{eqnarray}\)
から
\(\begin{eqnarray}\displaystyle
\cos∠\mathrm{ABC}&=&\frac{\,\overrightarrow{\mathrm{BA}}\cdot\overrightarrow{\mathrm{BC}}\,}{|\,\overrightarrow{\mathrm{BA}}\,|\cdot |\,\overrightarrow{\mathrm{BC}}\,|}\\
&=&\frac{-1}{\sqrt{2}\cdot \sqrt{2}}\\
&=&-\frac{1}{2}
\end{eqnarray}\)
よって
\(\,\mathrm{∠ABC=\color{black}{\fbox{\(\color{red}{ 120 }\)}}^{\circ}}\,\)
底面について条件がありました。
\(\,\mathrm{\color{red}{AD /\!/ BC}}\,\)
\(\,\mathrm{\color{red}{ＡＢ=ＣＤ}}\,\)
\(\,\mathrm{\color{red}{∠ABC=∠BCD}}\,\)
これに
\(\,\mathrm{∠ABC}=120^{\circ}\,\)
が加わると、
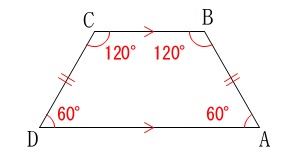
\(\,\mathrm{ ∠BAC=∠ADC=\color{black}{\fbox{\(\color{red}{ 60 }\)}}^{\circ}}\,\)
先に出している長さ
\(\overrightarrow{\mathrm{BA}}=\overrightarrow{\mathrm{BC}}=\sqrt{2}\)
と合わせて見ると実際に計算するまでもありませんが、
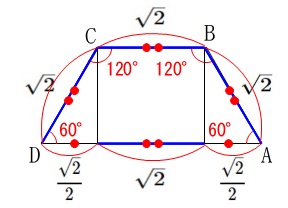
\(\overrightarrow{\mathrm{AD}}=\color{black}{\fbox{\(\color{red}{ 2 }\)}}\,\overrightarrow{\mathrm{BC}}\)
であり、空間では基底ベクトル3つで表すのが基本なので、
\(\begin{eqnarray}
\overrightarrow{\mathrm{OD}}&=&\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AD}}\\
&=&\overrightarrow{\mathrm{OA}}+2\,\overrightarrow{\mathrm{BC}}\\
&=&\vec{a}+2(\vec{c}-\vec{b})\\
&=&\vec{a}-\color{black}{\fbox{\(\color{red}{ 2 }\)}}\vec{b}+\color{black}{\fbox{\(\color{red}{ 2 }\)}}\vec{c}
\end{eqnarray}\)
等脚台形\(\,\mathrm{ＡＢＣＤ}\,\)の面積は、って高校入試か？
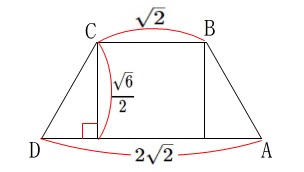
\(\begin{eqnarray}
(台形ＡＢＣＤ)&=&\frac{1}{2}\times (\sqrt{2}+2\sqrt{2})\times \frac{\sqrt{6}}{2}\\
&=&\frac{1}{2}\times 3\sqrt{2}\times \frac{\sqrt{6}}{2}\\
&=&\frac{3\sqrt{12}}{4}\\
&=&\frac{6\sqrt{3}}{4}\\
&=&\frac{\color{black}{\fbox{\(\color{red}{ 3 }\)}}\sqrt{\color{black}{\fbox{\(\color{red}{ 3 }\)}}}}{\color{black}{\fbox{\(\color{red}{ 2 }\)}}}
\end{eqnarray}\)
実際の試験では、図はしっかり書くけど、高校生なら計算はもう少し飛ばせるはずです。
(3)
『三角錐\(\,\mathrm{BOAC}\,\)の体積\(\,V\,\)を求めよう。』
です。
『求めよ。』でもおかしくはない問題ですが誘導してくれると言っているのです。
誘導に乗るんですよ。
条件を書き出しておきます。
\(\color{red}{\fbox{ 追加条件 }}\)
\(\,3\,\)点\(\,\mathrm{O,A,C}\,\)を通る平面を\(\,\alpha\,\)とする。
点\(\,\mathrm{H}\,\)は\(\,\alpha\,\)上の点で
\(\,\overrightarrow{\mathrm{BH}} ⊥ \vec{a}\,\)
\(\,\overrightarrow{\mathrm{BH}} ⊥ \vec{c}\,\)
実数\(\,t,s\,\)を用いて
\(\,\overrightarrow{\mathrm{BH}}=a\,\vec{a}+t\,\vec{c}\,\)と表す。
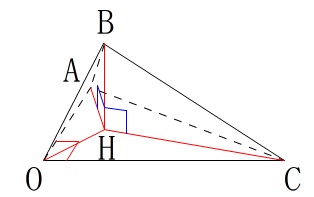面\(\,\mathrm{OAC}\,\)と\(\,\mathrm{BH}\,\)が垂直なので、
面\(\,\mathrm{AOC}\,\)上の\(\,2\,\)点を結んでできるベクトルはすべて\(\,\mathrm{BH}\,\)に垂直です。
このことからすぐに
\(\color{blue}{\overrightarrow{\mathrm{BH}}\,\cdot \,\vec{a}}=\color{black}{\fbox{\(\color{red}{ 0 }\)}}\)
\(\color{magenta}{\overrightarrow{\mathrm{BH}}\,\cdot \,\vec{c}}=\color{black}{\fbox{\(\color{black}{ 0 }\)}}\)
始点を\(\,\mathrm{O}\,\)に変えることによって
\(\begin{eqnarray}
\overrightarrow{\mathrm{BH}}&=&\color{red}{\overrightarrow{\mathrm{OH}}}-\overrightarrow{\mathrm{OB}}\\
&=&\color{red}{s\,\vec{a}+t\,\vec{c}}-\vec{b}
\end{eqnarray}\)
なので
\(\begin{eqnarray}
\color{blue}{\overrightarrow{\mathrm{BH}}\,\cdot \,\vec{a}}&=&0\\
(s\,\vec{a}+t\,\vec{c}-\vec{b})\,\cdot \,\vec{a}&=&0\\
s\,|\vec{a}|^2+t\,\vec{c}\cdot\vec{a}-\vec{b}\cdot \vec{a}&=&0\\
s+0-1&=&0\\
s&=&\color{black}{\fbox{\(\color{red}{ 1 }\)}}
\end{eqnarray}\)
条件
\(\,\color{red}{|\,\vec{a}\,|=1}\,,\,\,\color{red}{|\,\vec{b}\,|=\sqrt{3}}\,,\,\,\color{red}{|\,\vec{c}\,|=\sqrt{5}}\)
\(\,\color{red}{\vec{a}\,\cdot\,\vec{b}=1}\,,\,\,\color{red}{\vec{b}\,\cdot\,\vec{c}=3}\,,\,\,\color{red}{\vec{a}\,\cdot\,\vec{c}=0}\)
はまだ使いますよ。
\(\begin{eqnarray}\displaystyle
\color{magenta}{\overrightarrow{\mathrm{BH}}\cdot \vec{c}}&=&0\\
(s\,\vec{a}+t\,\vec{c}-\vec{b})\cdot \vec{c}&=&0\\
s\,\vec{a}\cdot\vec{c}+t|\,\vec{c}\,|^2-\vec{b}\cdot\vec{c}&=&0\\
0+t(\sqrt{5})^2-3&=&0\\
5t&=&3\\
t&=&\frac{\color{black}{\fbox{\(\color{red}{ 3 }\)}}}{\color{black}{\fbox{\(\color{red}{ 5 }\)}}}
\end{eqnarray}\)
この\(\,s,t\,\)を\(\overrightarrow{\mathrm{BH}}\)に戻します。
\(\begin{eqnarray}
\overrightarrow{\mathrm{BH}}&=&\overrightarrow{\mathrm{OH}}-\overrightarrow{\mathrm{OB}}\\
&=&s\,\vec{a}+t\,\vec{c}-\vec{b}\\
&=&\vec{a}+\frac{3}{5}\,\vec{c}-\vec{b}
\end{eqnarray}\)
ベクトルの大きさを求めたかったら、\(\,2\,\)乗です。
\(\begin{eqnarray}
|\,\overrightarrow{\mathrm{BH}}\,|^2&=&\left(\,\vec{a}+\frac{3}{5}\,\vec{c}-\vec{b}\,\right)^2\\
&=&|\,\vec{a}\,|^2+\frac{9}{25}|\,\vec{c}\,|^2+|\,\vec{b}\,|^2+\frac{6}{5}\,\vec{a}\cdot\vec{c}-\frac{6}{5}\vec{b}\cdot \vec{c}-2\vec{a}\cdot\vec{b}\\
&=&1+\frac{9}{25}\times 5+3+0-\frac{6}{5}\times 3-2\\
&=&1+\frac{9}{5}+3-\frac{18}{5}-2\\
&=&2-\frac{9}{5}\\
&=&\frac{10-9}{5}\\
&=&\frac{1}{5}\\
|\,\overrightarrow{\mathrm{BH}}\,|&=&\sqrt{\frac{1}{5}}\\
&=&\frac{\sqrt{\color{black}{\fbox{\(\color{red}{ 5 }\)}}}}{\color{black}{\fbox{\(\color{red}{ 5 }\)}}}
\end{eqnarray}\)
これで三角錐の高さが出ました。
底面積は(1)で\(\,\mathrm{△OAC}\,\)を求めてあります。
\(\begin{eqnarray}
V&=&\frac{1}{3}\times\,\mathrm{△OAC} \,\times \,\mathrm{BH}\\
&=&\frac{1}{3}\times \frac{\sqrt{5}}{2}\times \frac{\sqrt{5}}{5}\\
&=&\frac{\color{black}{\fbox{\(\color{red}{ 1 }\)}}}{\color{black}{\fbox{\(\color{red}{ 6 }\)}}}
\end{eqnarray}\)
(4)錐体\(\,\mathrm{BOAC}\,\)の体積を\(\,V\,\)とすると
四角錐\(\,\mathrm{OABCD}\,\)の体積は、高さが共通なので
底面積の比 \(\,\mathrm{△ABC：△ABCD=1:3}\,\)
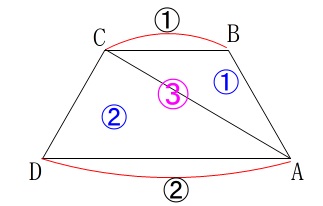となるので
\(\,(四角錐\mathrm{\,OABCD\,}の体積)=\color{black}{\fbox{\(\color{red}{ 3 }\)}}V\,\)
(3)では頂点を\(\,\mathrm{B}\,\)として体積を求めましたが、
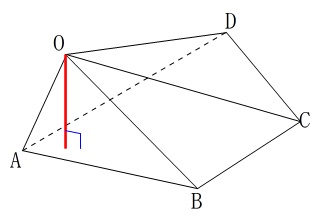頂点を\(\,\mathrm{O}\,\)としても体積は変わりません。
底面となる台形\(\,\mathrm{ABCD}\,\)の面積はすでに求めてあり。
\(\displaystyle \mathrm{(台形\,ABCD\,の面積)=\frac{3\sqrt{3}}{2}}\,\)
四角錐の高さを\(\,h\,\)とすると、体積は\(\,3V\,\)なので
\(\begin{eqnarray}
\frac{1}{3}\times \frac{3\sqrt{3}}{2}\times h&=&3\times \frac{1}{6}\\
\frac{\sqrt{3}}{2}h&=&\frac{1}{2}\\
h&=&\frac{1}{\sqrt{3}}\\
&=&\frac{\sqrt{\color{black}{\fbox{\(\color{red}{ 3 }\)}}}}{\color{black}{\fbox{\(\color{red}{ 3 }\)}}}
\end{eqnarray}\)
立体を転がすなんて高校入試のようだけど、
『総演習』通りやればベクトルとしても考えることがほとんどありませんね。
センター試験数学終了です。（と勘違いしていました。笑）
\(2020\)年度までセンター試験です。
共通テストになって何か変わるのかと言えば、
数学自体は変わらないんだから変わらないです。
第\(1\)問の三角関数と指数対数関数
⇒ センター試験数学2Ｂ2019年度第1問(三角関数と指数対数)の解説
第\(2\)問の基本的な微分積分
⇒ センター試験数学2Ｂ2019年度第2問(微分と積分)の解説
第\(3\)問の数列
⇒ センター試験数学2Ｂ2019年度選択問題第3問(数列)の解説
共通テストでどれだけ変えることができるのか、見物でもあります。
センター試験を廃止して共通テストとする意味はあるのでしょう。
たぶん。