2020年(令和2年)度に行われたセンター試験数学1Aの選択問題の1つ第5問平面幾何の解説です。
平面幾何（図形）で問われる定理はおおよそ限られているので基本的な定理をしっかり覚えていればそれほど得点しにくい分野ではありません。
今回はチェバ、メネラウス、方べきの定理が主な問題となります。
センター試験2020年度数学\(\,\mathrm{ⅠＡ}\,\)の問題です。
〔第５問〕平面幾何（図形）
利用する定理が基本的なものなので問題の意図は明らかです。
「図を描くこと。」
手を動かすという大切な基本を身に付けていれば、つまずくところは最後の定理の「逆」が利用できるかどうかだけです。
それも、相似を利用すれば中学生でも答えが出ます。
問題が簡単なので説明も簡単に済ませます。
（メンドクサイから手を抜くわけではありませんよ。笑）
チェバの定理、メネラウスの定理および面積比
条件を書き出しておきます。
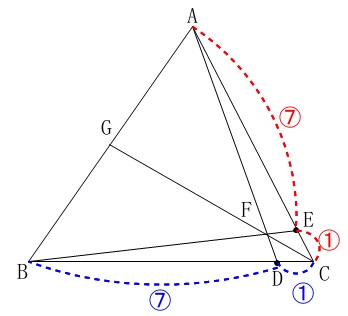
\(\,\mathrm{△ABC}\,\)において
\(\,\mathrm{BC}\,\)を\(\,7:1\,\)に内分する点を\(\,\mathrm{D}\,\)
\(\,\mathrm{AC}\,\)を\(\,7:1\,\)に内分する点を\(\,\mathrm{E}\,\)
\(\,\mathrm{AD}\,\)と\(\,\mathrm{BE}\,\)の交点を\(\,\mathrm{F}\,\)
\(\,\mathrm{CF}\,\)と\(\,\mathrm{AB}\,\)の交点を\(\,\mathrm{G}\,\)
とする。（線分、直線は問題で確認してください。）
言えることをすべて書き出しても良いのですが、
時間がかかるので問題に合わせて進めましょう。
先ずは\(\,\displaystyle \mathrm{\frac{GB}{AG}}\,\)の値です。
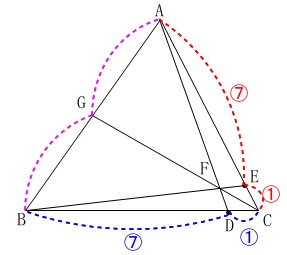ぐるっと\(\,1\,\)周できるのでチェバの定理ですね。
どこからはじめても良いですが、目的の線分比を先に持ってきましょう。
\(\begin{eqnarray}\displaystyle
\mathrm{\frac{AG}{GB}\cdot \frac{BD}{DC}\cdot \frac{CE}{EA}}&=&1\\
\mathrm{\frac{AG}{GB}\cdot \frac{7}{1}\cdot \frac{1}{7}}&=&1\\
\mathrm{\frac{AG}{GB}}&=&1
\end{eqnarray}\)
逆数をとっても同じです。
\(\displaystyle \mathrm{\frac{GB}{AG}}=\fbox{ 1 }\)
次に\(\,\displaystyle \mathrm{\frac{FD}{AF}}\,\)です。
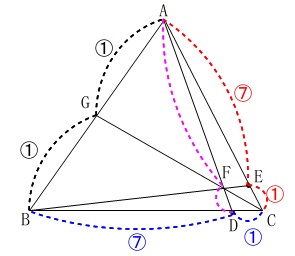メネラウスの定理ですね。
はじめるのはどこからでも良いですよ。
\(\begin{eqnarray}\displaystyle
\mathrm{\frac{AF}{FD}\cdot \frac{DB}{BC}\cdot \frac{CE}{EA}}&=&1\\
\mathrm{\frac{AF}{FD}\cdot \frac{7}{8}\cdot \frac{1}{7}}&=&1\\
\mathrm{\frac{AF}{FD}}&=&\frac{8}{1}\\
\end{eqnarray}\)
逆数をとって
\(\,\displaystyle \mathrm{\mathrm{\frac{FD}{AF}}=\frac{\fbox{ 1 }}{\fbox{ 8 }}}\,\)
同様に\(\displaystyle \,\mathrm{\frac{FC}{GF}}\,\)もメネラウスの定理を利用して、
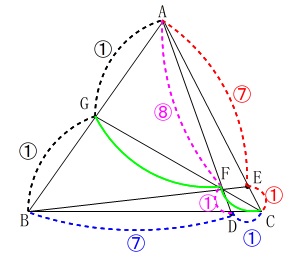\(\begin{eqnarray}\displaystyle
\mathrm{\frac{AB}{BG}\cdot \frac{GF}{FC}\cdot \frac{CE}{EA}}&=&1\\
\mathrm{\frac{2}{1}\cdot \frac{GF}{FC}\cdot \frac{1}{7}}&=&1\\
\mathrm{\frac{GF}{FC}}&=&\frac{7}{2}
\end{eqnarray}\)
逆数を取って
\(\hspace{10pt}\displaystyle \mathrm{\frac{FC}{GF}}=\frac{\fbox{ 2 }}{\fbox{ 7 }}\)
ここまでくると\(\,\mathrm{BF:FE}\,\)も出しておきたいですが必要無いので先に進みます。
次は\(\,\mathrm{△CDG}\,\)と\(\,\mathrm{△BFG}\,\)の面積比です。
\(\,\mathrm{△ABC}\,\)の面積を基準にしても良いですが、
\(\,\mathrm{△BCG}\,\)を基準にしても同じなので、
部分的に抜き出した（拡大した図の中で見やすい）\(\,\mathrm{△BCG}\,\)を基準にします。
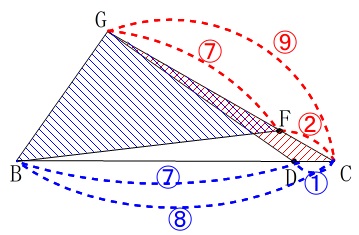基準とするだけなので面積を\(\,1\,\)としても良いです。
ここでは一般的に\(\,\mathrm{△BCG=S}\,\)とします。
高さが共通の三角形は、底辺の比が面積比になります。
\(\,\mathrm{\color{blue}{BC:DC=8:1}}\,\)なので
\(\begin{eqnarray}\displaystyle
\mathrm{△CDG}&=&\mathrm{△BCG}\times \frac{1}{8}\\
&=&\frac{1}{8}\mathrm{S}
\end{eqnarray}\)
\(\,\mathrm{\color{red}{CG:FG=9:7}}\,\)なので
\(\begin{eqnarray}\displaystyle
\mathrm{△BFG}&=&\mathrm{△BCG}\times \frac{7}{9}\\
&=&\frac{7}{9}\mathrm{S}
\end{eqnarray}\)
よって、
\(\begin{eqnarray}\displaystyle
\mathrm{\frac{△CDG}{△BFG}}&=&\frac{\frac{1}{8}\mathrm{S}}{\frac{7}{9}\mathrm{S}}\\
&=&\frac{1}{8}\times \frac{9}{7}\\
&=&\frac{\fbox{ 9 }}{\fbox{ 56 }}
\end{eqnarray}\)
円に内接する四角形と方べきの定理
条件が加わって続きます。
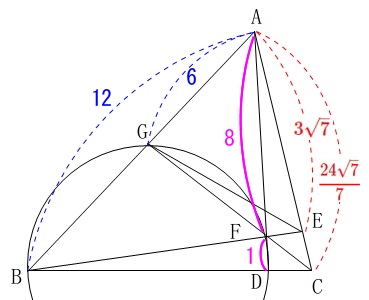
\(\,\mathrm{B,D,F,G}\,\)が同一円周上にある
\(\,\mathrm{FD=1}\,\)
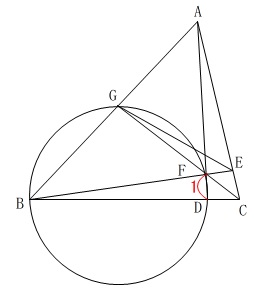長さの比を合わせると微妙な位置関係になっているので、
比率を無視して見やすくします。
相似な三角形を利用する方法
\(\,\mathrm{AF:FD=8:1}\,\)なので
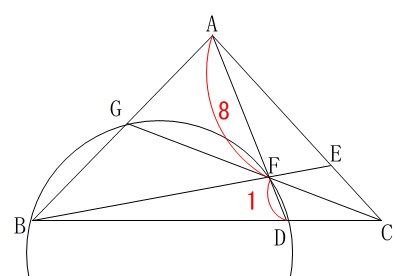このとき\(\,\mathrm{AB}\,\)の長さは相似な三角形の比から求まります。
定理を使うと、方べきの定理です。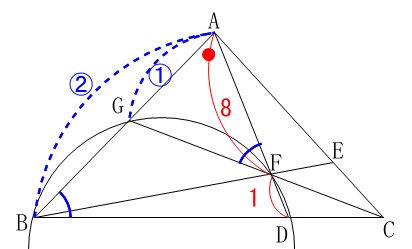
四角形\(\,\mathrm{BDFG}\,\)が円に内接しているので、
\(\,\mathrm{∠AFG=∠ABC}\,\)
\(\,\mathrm{∠BAD}\,\)は共通な角
なので\(\,2\,\)角相等から
\(\,\mathrm{△AFG}\,\) ∽ \(\,\mathrm{△ABD}\,\)
ここで\(\,\mathrm{AB}=x\,\)とすると\(\displaystyle \,\mathrm{AG}=\frac{1}{2}x\,\)なので、
\(\begin{eqnarray}
8:x&=&\frac{1}{2}x:9\\
\frac{1}{2}x^2&=&9\times 8\\
x^2&=&144
\end{eqnarray}\)
長さだから\(\,x\,＞\,0\,\)より
\(x=\mathrm{AB}=\fbox{ 12 }\)
方べきの定理で求める
方べきの定理が使えます。
\(\begin{eqnarray}
\mathrm{AF\cdot AD}&=&\mathrm{AG\cdot AB}\\
8\times 9&=&\frac{1}{2}x\cdot x\\
x^2&=&144
\end{eqnarray}\)
なので
\(\,\mathrm{AB}=x=\fbox{ 12 }\,\)
方べきの定理は相似から出てくる定理なので同じです。
時間に余裕がない人は方べきの定理でチャチャっと答えを出して良いですよ。
次に\(\,\mathrm{AE=\color{red}{3\sqrt{7}}}\,\)という条件が加わります。
\(\,\mathrm{AE:AC=7:8}\,\)なので
\(\begin{eqnarray}\displaystyle
\mathrm{AE:AC}&=&7:8\\
3\sqrt{7}:\mathrm{AC}&=&7:8\\
7\times \mathrm{AC}&=&8\times 3\sqrt{7}\\
\mathrm{AC}&=&\color{red}{\frac{24\sqrt{7}}{7}}
\end{eqnarray}\)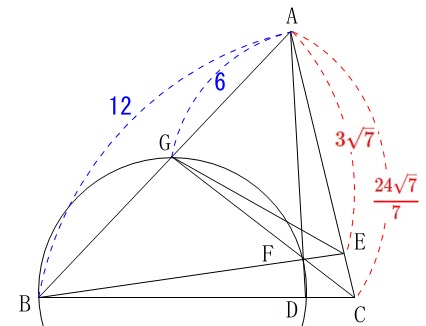
よって、
\(\begin{eqnarray}\displaystyle
\mathrm{AE\cdot AC}&=&\color{red}{3\sqrt{7}}\times \color{red}{\frac{24\sqrt{7}}{7}}\\
&=&\fbox{ \(\,\color{red}{72}\,\) }
\end{eqnarray}\)
この\(\,\color{red}{72}\,\)という数字が
\(\,\mathrm{AG\cdot AB}=\color{blue}{6}\times \color{blue}{12=}\color{blue}{72}\,\)
と同じであることに気がつけば、
方べきの定理
\(\,\mathrm{AE\cdot AC=AG\cdot AB}\,\)
が成り立っているので「方べきの定理の逆」から、
四角形\(\,\mathrm{BCEG}\,\)が円に内接している
ということが分かりますので先ほどと同じ理由で、
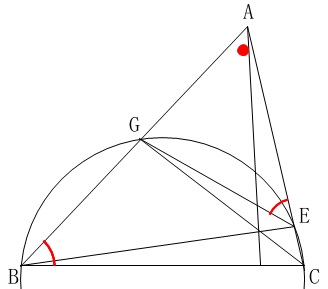
\(\,\mathrm{△AEG}\,\) ∽ \(\,\mathrm{△ABC}\,\)
であることが分かります。
よって、
\(\,\mathrm{∠AEG}=\fbox{ \(\,\mathrm{∠ABC}\,\) }\,\)
方べきの定理の逆が言えないとき、（気がつかないとき）
\(\mathrm{AE}=3\sqrt{7}≒8\)
なので、おおまかにですが長さの比を合わせると、
\(\,\mathrm{∠AEG}\,\)に近い角は、
\(\,\mathrm{∠ABC}\,\) か \(\,\mathrm{∠BAD}\,\)
と目論んで、
\(\,\mathrm{△AEG}\,\) ∽ \(\,\mathrm{△ABC}\,\) ではないか？
と探っても答えは出ますよ。笑
\(\begin{eqnarray}\displaystyle
\mathrm{\frac{AE}{AB}}&=&\frac{3\sqrt{7}}{12}\\
&=&\frac{\sqrt{7}}{4}
\end{eqnarray}\)
\(\begin{eqnarray}\displaystyle
\mathrm{\frac{AG}{AC}}&=&\frac{6}{\frac{24\sqrt{7}}{7}}\\
&=&6\times \frac{7}{24\sqrt{7}}\\
&=&\frac{\sqrt{7}}{4}
\end{eqnarray}\)
\(\,2\,\)組の辺の比が一致しました。
全体通じてそれほど時間はかからない問題なので、
結果が出ればどっちでも良いです。笑
\(\,2020\,\)年度、最後のセンター試験\(\,\mathrm{ⅠA}\,\)は以上です。
共通テストに名前は変わっても変わらないことは、
基本を抑えて、しっかり手を動かせば糸口さえ見つからないほどの難問は出題されないということです。