2020年(令和2年)度センター試験数学2Bの第4問の解説です。
第4問はベクトルで空間図形を扱いますが、平面上で考える問題が多いので少し見方を変えればそれほど苦戦もしなかったでしょう。
四角形の形状を聞かれますが、位置関係をつかめば中学校の図形問題です。
\(\,2020\,\)年度センター試験数学\(\,\mathrm{ⅡB}\,\)の問題です。
第４問空間座標とベクトル（四角形の形状と四角錐の体積）
平面ベクトルでも空間ベクトルでも大きさや内積の求め方は同じです。
設定された座標が無理数を含んでいますが、特別な問題ではありません。
前半はベクトルの定義と定理の確認問題です。
計算がややこしそうに見えますが、問題自体は簡単なのでさっさと済ませましょう。
ベクトルの大きさと内積
平面は同一直線上にない\(\,3\,\)点があれば定まります。
空間座標に\(\,2\,\)点\(\,\mathrm{A,B}\,\)があって
\(\,\mathrm{A\,(\,3\,,\,3\,,\,-6\,)}\,\)
\(\,\mathrm{B\,(\,2+\sqrt{3}\,,\,2-2\sqrt{3}\,,\,-4\,)}\,\)
これに原点\(\,\mathrm{O\,(\,0\,,\,0\,,\,0\,)}\,\)が加わり、平面\(\,\alpha\,\)が定まります。
求めると、平面\(\,\alpha\,\)の方程式は
\(\hspace{10pt}x+y-z=0\)
ですがなくても問題ありません。
あれば四面体の体積が誘導なしに求まりますが、使える人の方が少ないでしょう。
当会ではこの\(\,1\,\)年、空間座標における平面、直線の方程式を重点的に扱っていたので使いたくなりますが、
センター試験や共通テストのような問題には向きませんね。笑
問題の誘導通りに進めましょう。
(1)
ベクトルの大きさと内積です。
\(\,\mathrm{A\,(\,\color{red}{3}\,,\,\color{red}{3}\,,\,\color{red}{-6}\,)}\,\)
\(\,\mathrm{B\,(\,\color{blue}{2+\sqrt{3}}\,,\,\color{blue}{2-2\sqrt{3}}\,,\,\color{blue}{-4}\,)}\,\)
なので
\(\begin{eqnarray}
|\overrightarrow{\mathrm{OA}}|&=&\sqrt{\color{red}{3}^2+\color{red}{3}^2+(\color{red}{-6})^2}\\
&=&\sqrt{54}\\
&=&\fbox{ 3 }\sqrt{\fbox{ 6 }}
\end{eqnarray}\)
\(\begin{eqnarray}
\overrightarrow{\mathrm{OB}}|&=&\sqrt{(\color{blue}{2+2\sqrt{3}})^2+(\color{blue}{2-\sqrt{3}})^2+(\color{blue}{-4)}^2}\\
&=&\sqrt{(16+8\sqrt{3})+(16-8\sqrt{3})+16}\\
&=&\fbox{ 4 }\sqrt{\fbox{ 3 }}
\end{eqnarray}\)
\(\begin{eqnarray}
\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}&=&\color{red}{3}(\color{blue}{2+2\sqrt{3}})+\color{red}{3}(\color{blue}{2-2\sqrt{3}})+(\color{red}{-6})(\color{blue}{-4})\\
&=&6+6\sqrt{3}+6-6\sqrt{3}+24\\
&=&\fbox{ 36 }
\end{eqnarray}\)
これが分からない人は\(\,ⅡB\,\)の試験は受けていないと思いますが、
または
で確認しておいて下さい。
基底ベクトルと線型結合
平面\(\,\alpha\,\)上の点\(\,\mathrm{C}\,\)を\(\,s,t\,\)を用いて表します。
1つの平面上のベクトルはすべて、平面上の独立な2つのベクトル
（平行でもなく\(\,\mathrm{\overrightarrow{0}}\,\)でもない2つのベクトル）
を用いて表せますので、文字2つについて条件2つを考えれば良いだけですね。
基底にするベクトルは\(\,\mathrm{\overrightarrow{OA}}\,\)と\(\,\mathrm{\overrightarrow{OB}}\,\)です。
\(\begin{eqnarray}\displaystyle
\overrightarrow{\mathrm{OC}}&=&s\,\overrightarrow{\mathrm{OA}}+t\,\overrightarrow{\mathrm{OB}}\\
&=&s\,(\,3\,,\,3\,,\,-6\,)+t\,(\,2+2\sqrt{3}\,,\,2-2\sqrt{3}\,,\,-4\,)\\
&=&(\,3s+(2+2\sqrt{3})t\,,\,3s+(2-2\sqrt{3})t\,,\,-6s-4t\,)
\end{eqnarray}\)
見にくいので縦ベクトルに変えておきます。
\(\begin{eqnarray}
\overrightarrow{\mathrm{OC}}&=&s\,\overrightarrow{\mathrm{OA}}+t\,\overrightarrow{\mathrm{OB}}\\
&=&s\left(
\begin{array}{c}
3 \\
3 \\
-6 \\
\end{array}\right)
+t\left(
\begin{array}{c}
2+2\sqrt{3} \\
2-2\sqrt{3} \\
-4 \\
\end{array}\right)\\
&=&\left(
\begin{array}{c}
3\,s+(2+2\sqrt{3})\,t\\
3\,s+(2-2\sqrt{3})\,t\\
-6\,s-4\,t\\
\end{array}\right)
\end{eqnarray}\)
2つの条件は問題に書いてあります。
\(\,\mathrm{\overrightarrow{OA}}\,\)⊥\(\,\overrightarrow{\mathrm{OC}}\,\)
\(\,\mathrm{\overrightarrow{OB}}\cdot \overrightarrow{\mathrm{OC}}=24\,\)
①です。
\(\,\mathrm{\overrightarrow{OA}}\,\)⊥\(\,\overrightarrow{\mathrm{OC}}\,\)
から内積が\(\,0\,\)になるので（長くなるので途中の計算は自分でやって下さい。）
\(\begin{eqnarray}
\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OC}}&=&\left(
\begin{array}{c}
3 \\
3 \\
-6 \\
\end{array}\right)
\cdot
\left(
\begin{array}{c}
3\,s+(2+2\sqrt{3})\,t\\
3\,s+(2-2\sqrt{3})\,t\\
-6\,s-4\,t\\
\end{array}\right)\\
&=&54\,s+36\,t
\end{eqnarray}\)
これから
\(\,3\,s+2\,t=0 ･･･②\,\)
また\(\,\overrightarrow{\mathrm{OB}}\cdot \overrightarrow{\mathrm{OC}}\,\)は
\(\begin{eqnarray}
\overrightarrow{\mathrm{OB}}\cdot \overrightarrow{\mathrm{OC}}&=&\left(
\begin{array}{c}
2+2\sqrt{3} \\
2-2\sqrt{3} \\
-4 \\
\end{array}\right)
\cdot
\left(
\begin{array}{c}
3\,s+(2+2\sqrt{3})\,t\\
3\,s+(2-2\sqrt{3})\,t\\
-6\,s-4\,t\\
\end{array}\right)\\
&=&36\,s+48\,t
\end{eqnarray}\)
これが\(\,24\,\)になることから
\(\begin{eqnarray}
36\,s+48\,t&=&24\\
6\,s+8\,t&=&4 ･･･③
\end{eqnarray}\)
②③より
\(\hspace{10pt}\displaystyle s=\frac{\fbox{ －2 }}{\fbox{ 3 }}\,,\,t=\fbox{ 1 }\)
このとき
\(\begin{eqnarray}\displaystyle
\overrightarrow{\mathrm{OC}}&=&\left(
\begin{array}{c}
3\,s+(2+2\sqrt{3})\,t\\
3\,s+(2-2\sqrt{3})\,t\\
-6\,s-4\,t\\
\end{array}\right)\\
&=&\left(
\begin{array}{c}
3\,\left(\,\frac{-2}{3}\,\right)+(2+2\sqrt{3})\,(1)\\
3\,\left(\,\frac{-2}{3}\,\right)+(2-2\sqrt{3})\,(1)\\
-6\,\left(\,\frac{-2}{3}\,\right)-4\,(1)\\
\end{array}\right)\\
&=&\left(
\begin{array}{c}
-2+2+2\sqrt{3}\\
-2+2-2\sqrt{3}\\
4-4\\
\end{array}\right)\\
&=&\left(
\begin{array}{c}
2\sqrt{3}\\
-2\sqrt{3}\\
0\\
\end{array}\right)
\end{eqnarray}\)
よって
\(\begin{eqnarray}
|\overrightarrow{\mathrm{OC}}|&=&\sqrt{(2\sqrt{3})^2+(-2\sqrt{3})^2+0^2}\\
&=&\sqrt{24}\\
&=&\fbox{ 2 }\sqrt{\fbox{ 6 }}
\end{eqnarray}\)
ベクトルの大きさをとるとき通常なら\(\,2\,\)乗しますがその必要もないでしょう。
さて、
ここまで条件を処理しただけで何も考えていません。
四角形の形状
(3)
\(\begin{eqnarray}
\overrightarrow{\mathrm{CB}}&=&\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OC}}\\
&=&\left(
\begin{array}{c}
2+2\sqrt{3} \\
2-2\sqrt{3} \\
-4 \\
\end{array}\right)
–
\left(
\begin{array}{c}
2\sqrt{3}\\
-2\sqrt{3}\\
0\\
\end{array}\right)\\
&=&\left(
\begin{array}{c}
2\\
2\\
-4\\
\end{array}\right)
\end{eqnarray}\)
\(\hspace{10pt}\overrightarrow{\mathrm{CB}}=(\,\fbox{ 2 }\,,\,\fbox{ 2 }\,,\,\fbox{ －4 }\,)\)
これをぼーとながめている人に分からないだろうけど、
これって\(\,\overrightarrow{\mathrm{OA}}\,\)と同じ方向を向いていますので、
\(\,\overrightarrow{\mathrm{OA}}\,\)と\(\,\overrightarrow{\mathrm{CB}}\,\)は平行
です。
ただし、大きさは違うので台形です。
\(\begin{eqnarray}
|\overrightarrow{\mathrm{CB}}|&=&\sqrt{2^2+2^+(-4)^2}\\
&=&\sqrt{24}\\
&=&2\sqrt{6}
\end{eqnarray}\)
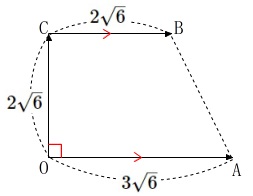答えは \(\,\underline{ ③ }\,\)
対辺の長さが違う時点で\(\,⓪①②\,\)は選択肢から外れますね。
また台形\(\,\mathrm{OABC}\,\)の面積\(\,S\,\)は、高さを\(\,\mathrm{|OC|}\,\)とする台形なので
\(\begin{eqnarray}\displaystyle
S&=&\frac{|\mathrm{CB}|+|\mathrm{OA}|}{2}\times |\mathrm{OC}|\\
&=&\frac{2\sqrt{6}+3\sqrt{6}}{2}\times 2\sqrt{6}\\
&=&5\sqrt{6}\times \sqrt{6}\\
&=&\fbox{ 30 }
\end{eqnarray}\)
空間座標と四面体の体積
ようやく平面\(\,\alpha\,\)から出ます。
条件は
\(\,\overrightarrow{\mathrm{OA}}\,\) ⊥ \(\,\overrightarrow{\mathrm{OD}}\,\)
\(\,\overrightarrow{\mathrm{OC}}\cdot \overrightarrow{\mathrm{OD}}=2\sqrt{6}\,\)
点\(\,\mathrm{D}\,\)の\(\,z\,\)座標が\(\,1\,\)
このときの\(\,\mathrm{D}\,\)の座標を
\((\,a\,,\,b\,,\,1\,)\)
とすると、
\(\,\overrightarrow{\mathrm{OA}}=(\,3\,,\,3\,,\,-6\,)\,\)
\(\,\overrightarrow{\mathrm{OC}}=(\,2\sqrt{3}\,,\,-2\sqrt{3}\,,\,0\,)\,\)
なので
\(\begin{eqnarray}
\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OD}}&=&\left(
\begin{array}{c}
3 \\
3 \\
-6 \\
\end{array}\right)
\cdot \left(
\begin{array}{c}
a \\
b \\
1 \\
\end{array}\right)\\
&=&3a+3b-6
\end{eqnarray}\)
垂直なので内積が\(\,0\,\)となることから
\(\begin{eqnarray}
3a+3b-6&=&0\\
a+b-2&=&0 ･･･\color{red}{(ⅰ)}
\end{eqnarray}\)
また
\(\begin{eqnarray}
\overrightarrow{\mathrm{OC}}\cdot \overrightarrow{\mathrm{OD}}&=&\left(
\begin{array}{c}
2\sqrt{3}\\
-2\sqrt{3}\\
0 \\
\end{array}\right)
\cdot \left(
\begin{array}{c}
a \\
b \\
1 \\
\end{array}\right)\\
&=&2\sqrt{3}\,a-2\sqrt{3}\,b
\end{eqnarray}\)
これが\(\,\color{blue}{2\sqrt{6}}\,\)であることから
\(\begin{eqnarray}
2\sqrt{3}\,a-2\sqrt{3}\,b&=&2\sqrt{6}\\
a-b&=&\sqrt{2} ･･･\color{blue}{(ⅱ)}
\end{eqnarray}\)
\(\,\color{red}{(ⅰ)}\,\)から
\(b=2-a\)
これを\(\,\color{blue}{(ⅱ)}\,\)に代入して、
\(\begin{eqnarray}
a-(2-a)&=&\sqrt{2}\\
2a-2&=&\sqrt{2}\\
2a&=&2+\sqrt{2}\\
a&=&\frac{2+\sqrt{2}}{2}\\
&=&1+\frac{\sqrt{2}}{2}
\end{eqnarray}\)
このとき
\(\begin{eqnarray}
b&=&2-a\\
&=&2-\left(1+\frac{\sqrt{2}}{2}\right)\\
&=&1-\frac{\sqrt{2}}{2}
\end{eqnarray}\)
よって点\(\,\mathrm{D}\,\)の座標は
\(\hspace{10pt}\displaystyle \left(\fbox{ 1 }+\frac{\sqrt{\fbox{ 2 }}}{\fbox{ 2 }},\fbox{ 1 }-\frac{\sqrt{\fbox{ 2 }}}{\fbox{ 2 }},1\right)\)
また
\(\begin{eqnarray}\displaystyle
|\overrightarrow{\mathrm{OD}}|&=&\sqrt{\left(1+\frac{\sqrt{2}}{2}\right)^2+\left(1-\frac{\sqrt{2}}{2}\right)^2+1^2}\\
&=&\sqrt{1+\sqrt{2}+\frac{1}{2}+1-\sqrt{2}+\frac{1}{2}+1}\\
&=&\sqrt{4}\\
&=&2
\end{eqnarray}\)
条件
\(\color{red}{\overrightarrow{\mathrm{OC}}}\cdot \color{blue}{\overrightarrow{\mathrm{OD}}}=2\sqrt{6}\)
より\(\,∠\mathrm{COD}=\theta\,\)とすると
\(\begin{eqnarray}\displaystyle
\color{red}{2\sqrt{6}}\cdot \color{blue}{2}\cdot \cos\theta &=&2\sqrt{6}\\
\cos \theta&=&\frac{1}{2}\\
\theta&=&\frac{2}{3}\pi
\end{eqnarray}\)
よって
\(\,∠\mathrm{COD}=\fbox{ 60 }^{\circ}\,\)
問題にも書いてありますが、
\(\,\mathrm{\overrightarrow{OA}}\,\) ⊥ \(\,\overrightarrow{\mathrm{OC}}\,\)
\(\,\overrightarrow{\mathrm{OA}}\,\) ⊥ \(\,\overrightarrow{\mathrm{OD}}\,\)
なので\(\,\mathrm{O,C,Dを}\,\)通る平面\(\,\beta\,\)は、\(\,\mathrm{\overrightarrow{OA}}\,\)に垂直です。
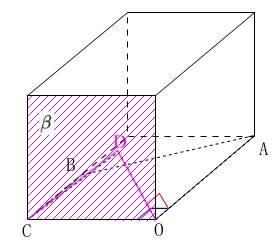四面体\(\,\mathrm{OABC}\,\)を底面と見たときの高さ\(\,h\,\)は、
点\(\,\mathrm{D}\,\)から平面\(\,\alpha\,\)への距離なので
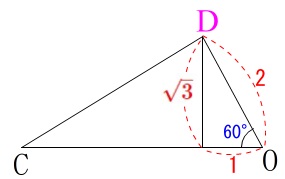\(\,∠\mathrm{COD}=\color{blue}{60^{\circ}}\,\)で\(\,|\overrightarrow{\mathrm{OD}}|=\color{red}{2}\,\)であることから
\(\hspace{10pt}h=\sqrt{3}\,\)
また底面となる\(\,\mathrm{△ABC}\,\)の面積\(\,S’\,\)は
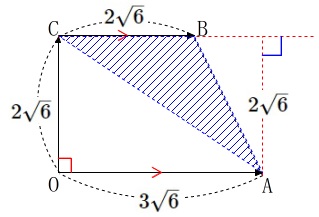台形\(\,\mathrm{OABC}\,\)の一部で
\(\begin{eqnarray}\displaystyle
S’&=&\frac{1}{2}\times \mathrm{CB}\times \mathrm{OC}\\
&=&\frac{1}{2}\times 2\sqrt{6}\times 2\sqrt{6}\\
&=&12
\end{eqnarray}\)
よって求める四面体\(\,\mathrm{DABC}\,\)の体積\(\,V\,\)は
\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times S\times h\\
&=&\frac{1}{3}\times 12\times \sqrt{3}\\
&=&\fbox{ 4 }\sqrt{\fbox{ 3 }}
\end{eqnarray}\)
以上です。
求め方はいろいろとありますが、普通に立つ方針かな？という方法で説明してみました。
センター試験や共通テストでは時間が足りないと感じる人が多いので、
あれこれ迷うより、思い立ったら突っ走る、方がはやいかもしれませんよ。
センター試験最後の問題でした。
次からは共通テストですね。
基本が大切だということは変わりませんよ。