3点を通る円の場合、円の方程式の形が決まっているので機械的に代入するだけで求めることができます。
そのため円に関係なく係数決定問題としてあつかうこともできますが、少し違った方針も立ててみましょう。
2点を通って中心が与えられた直線上にある円の方程式の求め方は、中心の設定がポイントです。
円の定義と円の方程式
円の定義からみておきましょう。
【円の定義】
中心となる1つの点から等距離にある点の集まりを円といいます。
中心から円周上の点までの距離を半径といいますが、半径が常に一定のもの、ということです。
円の方程式は中心と半径がわかれば求まります。
中心を \((a\,,\,b)\) , 半径を \( r\) とすると
\(\color{red}{(x-a)^2+(y-b)^2=r^2}\) ・・・①
これが標準形と呼ばれる円の方程式です。
これを展開して係数をわかりやすくおきかえ、
\( \color{red}{x^2+y^2+ax+by+c=0}\) ・・・②
としたものを一般形といいますが、円の方程式の形はどちらでもかまいません。
ただし、一般形で与えられた方程式から中心と半径を知りたいときは、標準形にした方が分かり易いので、標準形で目にする機会が多くなります。
円の方程式を求めるときは①②のどちらかを利用すれば求まります。
だから「円」というより係数決定問題とみても問題なく答は出るのです。
ただ、定義に沿って考えれば、
「中心と半径」
を求めれば円の方程式は求まるということがいえますので、大きな方針にしておくことは大切ですね。
1つ例題をあげて、いろいろな見方をしてみましょう。
3点を通る円の方程式の求め方
3点 \( (0\,,\,0),(-1\,,\,2),(4\,,\,-4)\) を通る円の方程式を求めよ。
実は円の方程式を求める問題では、この「3点を通る」という場合が一番計算量が多いです。
円は中心と半径があれば①の方程式
\( (x-a)^2+(y-b)^2=r^2\)
にあてはめるだけで良いのですが、3点が与えられる問題では中心も半径もわかりません。
\( x^2+y^2+ax+by+c=0\) ・・・②
を使うとしても決まっていない文字は3つです。
だから文字3つの連立方程式を解くことになるのです。
ちなみに、円の方程式を求めるときは大きく2つに分けられて、
・中心や半径のどちらか1つでも情報がある場合は標準形、
・単なる3点が与えられた場合は一般形、
から求めると早くなるのが普通です。
ここでは「3点」なので一般形に代入してみましょう。
標準形を利用するか、一般形を利用するかの2つありますがどちらでもかまいません。
円では標準形を利用する方が早い場合が多いですが、3点問題のときは6回の2乗の展開があるので一般形を利用すると比較的楽です。
\( x^2+y^2+ax+by+c=0\) に
\( (0\,,\,0)\) を代入すると \( c=0\) ・・・③
\( (-1\,,\,2)\) を代入すると
\( (-1)^2+(2)^2+a(-1)+b(2)+c=0\\ \\
\Leftrightarrow \hspace{5pt} 1+4-a+2b+c=0\)
整理して \( 5-a+2b+c=0\) ・・・④
\( (4\,,\,-4)\) を代入すると
\((4)^2+(-4)^2+a(4)+b(-4)+c=0\\ \\
\Leftrightarrow \hspace{5pt} 16+16+4a-4b+c=0\)
整理して \( 32+4a-4b+c=0\) ・・・⑤
③④⑤を解いて、
\( a=-21\,,\,b=-13\,,\,c=0\)
これが答じゃありません。
求めるものは円の方程式です。
\( \underline{x^2+y^2-21x-13y=0}\) ・・・(答)
代入しているというのは、「円がその点を通るから」ですよ。
円の方程式を求めるとき
\( (x-a)^2+(y-b)^2=r^2\)
を使うことが多いからといってこの3点問題に利用すると、
\( \begin{cases}
\hspace{5pt}(0-a)^2+(0-b)^2=r^2 \\
\hspace{5pt}(-1-a)^2+(2-b)^2=r^2 \\
\hspace{5pt}(4-a)^2+(-4-b)^2=r^2
\end{cases}\)
を解くことになります。
良いんですこれでも。ただ、分数になる場合、計算量はかなり増えます。
さらにこの問題を別の見方をすると、
「円の方程式は中心と半径がわかれば求まる」
ということから中心と半径を求めに行きます。
3点が円周上にあるということは、
円は3点でできる三角形の外接円です。
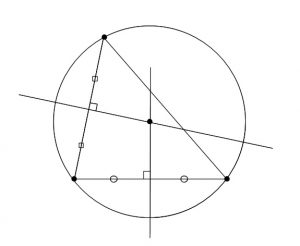
だから円の中心は三角形の各辺の垂直二等分線の交点になります。
幾何で知っていると思いますが垂直二等分線は2本で良いですよ。
3本目の交点も必ず一致しますから。
垂直二等分線の方程式を2本求めて連立すれば中心が求まるということです。
2点を通り中心が直線上にあるという円の方程式を求める問題
問題を先に見ましょう。
原点と点 \( (1\,,\,2)\) を通り、中心が直線 \( y=x+5\) 上にある円の方程式を求めよ。
この問題のポイントは「中心を文字で設定する」ことです。
後は円の方程式に必要な中心と半径を求めにいく、ということで条件をそろえれば求まります。
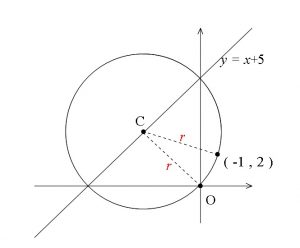
求める円の中心を \( C\) とすると、\( C\) は \( y=x+5\) 上にあるから
\( C(\,\color{red}{t}\,,\,\color{red}{t+5}\,)\)
とおけます。
半径を \( r\) とすると、円が原点を通ることから \( \color{red}{OC}\) が半径で
\( OC^2=t^2+(t+5)^2=r^2\)
よって円の方程式は
\( (x-\color{red}{t})^2+\left\{y-(\color{red}{t+5})\right\}^2=\color{red}{t^2+(t+5)^2}\) ・・・①
この円は \( (1\,,\,2)\) を通るから
\( (1-t)^2+\left\{2-(t+5)\right\}^2=t^2+(t+5)^2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (1-t)^2+(-3-t)^2=t^2+(t+5)^2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 1-2t+t^2+9+6t+t^2=t^2t^2+10t+25\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} -6t=15\)
これから
\( t=-\displaystyle \frac{5}{2}\)
①に代入すると
\( \left(x+\displaystyle \frac{5}{2}\right)^2+\left\{y-\left(-\displaystyle \frac{5}{2}+5\right)\right\}^2=\left(-\displaystyle \frac{5}{2}\right)^2+\left(-\displaystyle \frac{5}{2}+5\right)^2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \underline{\left(x+\displaystyle \frac{5}{2}\right)^2+\left(y-\displaystyle \frac{5}{2}\right)^2=\displaystyle \frac{25}{2}}\)
または、展開して一般形にした
\( \underline{x^2+y^2-5x-5y=0}\)
でも良いですよ。
標準形で出ているので中心と半径もすぐにわかります。
中心 : \(\displaystyle \left(-\frac{5}{2} , \frac{5}{2}\right)\)
半径 : \(\displaystyle \frac{5}{\sqrt{2}}=\frac{5\sqrt{2}}{2}\)
この解答では原点を通ることを先に使って処理しましたが、
半径を \(r\) として
\( (x-t)^2+\left\{y-(t+5)\right\}^2=r^2\)
これが原点と点 \( (1\,,\,2)\) を通るとしても良いですよ。
原点を通ることから
\( (-t)^2+(-t-5)^2=r^2\\ \\
\Leftrightarrow \hspace{5pt} t^2+t^2+10t+25=r^2\\ \\
\Leftrightarrow \hspace{5pt} 2t^2+10t+25=r^2 ・・・②\)
点 \( (1\,,\,2)\) を通ることから
\( (1-t)^2+\left\{2-(t+5)\right\}^2=r^2\\ \\
\Leftrightarrow \hspace{5pt} (1-t)^2+(-t-3)^2=r^2\\ \\
\Leftrightarrow \hspace{5pt} 1-2t+t^2+t^2+6t+9=r^2\\ \\
\Leftrightarrow \hspace{5pt} 2t^2+4t+10=r^2 ・・・③\)
②③を連立すると同じ
\( t=-\displaystyle \frac{5}{2}\)
が出てきます。
ポイントは中心の座標を文字を使って表したことにあります。
文字は増えるけど、2点があるので半径も文字でおけるということです。
直線上の定まっていない点を文字でおくというのは接線の問題でも良く使います。
1つの手法として覚えておきましょう。
図形と方程式は幾何の要素も含まれるので、幾何の復習もしておくといいです。
式である程度は処理できるので基本はしっかり復習しておきましょう。