整数の証明問題　必要条件と十分条件の違いと見分け方

整数をあつかいますが整数解などを求める単元ではなく、
整数の範囲での証明問題において論証をしてみようということです。
論証というと難しく聞こえますが、
必要条件や十分条件のことなので聞き慣れた言葉ではあるでしょう。
簡単に見分けることも出来ますのでしっかり取り組んでおきましょう。

必要条件と十分条件の違い

先ずは
「必要条件」と「十分条件」
ですね。

例えば、\( n\)　が正の数だとします。

「　\( n<1\) ならば　\( n^2<10\)　である。」

これは成り立ちます。

つまり
　\( n^2<10\)　であるためには　\( n<1\) ならば確かです。

この場合、「 \( n<1\) なら十分」となります。

　\( n<1\)　であるためには　\( n^2<10\)　でないと困ります。
この場合、「　\( n^2<10\)　が必要 」となります。

そこで一般に、「　\( p \Rightarrow q\)　」が成り立つとき、

　\(p\)　を　「 \( q\)　のための十分条件」
　\(q\)　を　「 \( p\) のための必要条件」

といいます。

上の例でいうと、
「 \( n<1 \Rightarrow n^2<10 \) 」が成立するので、

　\( n<1 \)　は　\( n^2<10\)　であるための十分条件
　\( n^2<10\)　は　\( n<1\)　であるための必要条件

です。

　\( p \Rightarrow q\)　が成り立つが、
　\( q \Rightarrow p\)　は成り立たないとき、

　「　\( p\)　は　\( q\)　であるための十分条件であるが、必要条件でない。」
　「　\( q\)　は　\( p\)　であるための必要条件であるが、十分条件でない。」

といいます。

さらに、\( p \Rightarrow q　,　 q \Rightarrow p\)　がともに成り立つとき、
　「　\( p \Leftrightarrow q\) 」と表し、

　「　\( p\)　は　\( q\)　であるための『必要十分条件』」

といい「 同値 」（記号：⇔）を意味します。

必要条件と十分条件の見分け方

「必要」なのか「十分」なのかを、
見分けるのが難しく感じる人もいるようですが、
図を使うと分かり易いです。

例題を交えてみてみましょう。

問題の A , B , C , D のどれであるかを調べるときは、
　\( p \rightarrow q　,　p\leftarrow q\)　のような記号を入れ、

右 → が成り立つときは「十分」、
左 ← が成り立つときは「必要」、

と○×を付けると分かりやすいと思いますよ。

「必要」と「十分」という言葉だけでは分かりにくいと思うので、
包含関係をおおざっぱに表すと、

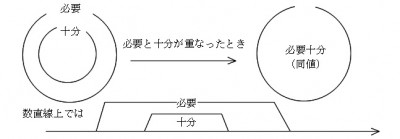
となっています。

問題を解いて行きましょう。
(1)　\( \alpha , \beta\)　が実数のとき，

　「　\( \alpha+\beta>0　,　\alpha\beta>0\)　」 は、
　「　\( \alpha>0　,　\beta>0\)　」であるための何条件か？

　「　\( \alpha+\beta>0　,　\alpha\beta>0 \rightarrow　\alpha>0　,　\beta>0 \)　」

を先ず見ます。

　\(\color{red}{ \alpha\beta>0}\)　から
　\(\color{red}{ \alpha , \beta} \)　は同符号（\( \pm\) が同じ）で、
(2つとも＋か、2つとも－でなければ、かけて＋にはならないから。）
　\(\alpha+\beta>0 \)　と合わせると　\(\alpha>0 , \beta>0 \)　です。

これから右向きの矢印 → は　○　です。

逆を見ると、
　\(\alpha+\beta>0　,　\alpha\beta>0　\leftarrow　\alpha>0 , \beta>0\)
ですが、
　\(\alpha>0 , \beta>0\)　なら　\(\alpha+\beta>0　,　\alpha\beta>0\)
は容易に成り立つことが分かります。

これから左向きの矢印　←　も　○　です。

したがって、
　\(\alpha+\beta>0　,　\alpha\beta>0 \Leftrightarrow \alpha>0　,　\beta>0\)
となり　Ａ（必要十分）。

(2)　\(\,x\,,\,y\,,\,z\,\)　が実数のとき、
　「　\( x^2+y^2+z^2=0\)　」 は
　「　\( x+y+z=0\)　」であるための何条件？

(1)とやり方は同じです。

　「　\(x^2+y^2+z^2=0 \rightarrow x+y+z=0\)　」

を見ます。

　\( x^2+y^2+z^2=0\)　のとき、
　\(\color{red}{ x=y=z=0}\)　しか実数は存在しません。
（ \( x^2 ≧ 0　,　y^2 ≧ 0　,　z^2 ≧ 0\)　なので）

よって

　\( x+y+z=0\)　が言えるので右 → は○です。

ところが　\(x+y+z=0\)　を満たす実数、
例えば、
　\( x=y=1,z=-2\)　のとき　\( x+y+z=0\)
ですが
　\(x^2+y^2+z^2=1+1+4\neq0\)
となり左 ← は×です。
（反例が１つでもあれば×）

したがって、

　\( x^2+y^2+z^2=0\)　は
　\( x+y+z=0\)　であるための

十分条件ではあるけど必要条件ではない。Ｃ（十分のみ）。

(3)　\( a,b,c\)　が実数のとき，
　\( ac>b^2\)　は
　\( x\)　のどのような実数値に対しても
　\( ax^2+2bx+c>0\)　であるための何条件か？

任意の　\( x\)　に対し、

　「 \( ac>b^2\)　ならば　\( ax^2+2bx+c>0\) 」

を調べるんですね。

２次方程式の解の判別式なので何となくはわかるでしょう。
ただ、問題に「２次」とは書いてないのです。

先ずは　\( ac>b^2 \rightarrow ax^2+2bx+c>0\)　です。

　\( ac>b^2\) において、\( a=0\)　のとき \( 0>b^2\) となり
実数 \(b\) は存在しなくなるので、\( a\neq 0\)　として良いです。

　\( a\neq 0\)の場合、右の２次関数が放物線であることから、
任意の \( x\) について
　\( ax^2+2bx+c>0 \)
（全ての点で \( x\) 軸より上）

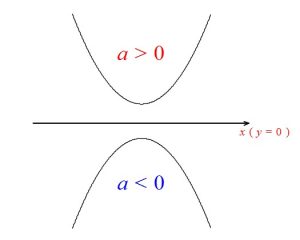
となるには
　\( a>0\) でなくてはなりません。

下に凸でなければ任意の \( x\) について
　\( ax^2+2bx+c>0\) は成り立たないからです。

例えば、
　\( a=-1,b=1,c=-4\) のとき \( ac>b^2\) ですが,
常に \( ax^2+2bx+c=-x^2+2x-4>0\)　とは言えません。

よって、右 → は×。
（反例：\(a=-1\,,\,b=1\,,\,c=-4\)　かつ　\(x=1\) のとき、
　\(ax^2+2bx+c=-x^2+2x-4=-1+2-4=-3<0\) ）
　
次に　\( ac>b^2 \leftarrow ax^2+2bx+c>0\)　です。

任意の \( x\) において \( ax^2+2bx+c>0\) となるのは、
大きく分けて２つの場合があります。

ⅰ) \( a>0\) のときで、かつ、
２次方程式 \( ax^2+2bx+c=0\) の解が存在しないとき。
（頂点の \(y\) 座標が \(x\) 軸より上にある。）

このとき、\( ax^2+2bx+c=0\) の判別式 \( D/4=b^2-ac\) において、
　\( D<0\) のときは \(ac\,>\,b^2\) なので○。

なのですが、

ⅱ) \( a=b=0\) のとき、\( c>0\) であれば、
任意の \(x\) において
　\(ax^2+2bx+c>0\) となりますが、
　\(b^2<ac\)　は成り立たないので×。

ⅱ)が反例となり、
ⅰ)のような場合は○だけど、ⅱ)で×となるので、左 ← は×になるのです。

よって、必要条件でも十分条件でもない、Ｄとなります。

反例をあげるだけならⅱ)だけでいいでしょう。
これは問題に「２次方程式、不等式」と書いてないので、
　\( a\) によって場合を考えないといけないのです。

「２次」と書いてあれば、\( a\neq 0\)　で考えて良いので少し楽になります。
このことは関数、方程式のところで集中して行きましょう。

整数とはあまり関係がありませんでしたが、
長くなったので整数部分の論証を次にまわします。

まとめ

必要条件、十分条件の見分け方は、

反例が１つでもあればダメ。

ということで「反例を探してから論証に入る」で良いと思いますよ。

⇒　整数と論証　倍数と類別と証明方法

「倍数である証明」も良く出ますね。