2021年(令和3年)度共通テストの数学ⅠAの問題と解説です。
初の実施となる大学入学共通テスト(共通テスト)は数学的な問題解決課程を重視するとセンターが方針を立てているため、
センター試験の60分から「考える時間」を考慮した70分の時間設定の変更がありました。
問題を見てすぐに分かることですが、考える時間を増やすというより、問題を読み取る時間を増やしたといった方が良いでしょう。
当然ですが数学の内容は変わっていません。
2021年(令和3年)度共通テストの数学ⅠAの問題
記述解答問題は公正な採点が困難ということから見送られました。
センター試験の問題よりページ数が増えることは予想通りです。
(最初のページや下書きページは削除してあります。)
2021年(令和3年)度共通テストの数学ⅠAの解説
グダグダな計画に受験生だけでなく学校の先生方も振り回され、
コロナ禍で、かつ厳しい寒波にある中で普通に受験できなかった人も多いでしょう。
傾向が変わったという声がたくさんありますが、
数学の問題への取り組み方を普段から普通に練習している人に取っては、
センター試験よりもやりやすく感じたかもしれません。
現役受験生はセンター試験は受けていないので、
変化を感じている人は少ないでしょう。
高校入試の近年の傾向がそうであるように、問題文の文字数は明らかに増えています。
10分長くなった試験時間ですがのんびりしているヒマはありませんね。
しつこいくらい問題が多いので簡単に解説していきます。
第1問
〔1〕
2次方程式
\(\hspace{4pt}2x^2+(4c-3)x+2c^2-c-11=0 ・・・①\)
を\(\,c\,\)について場合分けします。
(1)\(①\)において\(\,c=1\,\)のときです。
\(\hspace{4pt}2x^2+x-10=0 ・・・①’\)
左辺をタスキガケ因数分解すると
\(\hspace{10pt}2x^2+x-10\\
=(\color{black}{\fbox{ 2 }}x+\color{black}{\fbox{ 5 }})(x-\color{black}{\fbox{ 2 }})\)
このことから\(\,①’\,\)の解は
\(\begin{eqnarray}\displaystyle
2x^2+x-10&=&0\\
(2x+5)(x-2)&=&0\\
x&=&-\frac{5}{2}\,,\,2
\end{eqnarray}\)
となりますが方程式を解くことは求められていません。
因数分解できるかどうかを問われただけです。
(2)次は\(\,①\,\)において\(\,c=2\,\)のときの解を求めます。
\(\,c=2\,\)のとき\(\,①\,\)は
\(\hspace{4pt}2x^2+5x-5=0 ・・・①”\)
\(\,①”\,\)において解の公式から
\(\begin{eqnarray}\displaystyle
x&=&\frac{-5\pm \sqrt{5^2-4\cdot 2\cdot (-5)}}{2\cdot 2}\\
&=&\frac{-5\pm \sqrt{25+40}}{4}\\
&=&\frac{-\color{black}{\fbox{ 5 }}\pm \sqrt{\color{black}{\fbox{ 65 }}}}{\color{black}{\fbox{ 4 }}}
\end{eqnarray}\)
あれ?これって高校入試でしたっけ?
まあいいか。数学には違いない。
大きい方の解\(\,\alphaは\,\)
\(\hspace{10pt}\displaystyle \alpha=\frac{-5+\sqrt{65}}{4}\)
このとき
\(\begin{eqnarray}\displaystyle
\frac{5}{\alpha}&=&5\times \frac{1}{\alpha}\\
&=&5\times \frac{4}{\sqrt{65}-5}\\
&=&5\times \frac{4(\sqrt{65}+5)}{(\sqrt{65}-5)(\sqrt{65}+5)}\\
&=&5\times \frac{4(\sqrt{65}+5)}{65-25)}\\
&=&5\times \frac{4(\sqrt{65}+5)}{40}\\
&=&\frac{\sqrt{\color{black}{\fbox{65}}}+\color{black}{\fbox{5}}}{\color{black}{\fbox{2}}}
\end{eqnarray}\)
余計なことは考えず分母の有理化をすれば良いだけです。
また、\(\sqrt{65}\)は
\(\hspace{10pt}\color{red}{8}=\color{red}{\sqrt{64}}\)
\(\hspace{10pt}\color{blue}{9}=\color{blue}{\sqrt{81}}\)
なので、
\(\hspace{4pt}\color{red}{8}\,<\,\sqrt{65}\,<\,\color{blue}{9}\,\)
このことから
\(\begin{eqnarray}\displaystyle
\frac{5+\color{red}{8}}{2}<&\frac{5}{\alpha}&<\frac{5+\color{blue}{9}}{2}\\
6.5<&\frac{5}{\alpha}&<7
\end{eqnarray}\)
\(\,6.5\,\)と\(\,7\,\)の間にある数を整数で挟むと
\(\hspace{4pt}\displaystyle 6\,<\,\frac{5}{\alpha}\,<\,7\)
となるので、
\(\hspace{4pt}\displaystyle m<\frac{5}{\alpha}<m+1\)となる\(\,m\,\)は\(\color{black}{\fbox{ 6 }}\)です。
(3)\(\,①\,\)の解が異なる2つの有理数であるとき、
正の整数、つまり自然数である\(\,c\,\)の個数を求めます。
太郎さんと花子さんの会話はヒントですので、
なくても求める事はできるでしょう。
2次方程式の解が有理数ということは解の公式
\(\hspace{10pt}\displaystyle x=\frac{-b\pm \sqrt{D}}{2a}\)
において根号の中身、つまり判別式(判定式)が平方数となれば良いのですが、
「有理数の解である」ということは「実数解でなくてはならない」、
ということでもあります。
\(\begin{eqnarray}\displaystyle
D&=&(4c-3)^2-4\cdot 2(2c^2-c-11)\\
&=&16c^2-24c+9-16c^2+8c+88\\
&=&-16c+97
\end{eqnarray}\)
これから実数解であるための条件は
\(\begin{eqnarray}\displaystyle
-16c+97&>&0\\
-16c&>&-97\\
c&<&\frac{97}{16}=6.0625
\end{eqnarray}\)
このことから\(\,c\,\)は自然数なので\(\,1\,\)から\(\,6\,\)までの6つを調べれば良いことになります。
(割り算は\(\,6.\cdots\,\)となることが分かった時点で計算する必要はありません。)
\(\,c=1\,\)のときは(1)で有理数の解だと分かっています。
\(\,c=2\,\)のときは(2)で無理数の解だと分かっています。
\(\,c=3\,\)のとき
\(\begin{eqnarray}\displaystyle
D&=&-16\times 3+97\\
&=&49 (平方数)
\end{eqnarray}\)
\(\,c=4\,\)のとき
\(\begin{eqnarray}\displaystyle
D&=&-16\times 4+97\\
&=&33 (平方数ではない)
\end{eqnarray}\)
\(\,c=5\,\)のとき
\(\begin{eqnarray}\displaystyle
D&=&-16\times 5+97\\
&=&17 (平方数ではない)
\end{eqnarray}\)
\(\,c=6\,\)のとき
\(\begin{eqnarray}\displaystyle
D&=&-16\times 6+97\\
&=&1 (平方数)
\end{eqnarray}\)
よって、
\(\,c=1\,,\,3\,,\,6\,\)
のときに有理数の解になります。
答え \(\color{black}{\fbox{ 3 }}\)個
〔2〕
三角比を利用した具体的な計算と一般的な性質です。
参考図が与えられていて、
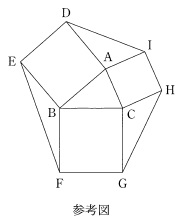
三角形の対辺を
\(\,\mathrm{BC}=a\,,\,\mathrm{CA}=b\,,\,\mathrm{AB}=c\,\)
とし、角度をそれぞれ、
\(\,\mathrm{∠CAB}=A\,,\,\mathrm{∠ABC}=B\,,\,\mathrm{∠BCA}=C\,\)
とします。
(習慣なのでいつも通りに見ていけば良いです。)
ただし、それぞれの対辺で正方形がつくられているので、
三平方の定理を証明するときの図に似ています。
では、問題を見ていきましょう。
(1)
\(\hspace{4pt}\displaystyle \,b=6\,,\,c=5\,,\,\cos A=\frac{3}{5}\,\)のとき、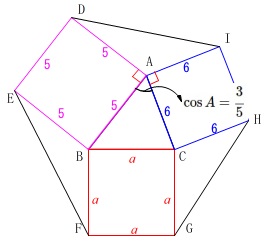
\(\begin{eqnarray}\displaystyle
\sin^{2}A&=&1-\cos^{2}A\\
&=&1-\left(\frac{3}{5}\right)^2\\
&=&\frac{16}{25}\\
\sin A&=&\frac{\color{black}{\fbox{ 4 }}}{\color{black}{\fbox{ 5 }}} (\sin A>0\,)
\end{eqnarray}\)
このときは\(\,\mathrm{△ABC}\,\)が二等辺三角形になりますが関係ありません。
面積の公式から
\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\,b\,c\,\sin A\\
&=&\frac{1}{2}\times 6\times 5\times \frac{4}{5}\\
&=&\color{black}{\fbox{ 12 }}
\end{eqnarray}\)
また、\(\,\mathrm{∠BAD=∠CAI=90^{\circ}}\,\)なので、
\(\begin{eqnarray}
\mathrm{∠DAI+∠BAC}&=&180^{\circ}\\
\mathrm{∠DAI}&=&180^{\circ}-\mathrm{∠BAC}\\
&=&180^{\circ}-A
\end{eqnarray}\)
 であることから
であることから
\(\hspace{4pt}\sin \mathrm{∠DAI}=\sin A\)
よって、\(\,\mathrm{△AID}\,\)の面積は\(\,\mathrm{△ABC}\,\)と同じになります。
\(\begin{eqnarray}\displaystyle
\mathrm{△AID}&=&\frac{1}{2}\,b\,c\,\sin \mathrm{∠DAI}\\
&=&\frac{1}{2}\,b\,c\,\sin A\\
&=&\frac{1}{2}\times 6\times 5\times \frac{4}{5}\\
&=&\color{black}{\fbox{ 12 }}
\end{eqnarray}\)
(2)
余弦定理
\(\hspace{10pt}a^2=b^2+c^2-2\,b\,c\,\cos A\)
を利用して考えなさい、ということでしょう。
正方形の面積はそれぞれ
\(\begin{eqnarray}\displaystyle
S_1&=&a^2\\
S_2&=&b^2\\
S_3&=&c^2
\end{eqnarray}\)
なので余弦定理から
\(\hspace{10pt}S_1=S_2+S_3-2\,b\,c\,\cos A\)
問題の値にするために移項すると
\(\hspace{10pt}\color{red}{S_1-S_2-S_3}=-2\,b\,c\,\cos A\)
・\(\,0^{\circ}\,<\,A\,<\,90^{\circ}\,\)のとき\(\hspace{4pt}\cos A\,>\,0\)
だから右辺は
\(\hspace{4pt}-2\,b\,c\,\cos A\,<\,0\)
答え \(\color{black}{\fbox{ ト }}\) \(\,\underline{ ② }\,\)
・\(\,A=90^{\circ}\,\)のとき\(\hspace{4pt}\cos A=0\,\)
なので右辺は
\(\hspace{4pt}-2\,b\,c\,\cos A\,=\,0\)
答え \(\color{black}{\fbox{ ナ }}\) \(\underline{ ⓪ }\)
・\(\,90^{\circ}\,<\,A\,<\,180^{\circ}\,\)のとき\(\hspace{4pt}\cos A\,<\,0\)
だから右辺は
\(\hspace{4pt}-2\,b\,c\,\cos A\,>\,0\)
答え \(\color{black}{\fbox{ ニ }}\) \(\,\underline{ ① }\,\)
三平方の定理を思い出すと、
\(\,\cos A=90^{\circ}\,\)
のとき、つまり直角三角形において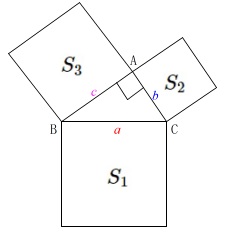
\(\hspace{10pt}a^2=b^2+c^2\)
が成り立つので
\(\hspace{10pt}S_1-S_2-S_3=0\)
はすぐに分かります。
\(\,0^{\circ}\,<\,A\,<\,90^{\circ}\,\)のとき、
対辺となる\(\,a\,\)は\(\,A=90°\,\)のときより\(\,b\,,\,c\,\)に対して短くなるので、
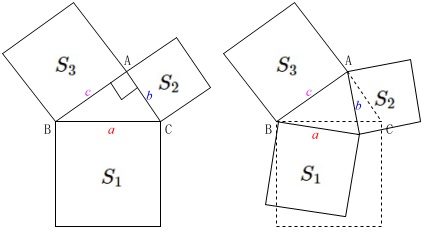
直感的にですが
\(\hspace{10pt}a^2<b^2+c^2\)
になることは分かるでしょう。
\(\hspace{4pt}S_1-S_2-S_3<0\)
逆に\(\,A\,\)が鈍角のときは対辺\(\,a\,\)が\(\,b\,,\,c\,\)に対して長くなるので
\(\hspace{4pt}S_1-S_2-S_3>0\)
ちなみに「\(\,a\,\)が\(\,b\,,\,c\,\)に対して」というのは、
\(\,a\,\)が\(\,b,c\,\)より短くなる、長くなるということではありません。
例えば、\(\,b\,,\,c\,\)を固定して見れば\(\,a\,\)は\(\,90°\,\)のときより短い、長いという判断ができるということです。
直角三角形の場合の図を書いて、
\(\,A=90°\,\)の場合から考えれば余弦定理でなくても答えは出たと思います。
(3)
これは(1)の途中ですでに示しています。
\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\,b\,c\,\sin A\\
&=&\frac{1}{2}\,b\,c\,\sin (180^{\circ}-A)\\
&=&\frac{1}{2}\,b\,c\,\mathrm{∠DAI}\\
&=&\mathrm{△AID}=T_1
\end{eqnarray}\)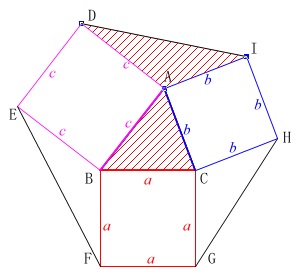 同様に、
同様に、
\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\,a\,c\,\sin B\\
&=&\frac{1}{2}\,a\,c\,\sin (180^{\circ}-B)\\
&=&\frac{1}{2}\,a\,c\,\mathrm{∠EBF}\\
&=&\mathrm{△BEF}=T_2
\end{eqnarray}\)
また、
\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\,a\,b\,\sin C\\
&=&\frac{1}{2}\,a\,b\,\sin (180^{\circ}-C)\\
&=&\frac{1}{2}\,a\,b\,\mathrm{∠GCH}\\
&=&\mathrm{△CGH}=T_3
\end{eqnarray}\)
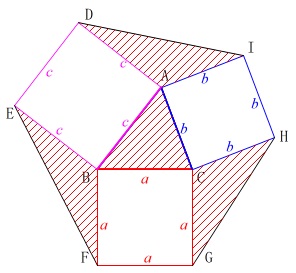
これは\(\,a\,,\,b\,,\,c\,\)関係無しに成り立つ関係なので、
\(\hspace{4pt}T_1=T_2=T_3\)
答え \(\color{black}{\fbox{ ヌ }}\) \(\,\underline{ ③ }\,\)
この関係は図形で見ると、
 \(\,T_1\,,\,T_2\,,\,T_3\,\)がそれぞれの場合で、
\(\,T_1\,,\,T_2\,,\,T_3\,\)がそれぞれの場合で、
\(\,\mathrm{△ABC}\,\)と底辺と高さが同じで面積が等しくなるからです。
\(\,T_1\,,\,T_2\,,\,T_3\,\)の直接の比較は難しいですが、
\(\,\mathrm{△ABC}\,\)の面積と等しいことは、
(1)で\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△AID}\,\)の面積を求めたときに同じになるので、
ヒントになってくれたのではないでしょうか。
(4)
次は外接円の半径です。(まだ続くのか。)
\(\hspace{4pt}\displaystyle 2R=\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)
正弦定理で考えましょう。
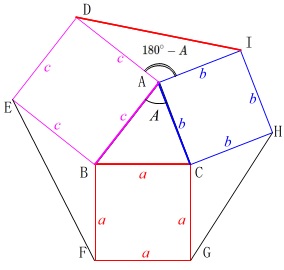 \(\hspace{4pt}0^{\circ}\,<\,A\,<\,90^{\circ}\,\)のとき、
\(\hspace{4pt}0^{\circ}\,<\,A\,<\,90^{\circ}\,\)のとき、
\(\,\mathrm{△AID}\,\)と\(\,\mathrm{△ABC}\,\)において
\(\,b\,,\,c\,\)は変わらず\(\mathrm{∠DAI}\,\)は鈍角になるので、
\(\,\mathrm{ID}\,\)\(\color{black}{\fbox{ > }}\)\(\,\mathrm{BC}\,\)
このとき外接円の半径は\(\,\mathrm{△AID}\,\)の方が大きくなります。
直感的にも分かりますが正弦定理から、
\(\,\mathrm{△AID}\,\)の外接円の半径\(\,\mathrm{R_{△AID}}\,\)は
\(\hspace{4pt}\displaystyle \mathrm{R_{△AID}}=\frac{\mathrm{ID}}{2\,\sin (\,180^{\circ}-A\,)}=\frac{\mathrm{ID}}{2\,\sin A}\)
\(\,\mathrm{△ABC}\,\)の外接円の半径\(\,\mathrm{R_{△ABC}}\,\)は
\(\hspace{4pt}\displaystyle \mathrm{R_{△ABC}}=\frac{\mathrm{BC}}{2\,\sin A}\)
で分母は同じで分子が\(\,\mathrm{ID}\,\)>\(\,\mathrm{BC}\,\)なので
\(\,\mathrm{R_{AID}}\,\)\(\color{black}{\fbox{ > }}\)\(\,\mathrm{R_{△ABC}}\,\)
問題文の「であるから」という誘導通り、
これがヒントになって外接円の半径が最も小さい場合を考えます。
・\(\,0^{\circ}<A<B<C<90^{\circ}\,\)のときは、
補角となる
\(180^{\circ}-A\,,\,180^{\circ}-B\,,\,180^{\circ}-C\)
はすべて鈍角となるので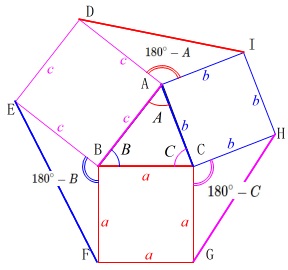 \(\,\mathrm{△AID\,,\,△BEF\,,\,△CGH}\,\)の外接円の半径は、
\(\,\mathrm{△AID\,,\,△BEF\,,\,△CGH}\,\)の外接円の半径は、
\(\,\mathrm{△ABC}\,\)の外接円の半径より大きくなります。
よって、
最も外接円の半径が小さいのは\(\,\mathrm{△ABC}\,\)です。
答え \(\color{black}{\fbox{ ハ }}\) \(\,\underline{ ⓪ }\,\)
・\(\,0^{\circ}<A<B<90^{\circ}<C\,\)のときは、
\(\,C\,\)の補角\(\,180^{\circ}-C\,\)が鋭角となるので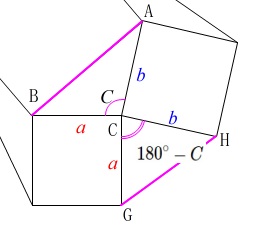
\(\,\mathrm{AB}\,\)>\(\,\mathrm{GH}\,\)
このとき外接円の半径は
\(\displaystyle \frac{\mathrm{AB}}{2\,\sin C}>\frac{\mathrm{GH}}{2\,\sin C}\)
から
\(\,\mathrm{R_{△ABC}}\,\)>\(\,\mathrm{R_{△CGH}}\,\)
\(\,\mathrm{△AID}\,\)と\(\,\mathrm{△BEF}\,\)の外接円の半径は、
\(\,\mathrm{△ABC}\,\)の外接円の半径より大きいので、
最も外接円の半径が小さいのは\(\,\mathrm{△CGH}\,\)となります。
答え \(\color{black}{\fbox{ ヒ }}\) \(\,\underline{ ③ }\,\)
第1問はここまでです。
第2問
第2問だけで\(\,13\,\)ページあります。
〔1〕\(\,100\,m\,\)走のタイムに関係する問題です。
(時間と速さと道のりの関係と関数の問題。)
ストライドは\(\,1\,\)歩で進む距離
ピッチは\(\,1\,\)秒間に動く歩数
という説明をするための\(\,1\,\)ページ目です。
ストライドとピッチの単位は
ストライド:\(\displaystyle \frac{\color{red}{m}}{\color{blue}{歩}}\)
ピッチ:\(\displaystyle \frac{\color{blue}{歩}}{\color{magenta}{秒}}\)
この単位をかけると
\(\displaystyle \frac{\color{red}{m}}{\color{blue}{歩}}\times \frac{\color{blue}{歩}}{\color{magenta}{秒}}=\frac{\color{red}{m}}{\color{magenta}{秒}}\)
となり\(\,1\,\)秒間当たりに進む距離、つまり平均速度になります。
(1)
ストライドを\(\,x\,\)
ピッチを\(\,z\,\)
とおくと、
平均速度は\(\,xz\,\)
です。
答え \(\color{black}{\fbox{ ア }}\) \(\,\underline{ ② }\,\)
答えは選択肢の中にあるので、
単位が速さになるものを選んでも良いですが、
\(\,⑤\,\)は何故\(\,2\,\)で割るのか意味が分からなくなります。
(平均だから?平均は足して割る、ですよね。)
ここでタイムは平均速度で距離\(\,100\,m\,\)を割れば求まります。
\(\displaystyle \,タイム=\frac{100}{xz}\, ・・・①\)
小学生の道のりと速さと時間の関係と同じです。
(2)普通に考えれば分かりますが、
ピッチを同じにできるなら、
ストライドを大きくすることでタイムは良くなります。
\(\,1\,\)秒間の歩数が同じで、
歩幅が大きくなると速く移動できますよね。
実際にはストライドを大きくするとピッチは落ちます。
なのでストライドを大きくするかピッチを速くするか、
どのくらいのストライドでどのくらいのピッチになっていれば、
最もいいタイムになるかを計測データから探していきます。
\(\begin{array}{|c|c|c|c|c|} \hline
& \, 1\,回目 &\, 2\,回目 & \,3\,回目 \\ \hline
ストライド(\, x\,) & 2.05 & 2.10 & 2.15 \\ \hline
ピッチ(\,z\,) & 4.70 & 4.60 & 4.50 \\ \hline
\end{array}\)
この表の値から、
ピッチ\(\,z\,\)がストライド\(\,x\,\)の\(\,1\,\)次関数と仮定したそうです。
つまり、\(\,(\,x\,,\,z\,)\,\)の\(\,2\,\)点を通る直線の式を求めれば良いということです。
どの\(\,2\,\)点でも良いですが、
\(\,(\,2.05\,,\,4.70\,)\,\)
\(\,(\,2.15\,,\,4.50\,)\,\)
を通る\(\,1\,\)次関数は変化の割合(傾き)が
\(\displaystyle \frac{4.50-4.70}{2.15-2.05}=-2\)
なので
\(\displaystyle z=\color{black}{\fbox{ -2 }}\,x+\frac{\color{black}{\fbox{ 44 }}}{5} ・・・②\)
もちろんストライドもピッチも限界があります。
ここでは(太郎さんの場合)
ストライド\(\,x\,\)の最大値は\(\,2.40\,\)
ピッチ\(\,z\,\)の最大値は\(\,4.80\,\)
となっています。
ピッチが最大になるときストライドは最小になるので、
\(\,②\,\)に\(\,z=4.80\,\)を代入すると
\(\begin{eqnarray}\displaystyle
4.80&=&-2\,x+\frac{44}{5}\\
x&=&2.00\\
\end{eqnarray}\)
これがストライド\(\,x\,\)の最小値となります。
最大値は与えられているので
\(\hspace{4pt}\color{black}{\fbox{ 2 }}.\color{black}{\fbox{ 00 }}\,≦\,x\,≦\,2.40\)
続きです。
\(\hspace{4pt}y=xz\)
とおくと、
\(\hspace{4pt}\displaystyle z=-2\,x+\frac{44}{5} ・・・②\)
なので、
\(\begin{eqnarray}\displaystyle
y&=&x\left(-2\,x+\frac{44}{5}\right)\\
&=&-2x^2+\frac{44}{5}x\\
&=&-2\left(x^2-\frac{22}{5}\,x\right)\\
&=&-2\left(x-\frac{11}{5}\right)^2+2 \times \frac{11^2}{5^2}
\end{eqnarray}\)
よって、\(\,y\,\)が最大になる\(\,x\,\)は、
\(\hspace{4pt}2.00\,≦\,x\,≦\,2.40\)
であることも考えて、
\(\displaystyle \,x=\frac{11}{5}=\color{black}{\fbox{ 2.20 }}\,\)
のときです。
ここは問題に「\(\,②\,\)を\(\,y\,\)に代入することにより」と書いてあるので問題ないでしょう。
タイムは
\(\displaystyle \,タイム=\frac{100}{xz}\, ・・・①\)
から分母が大きいほど小さくなる、
つまり、\(\,xz\,\)が最大のとき一番良くなるので、
\(\,x=2.20\,\)のとき最もいいタイムとなります。
このときピッチ\(\,(\,z\,)\,\)は
\(\begin{eqnarray}\displaystyle
z&=&-2\,x+\frac{44}{5}\\
&=&-2\times 2.20+\frac{44}{5}\\
&=&-4.40+8.80\\
&=&\color{black}{\fbox{ 4.40 }}
\end{eqnarray}\)
また、このときのタイムは
\(\displaystyle \frac{100}{2.20\times 4.40}=\underline{ 10.33 }\)
答え \(\color{black}{\fbox{ ソ }}\) \(\,\underline{ ③ }\,\)
問題で指示された式を見ながら代入していくだけで答えが出ます。
〔2〕データの分析です。
(1)24個の箱ひげ図があります。
それぞれは47の都道府県のデータの箱ひげ図です。
例えば2010年の箱ひげ図は3つありますが、
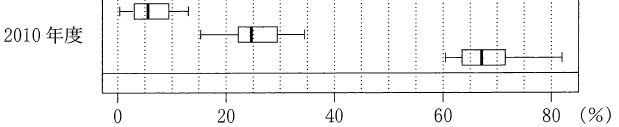
一番上の箱ひげ図は第1次産業の就業者が、
最小値の0%程度というどこかの都道府県があり、
最大値の13%程度の他の都道府県があり、
中央値となる6%程度の都道府県があるということを意味しています。
2番目は第2次産業就業者の箱ひげ図、
一番下は第3次産業就業者の箱ひげ図です。
もちろん箱ひげ図なので、
中央値から左側と右側にはそれぞれ23県分のデータがあります。
ということが1ページ目と2ページ目に説明がされています。
24個の箱ひげ図の中で正しくないものを2つ探します。
\(\,⓪\,\)『第1次産業の就業者数割合の四分位範囲は2020年度までは、
後の時点になるに従って減少している。』
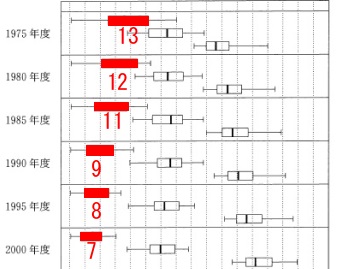 ざっくりと読み取っても正しい。
ざっくりと読み取っても正しい。
四分位範囲は第3四分位数と第1四分位数との差です。
(箱となっている長方形の横(左右側)の長さです。)
\(\,①\,\)『第1次産業の就業者数割合について、ひげはどの時点(年度)においても左側が長い。』
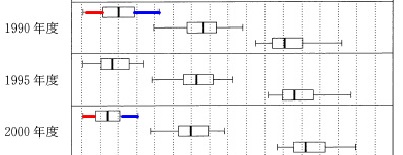 右側が長い年度もあります。
右側が長い年度もあります。
正しくない。
\(\,②\,\)『第2次産業の就業者数割合の中央値は、1990年度以降減少している。』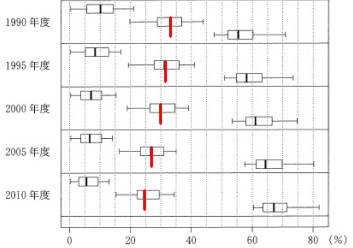 正しい。
正しい。
\(\,③\,\)『第2次産業の就業者数割合の第1四分位数は、後の時点になるにしたがって減少している。』
 1900年度までは増加している年度もあると言えます。
1900年度までは増加している年度もあると言えます。
正しくない。
答え \(\color{black}{\fbox{ タ }}\) \(\,\underline{ ① }\,\) \(\color{black}{\fbox{ チ }}\) \(\,\underline{ ③ }\,\)
答えは2つ出そろいましたが一応後も見ておきます。
\(\,④\,\)『第3次産業の就業者数割合の第3四分位数は、後の時点になるにしたがって増加している。』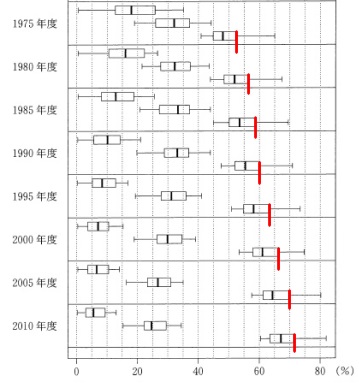 正しい。
正しい。
\(\,⑤\,\)『第3次産業の就業者数割合の最小値は、後の時点になるにしたがって増加している。』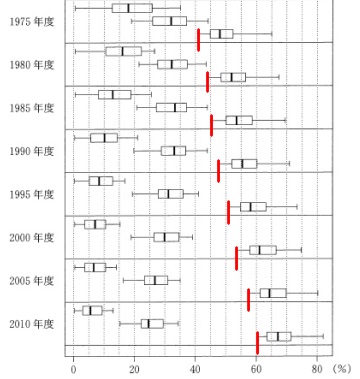 正しい。
正しい。
ここは箱ひげ図の用語の確認だけなので説明は必要ないでしょう。
ちなみに箱ひげ図は中学生の内容になります。
(2)\(\,8\,\)時点から\(\,5\,\)時点を取り出してヒストグラムにしてあります。
5年ごとの\(\,8\,\)回分のデータから\(\,5\,\)回分を取り出しているということですよ。
ヒストグラムにしてあるのは第1次産業と第3次産業の就業者数割合です。
箱ひげ図から読み取れることを書き出しておきます。
値の読み取りは、
「以上」、「未満」が読み取れる範囲で、
どちらの階級に含まれるかの判断がつけば良いです。
・1985年度は、
第1次産業就業者数割合について
最小値:0%
中央値:13%
最大値:26%
第3次産業就業者数割合について
最小値:45%
中央値:53%
最大値:69%
これを満たすヒストグラム(グラフ)は\(\,\underline{ ① }\,\)だけです。
問題でも説明してくれていますが、
45%は『45%以上50%未満の階級』に入ります。
・1995年度は、
第1次産業就業者数割合について
最小値:0%
中央値:8%
最大値:17%
第3次産業就業者数割合について
最小値:51%
中央値:58%
最大値:73%
これを満たすグラフは\(\,\underline{ ④ }\,\)だけです。
答え \(\color{black}{\fbox{ ツ }}\) \(\,\underline{ ① }\,\) \(\color{black}{\fbox{ テ }}\) \(\,\underline{ ④ }\,\)
ヒストグラムの度数は、
中央値が最小値から数えて24県目の都道府県、
であることを見ておけば良いです。
(3)散布図です。
図\(\,2\,\)は1975年度の散布図です。
見方は説明する必要もないと思いますが、
例えば、第1次産業と第3次産業の散布図で、
右端に2つの点がありますが、
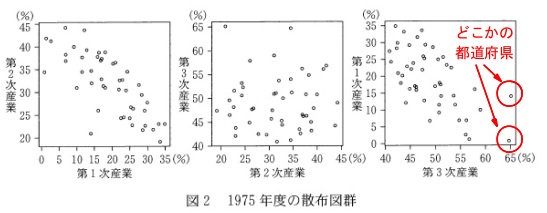 どちらも第3次産業の就業者数割合が65%程度で、
どちらも第3次産業の就業者数割合が65%程度で、
第1次産業の就業者数割合0%に近い都道府県と、
第1次産業の就業者数割合15%に近い都道府県とがあるということです。
つまり、点はそれぞれの散布図で47個あります。
1975年度を基準にしたとき、
2015年度の相関が強くなったかどうか正しい組み合わせを選びます。
相関は正でも負でもまとまりが直線に近づくほど強いことを意味します。
\(\,\mathrm{(Ⅰ)}\,\)第1次産業と第2次産業の就業者数割合の間の相関は、
 ばらつきが大きくなっているので相関は強くなっていません。
ばらつきが大きくなっているので相関は強くなっていません。
\(\,\mathrm{(Ⅱ)}\,\))第2次産業と第3次産業の就業者数割合の間の相関は、
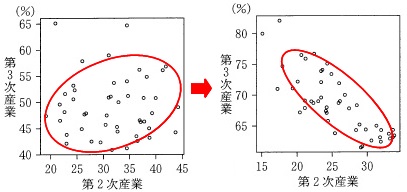 1975年度よりは相関が強くなっています。
1975年度よりは相関が強くなっています。
\(\,\mathrm{(Ⅲ)}\,\))第3次産業と第1次産業の就業者数割合の間の相関は、
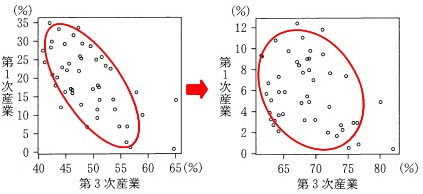 ばらつきが大きくなっているので相関は強くなっていません。
ばらつきが大きくなっているので相関は強くなっていません。
答え \(\color{black}{\fbox{ ト }}\) \(\,\underline{ ⑤ }\,\)
まだあります。
(4)第1次産業就業者割合の散布図を選びますが、
どの産業でも構いません。
横軸は就業者数割合で同じなので、
1つの男性の就業者数割合の散布図から女性の割合を出せば良いだけです。
例えば、
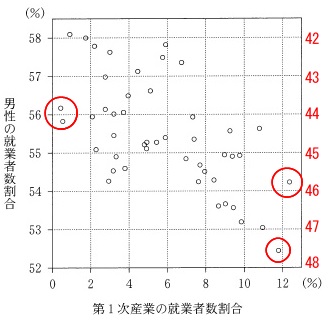 就業者数割合が\(\,0\,\)%近いところで、
就業者数割合が\(\,0\,\)%近いところで、
男性が\(\,56\,\)%前後に2つの都道府県があり、
男性女性合わせると\(\,100\,\)%になることから、
女性の就業者数割合は\(\,44\,\)%前後に2つの都道府県があることになります。
就業者数割合が高いところで見ると、
男性が\(\,54\,\)%くらいの都道府県の女性の就業者数割合は\(\,46\,\)%、
男性が\(\,52.5\,\)%くらいの都道府県では女性の就業者数割合は\(\,47.5\,\)%となります。
簡単に言ってしまうと、
男性\(\,55\,\)%女性\(\,45\,\)%の軸で上下逆さまにしたものが、
女性の就業者数割合の散布図になります。
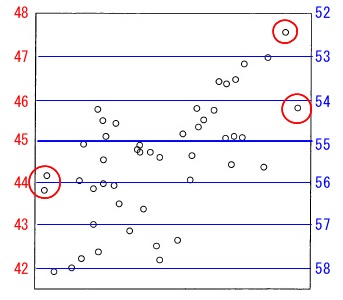
答え \(\color{black}{\fbox{ ナ }}\) \(\,\underline{ ② }\,\)
これで必答問題が終わりです。
⇒ 2021年(令和3年)度共通テストの数学ⅠAの選択問題と解説
次は選択問題ですが、
どの\(\,2\,\)問を選択するかは人によって違うのでここでいったん区切ります。
センター試験とは分量が違いますが、
内容は2021年度の問題は決して難しいとは言えない程度です。
センター試験の問題には目を通しておいた方が良いですね。
確かに慣れていなければ教科書のように機械的に解ける問題ではないかもしれませんが、
数学の内容が変わっているわけではありません。