2021年(令和3年)度共通テストの数学ⅠＡの選択問題と解説

２０２１年(令和３年)度共通テストの数学ⅠＡの選択問題の解説です。
選択問題は第３問の確率と第４問の整数と第５問の幾何の３問から２問を選択します。
いずれもヒントとなる誘導がありますが、必答問題で時間が必要でじっくり考える時間はあまりなかったかもしれません。

２０２１年(令和３年)度共通テストの数学ⅠＡの選択問題

選択問題だけのページを抜き取ってあります。

⇒　２０２１年度共通テスト数学１Ａの選択問題

第１問と第２問は必答問題の解説ページにあります。
（後でリンクさせておきます。）

２０２１年(令和３年)度共通テストの数学ⅠＡの選択問題の解説

第３問は確率、第４問は整数、第５問は幾何です。
受験前にはある程度決めて対策しているでしょう。
今回は、幾何が一番ページ数と日本語の文字数は少ないです。笑

第３問（選択問題）

『くじ引きの結果から、どの箱からくじを引いた可能性が高いか条件付き確率で考える。』
問題だそうです。

(1)箱が２種類ある場合を考えます。

　くじが当たる確率\(\,\displaystyle \frac{1}{2}\,\)の箱\(\,\mathrm{A}\,\)
と
　くじが当たる確率\(\,\displaystyle \frac{1}{3}\,\)の箱\(\,\mathrm{B}\,\)
の場合です。

(\(\,\mathrm{ⅰ}\,\))
引いたくじを元に戻す試行を３回繰り返したとき、
３回中１回あたる確率を求めます。

箱\(\,\mathrm{A}\,\)でも箱\(\,\mathrm{B}\,\)でも３回中１回当たる場合は、
　\(\begin{array}{|c|c|c|} \hline
１回目 & ２回目 & ３回目 \\ \hline
○ & × & × \\ \hline
× & ○ & × \\ \hline
× & × & ○ \\ \hline
\end{array}\)
何回目に当たるかで３通りあります。
　\(\mathrm{_{3}C_{1}}=3\)

１回当たるということは２回はずれくじを引くということなので、
箱\(\,\mathrm{A}\,\)において３回中１回当たる確率は
　\(\hspace{10pt}\displaystyle \mathrm{_{3}C_{1}}\times \left(\frac{1}{2}\right)^1\times \left(\frac{1}{2}\right)^2\\
\displaystyle =3\times \frac{1}{2}\times \frac{1}{4}\\
\displaystyle =\frac{\color{black}{\fbox{　3　}}}{\color{black}{\fbox{　8　}}}\)

同様に箱\(\,\mathrm{B}\,\)で３回中１回当たる確率は、
外れくじを引く確率が\(\,\displaystyle \frac{2}{3}\,\)であることから、
　\(\hspace{10pt}\displaystyle \mathrm{_{3}C_{1}}\times \left(\frac{1}{3}\right)^1\times \left(\frac{2}{3}\right)^2\\
\displaystyle =3\times \frac{1}{3}\times \frac{4}{9}\\
\displaystyle =\frac{\color{black}{\fbox{　4　}}}{\color{black}{\fbox{　9　}}}\)

(\(\,\mathrm{ⅱ}\,\))
３回中１回当たりくじを引くのは、
　箱\(\,\mathrm{A}\,\)を選んで３回中１回当たり
　箱\(\,\mathrm{B}\,\)を選んで３回中１回当たり
の２つの場合があります。

　箱\(\,\mathrm{A}\,\)が選ばれる事象を\(\,A\,\)
　箱\(\,\mathrm{B}\,\)が選ばれる事象を\(\,B\,\)
　３回中ちょうど１回あたる事象を\(\,W\,\)
とすると、
　\(\,P(A\,\mathrm{\cap}\,W)\,\)は
　「\(\,\mathrm{A}\,\)が選ばれて、かつ、３回中１回当たり」
を意味します。

「\(\,\mathrm{A}\,\)を選ぶ確率\(\,P(A)\,\)は、
箱は\(\,\mathrm{A}\,\)か\(\,\mathrm{B}\,\)しかないので、
　\(\hspace{10pt}\displaystyle P(A)=\frac{1}{2}=P(B)\,\)

さらに箱\(\,\mathrm{A}\,\)で３回中１回あたる確率は(\(\,\mathrm{ⅰ}\,\))から\(\,\displaystyle \frac{3}{8}\,\)だったので、
　\(\hspace{10pt}\begin{eqnarray}\displaystyle
\color{red}{P(A\,\cap\,W)}&=&\frac{1}{2}\times \frac{3}{8}
\end{eqnarray}\)

同様に箱\(\,\mathrm{B}\,\)を選んで３回中１回あたる確率は、
　\(\hspace{10pt}\begin{eqnarray}\displaystyle
\color{blue}{P(B\,\cap\,W)}&=&\frac{1}{2}\times \frac{4}{9}
\end{eqnarray}\)
である。」ということが問題に書いてあります。

また、３回中１回当たりを引く確率\(\,P(W)\,\)は、
　箱\(\,\mathrm{A}\,\)を選んで３回中１回当たり
　箱\(\,\mathrm{B}\,\)を選んで３回中１回当たり
の２つの場合があるので
　\(\begin{eqnarray} \displaystyle
\color{magenta}{P(W)}&=&P(A\,\cap\,W\,)+P(B\,\cap\,W)\\
&=&\frac{1}{2}\times \frac{3}{8}+\frac{1}{2}\times \frac{4}{9}\\
&=&\frac{1}{2}\left(\frac{3}{8}+\frac{4}{9}\right)\\
&=&\frac{1}{2}\times \frac{27+32}{72}\\
&=&\frac{1}{2}\times \frac{59}{72}
\end{eqnarray}\)　

ここで、
　「３回中１回当たったとき、選んだ箱が\(\,A\,\)である条件付き確率」
となる\(\,P_W(A)\,\)は、
　\(\begin{eqnarray}\displaystyle
P_W(A)&=&\frac{\color{red}{P(A\cap W)}}{\color{magenta}{P(W)}}\\
&=&\frac{\frac{1}{2}\times \frac{3}{8}}{\frac{1}{2}\times \frac{59}{72}}\\
&=&\left(\frac{1}{2}\times \frac{3}{8}\right)\div \left(\frac{1}{2}\times \frac{59}{72}\right)\\
&=&\frac{3\times 72}{8\times 59}\\
&=&\frac{\color{black}{\fbox{　27　}}}{\color{black}{\fbox{　59　}}}
\end{eqnarray}\)

今さらですが、割り算は逆数の掛け算です。

同様に、
　\(\begin{eqnarray}\displaystyle
P_W(B)&=&\frac{\color{blue}{P(B\cap W)}}{\color{magenta}{P(W)}}\\
&=&\frac{\frac{1}{2}\times \frac{4}{9}}{\frac{1}{2}\times \frac{59}{72}}\\
&=&\frac{4}{9}\times \frac{72}{59}\\
&=&\frac{\color{black}{\fbox{　32　}}}{\color{black}{\fbox{　59　}}}
\end{eqnarray}\)

３回中１回当たったということは起こったことなので、
　\(\,P_W(A)+P_W(B)=1\,\)
であることから\(\,P_W(A)\,\)が求まれば、
　\(\begin{eqnarray}\displaystyle
P_W(B)&=&1-P_W(A)\\
&=&1-\frac{27}{59}\\
&=&\frac{32}{59}
\end{eqnarray}\)
としても良いですが、
条件付き確率の余事象はあまり使ったことないでしょう。
（この問題ではしつこいくらいに聞いてきています。）

(2)(1)で求めた条件付き確率\(\,P_W(A)\,\)と\(\,P_W(B)\,\)において、
成り立つ事実(\(\,\mathrm{＊}\,\))について聞かれています。

　\(\begin{eqnarray}\displaystyle
P_W(A)&=&\frac{P(A\cap W)}{P(W)}\\
&=&\frac{27}{59}
\end{eqnarray}\)

　\(\begin{eqnarray}
P_W(B)&=&\frac{P(B\cap W)}{P(W)}\\
&=&\frac{32}{59}
\end{eqnarray}\)

この２つの値の関係は、
　\(\,①\,\)箱\(\,\mathrm{A}\,\)において３回中１回当たりを引く確率
　\(\,②\,\)箱\(\,\mathrm{B}\,\)において３回中１回当たりを引く確率
の関係と何が等しいか、です。

　\(\,①\,\)の確率は\(\,\displaystyle \frac{3}{8}\)
　\(\,②\,\)の確率は\(\,\displaystyle \frac{4}{9}\)

\(\color{black}{\fbox{　ス　}}\)には同じ言葉が入るので選択肢にある５つの計算をして確かめても良いですが、
条件付き確率を求めるときの計算過程を見ればその必要はありません。

(3)にその理由が書いてあるので後で気がつきます。

\(\,P_W(A)\,\)と\(\,P_W(B)\,\)は分母が同じで、
分子だけが違います。

分子である\(\,P(A\cap W)\,,\,P(B\cap W)\,\)は
　\(\displaystyle \,P(A\cap W)=\frac{1}{2}\times \frac{3}{8}\,\)
　\(\displaystyle \,P(B\cap W)=\frac{1}{2}\times \frac{4}{9}\,\)
なので、
　\(\begin{eqnarray}\displaystyle
\frac{P(A\cap W)}{P(B\cap W)}&=&\frac{\frac{3}{8}}{\frac{4}{9}}
\end{eqnarray}\)

これは\(\,P(A\cap W)\,\)と\(\,P(B\cap W)\,\)の比が、
\(\,①\,\)の確率と\(\,②\,\)の確率の比に等しいことを示しています。

比の値はどちらも
　\(\hspace{10pt}\displaystyle \frac{3}{8}\div \frac{4}{9}\\
\displaystyle =\frac{3}{8}\times \frac{9}{4}\\
\displaystyle =\frac{27}{32}\)
となるので比は同じです。

答え　\(\color{black}{\fbox{　ス　}}\)　\(\,\underline{　③　}\,\)

『比の値』って何？という中学数学を忘れている人は、
もう一度復習しておきましょう。

⇒　比例式(分数,小数,(かっこ)のついた問題)の解き方

ご安心ください。当会の中学数学サイトです。

(3)箱が３つになっても条件付き確率の比は、
それぞれの箱から３回中１回あたる確率の比と同じ、
になりそうだという会話があります。

それを確認する箱\(\,\mathrm{C}\,\)が出てきます。

箱\(\,\mathrm{C}\,\)から当たりを引く確率は\(\displaystyle \,\frac{1}{4}\,\)なので、
箱\(\,\mathrm{C}\,\)において３回中１回当たりを引く確率は
　\(\hspace{10pt}\displaystyle _3\mathrm{C}_1\times \left(\frac{1}{4}\right)^1\times \left(\frac{3}{4}\right)^2\\
\displaystyle =3\times \frac{1}{4}\times \frac{9}{16}\\
\displaystyle =\frac{27}{64}\)

３つの箱からどの箱を選ぶかは確率が等しいので、
　\(\hspace{10pt}\displaystyle P(C\cap W)=\frac{1}{3}\times \frac{27}{64}\)

(1)の\(\,①\,\)と\(\,②\,\)から
　\(\hspace{10pt}\displaystyle P(A\cap W)=\frac{1}{3}\times \frac{3}{8}\)
　\(\hspace{10pt}\displaystyle P(B\cap W)=\frac{1}{3}\times \frac{4}{9}\)
このとき、
　\(\begin{eqnarray}\displaystyle
P(W)&=&P(A\cap W)+P(B\cap W)+P(C\cap W)\\
&=&\frac{1}{3}\times \left(\color{red}{\frac{3}{8}}+\frac{4}{9}+\color{red}{\frac{27}{64}}\right)\\
&=&\frac{1}{3}\times \left(\color{red}{\frac{3\times 8+27}{64}}+\frac{4}{9}\right)\\
&=&\frac{1}{3}\times \left(\frac{51}{64}+\frac{4}{9}\right)\\
&=&\frac{1}{3}\times \frac{51\times 9+4\times 64}{64\times 9}\\
&=&\frac{1}{3}\times \frac{715}{64\times 9}
\end{eqnarray}\)

よって、
３回中１回当たったとき、選んだ箱が\(\,\mathrm{A}\,\)である条件付き確率は、
　\(\begin{eqnarray}\displaystyle
P_W(A)&=&\frac{P(A\cap W)}{P(W)}\\
&=&\frac{3}{8}\times \frac{64\times 9}{715}\\
&=&\frac{3\times 8\times 9}{715}\\
&=&\frac{\color{black}{\fbox{　216　}}}{\color{black}{\fbox{　715　}}}
\end{eqnarray}\)

途中の計算は好きにしていいです。
足し算は仕方ないとして、
掛け算部分は約分できることに期待して計算していません。笑

(4)やっと、条件付き確率を計算しなくても、
条件付き確率の大きさの比較にそれぞれの確率の比が利用できる状態になりました。

計算途中で見ておくと
　\(\hspace{10pt}\displaystyle P_W(A)=\frac{3}{8}\times \frac{64\times 9}{715}\)
　\(\hspace{10pt}\displaystyle P_W(B)=\frac{4}{9}\times \frac{64\times 9}{715}\)
　\(\hspace{10pt}\displaystyle P_W(C)=\frac{27}{64}\times \frac{64\times 9}{715}\)
となっているので条件付き確率の比と、
それぞれの確率の比が同じだとわかります。

箱が４つに増えます。
　『条件付き確率を用いて』
と問題にありますが、計算しなくて良いということですよ。

ただし、箱\(\,\mathrm{D}\,\)の確率計算はしなくてはなりません。

箱\(\,\mathrm{D}\,\)で当たりを引く確率は\(\displaystyle \,\frac{1}{5}\,\)なので、
箱\(\,\mathrm{D}\,\)において３回中１回当たりを引く確率は
　　\(\hspace{10pt}\displaystyle _3\mathrm{C}_1\times \left(\frac{1}{5}\right)\times \left(\frac{4}{5}\right)^2\\
\displaystyle =\frac{48}{125}\)

箱の違いによる確率はそれぞれ、
　\(\hspace{4pt}\displaystyle \mathrm{A：\frac{3}{8}}=0.375\,\)
　\(\hspace{4pt}\displaystyle \mathrm{B：\frac{4}{9}}=0.444\cdots\,\)
　\(\hspace{4pt}\displaystyle \mathrm{C：\frac{27}{64}}=0.421\cdots\,\)
　\(\hspace{4pt}\displaystyle \mathrm{D：\frac{48}{125}}=0.384\,\)

このことから３回中１回当たったとき、
どの箱からくじを引いた可能性が高いかは
　\(\hspace{4pt}\mathrm{B\,＞\,C\,＞\,D\,＞\,A}\)
となります。

答え　\(\color{black}{\fbox{　ト　}}\)　\(\,\underline{　⑧　}\,\)　

確率の違いを割り算で小数比較しましたが、
分母を統一して、分子の比較でも良いですよ。

もちろん比で比較して良いので、
分母の最小公倍数\(\,72000\,\)の倍数をかけて整数比較で良いです。

最小公倍数を求めるのもめんどうなので、
全部に\(\,8\times 9\times 64\times 125\,\)をかけた方が早い気もします。笑

第４問（選択問題）

第４問は整数の問題です。

不定方程式が出てきますが、
高校入試でもおなじみの問題なので作業すれば答えは出てきます。

点は円周上に\(\,\mathrm{P_0}\,\)から\(\,\mathrm{P_{14}}\,\)までの１５個あり、
さいころの出目によって石の動きが逆になるので確認しておきましょう。

サイコロの出目が、
　偶数なら反時計回りに\(\,\color{red}{5}\,\)
　奇数なら時計回りに\(\,\color{blue}{3}\,\)
石を移動させます。

方向を1つに見れば
　偶数なら反時計回りに\(\,\color{red}{+5}\,\)
　奇数なら反時計回りに\(\,\color{blue}{-3}\,\)
移動させることになります。

問題を解き進めれば分かりますが、
反時計回りに移動する数が
　\(\,0\,,\,15\,,\,-15\,\)
などは同じ位置を示します。
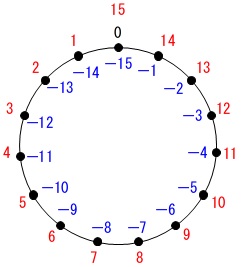(1)さいころを５回投げます。

　「\(\,\mathrm{P_0}\,\)にあった石が\(\,\mathrm{P_1}\,\)に移動する。」

このとき、偶数と奇数は何回出たかが問題です。

　偶数が\(\,x\,\)回
出たとすると
　奇数は\(\,5-x\,\)回
出たことになるので、
　\(\begin{eqnarray}\displaystyle
\color{red}{5}x+(\color{blue}{-3})(5-x)&=&+1\\
5x-15+3x&=&1\\
8x&=&16\\
x&=&\color{black}{\fbox{　2　}}
\end{eqnarray}\)

これは５回中偶数の目が出た回数で、
奇数の目が出た回数は\(\color{black}{\fbox{　3　}}\)回です。

他にも不定方程式
　\(\,5x-3y=1\,\)
を満たす整数解はありますが、

　\(\begin{array}{|c|c|c|c|} \hline
x & y & 5x-3y & 石の位置\\ \hline
0 & 5 & -15 & \mathrm{P_0}\\ \hline
1 & 4 & -7 & \mathrm{P_8}\\ \hline
2 & 3 & 1 & \mathrm{P_1}\\ \hline
3 & 2 & 9 & \mathrm{P_9}\\ \hline
4 & 1 & 17 & \mathrm{P_2}\\ \hline
5 & 0 & 25 & \mathrm{P_{10}}\\ \hline
\end{array}\)

５回までの中では他にありません。

(2)不定方程式を解きます。

　\(5x-3y=8　･･･①\)

(1)から
　\(\,5\times 2-3\times 3=1\,\)
なので両辺\(\,8\,\)倍して
　\(5(2\times 8)-3(3\times 8)=8　･･･②\)

\(\,①-②\,\)から右辺が\(\,0\,\)になることを利用して、
　\(\begin{eqnarray}
5x-5(2\times 8)&=&3y-3(3\times 8)\\
5(x-2\times 8)&=&3(y-3\times 8)
\end{eqnarray}\)

これは左辺は\(\,3\,\)の倍数で、右辺が\(\,5\,\)の倍数であることを意味しています。

\(\,5\,\)と\(\,3\,\)が互いに素だから、
（かっこ）の中が\(\,3\,\)の倍数と\(\,5\,\)の倍数になります。

整数\(\,k\,\)を用いて
　\(\begin{eqnarray}
x-2\times 8&=&3k\\
x&=&2\times 8+\color{black}{\fbox{　3　}}k
\end{eqnarray}\)
および
　\(\begin{eqnarray}
y-3\times 8&=&5k\\
y&=&3\times 8+\color{black}{\fbox{　5　}}k
\end{eqnarray}\)

ここで\(\,0≦y＜5\,\)を満たすのは、
　\(\hspace{10pt}
0≦3\times 8+5k＜5\\
-24≦5k＜-19\\
-4.8≦k＜-3.8\)

から\(\,k=-4\,\)のときで、
　\(\hspace{10pt}x=\color{black}{\fbox{　4　}}\,,\,y=\color{black}{\fbox{　4　}}\)

これはさいころを\(\,\color{black}{\fbox{　8　}}\,\)回投げて、
　偶数の目が\(\,4\,\)回、
　奇数の目が\(\,4\,\)回、
出れば\(\,\mathrm{P_0}\,\)の石が\(\,\mathrm{P_8}\,\)に移動するということです。

(3)偶数の目が\(\,1\,\)回出ると\(\,+5\,\)移動することから、
偶数の目が\(\,3\,\)回出ると\(\,+15\,\)で１周するので、
(2)の場合の偶数の目が\(\,4\,\)回より\(\,3\,\)回少ない
　偶数の出た目が\(\,\color{black}{\fbox{　1　}}\,\)回
　奇数の出た目が\(\,\color{black}{\fbox{　4　}}\,\)回
のさいころを\(\,\color{black}{\fbox{　5　}}\,\)回投げる場合でも\(\,\mathrm{P_0}\,\)の石が\(\,\mathrm{P_8}\,\)に移動します。

これは問題の\(\,(*)\,\)に書いてあるので簡単に済ませておきます。

(4)(3)の\(\,(*)\,\)で『\(\,15\,\)個先に移動すれば元の点に戻る。』
ということから、
　偶数\(\,3\,\)回で\(\,+15\,\)移動する。
　奇数\(\,5\,\)回で\(\,-15\,\)移動する。
ので
　偶数\(\,3\,\)回
　奇数\(\,5\,\)回
より少ない回数の組み合わせで移動先が決まるということがわかります。

偶数、奇数のどちらかが出ないということもあるので、
　偶数は\(\,0\,,\,1\,,\,2\,\)回
　奇数は\(\,0\,,\,1\,,\,2\,,\,3\,,\,4\,\)回
の組み合わせだけです。
（偶数\(\,0\,\)、奇数\(\,0\,\)はさいころを振っていない。）

すべて書き出すと移動先は
　\(\begin{array}{|c|c|c|c|} \hline
偶数\,x\, & 奇数\,y\, & 5x-3y & 移動先 & 回数 \\ \hline
0 & 1 & -3 & \color{red}{\mathrm{P_{12}}} & 1\\ \hline
0 & 2 & -6 & \mathrm{P_9} & 2\\ \hline
0 & 3 & -9 & \mathrm{P_6} & 3\\ \hline
0 & 4 & -12 & \mathrm{P_3} & 4\\ \hline
1 & 0 & +5 & \mathrm{P_{5}} & 1\\ \hline
1 & 1 & +2 & \mathrm{P_2} & 2\\ \hline
1 & 2 & -1 & \color{red}{\mathrm{P_{14}}} & 3\\ \hline
1 & 3 & -4 & \color{red}{\mathrm{P_{11}}} & 4\\ \hline
1 & 4 & -7 & \mathrm{P_{8}} & 5\\ \hline
2 & 0 & +10 & \color{red}{\mathrm{P_{10}}} & 2\\ \hline
2 & 1 & +7 & \mathrm{P_7} & 3\\ \hline
2 & 2 & +4 & \mathrm{P_{4}} & 4\\ \hline
2 & 3 & +1 & \mathrm{P_{1}} & 5\\ \hline
2 & 4 & -2 & \color{red}{\mathrm{P_{13}}} & 6\\ \hline
\end{array}\)

問題は\(\,5\,\)点についての最小回数なので、
５つの不定方程式を解いて調べれても良いです。
が、そちらはお任せしますので(2)のやり方でやってみてください。

例えば\(\,5x-3y=\color{red}{13}\,\)のとき、
　\(x=2\times \color{red}{13}+3k\)
　\(y=3\times \color{red}{13}+5k\)
から、\(\,k=-7\,\)のとき
　\(\,x=5\,,\,y=4\,\)
となり\(\,9\,\)回ですが、\(\,x\,\)は\(\,3\,\)回で元に戻るので、
　\(\,x=2\,,\,y=4\,\)
の\(\,6\,\)回の方が少ない回数で\(\,\mathrm{P_{13}}\,\)に移動できます。　

答え
　\(\color{black}{\fbox{　サ　}}\)　\(\,\underline{　③　}\,\)　\(\color{black}{\fbox{　シ　}}\)　\(\color{black}{\fbox{　6　}}\)回

第５問（選択問題）

第５問は幾何になります。

選択問題の中で一番日本語が少なく、
シンプルに見える数学らしい問題ですが、
シンプルな問題ほど難しくなるのも数学です。笑

ただ、誘導がはっきりされているので難しくはありません。

『\(\,\mathrm{△ABC}\,\)において
　\(\,\mathrm{AB=3}\,\)
　\(\,\mathrm{BC=4}\,\)
　\(\,\mathrm{AC=5}\,\)
とする。』
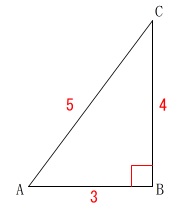\(\,\mathrm{△ABC}\,\)は直角三角形です。

『\(\,\mathrm{∠BAC}\,\)の二等分線と辺\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{D}\,\)とする。』
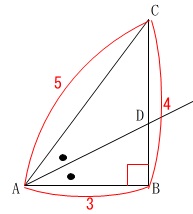角の二等分線定理から、
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:AC}&=&\mathrm{BD:DC}\\
3:5&=&\mathrm{BD:DC}
\end{eqnarray}\)

\(\,\mathrm{BC=4}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{BD}&=&\frac{3}{3+5}\times 4\\
&=&\frac{\color{black}{\fbox{　3　}}}{\color{black}{\fbox{　2　}}}
\end{eqnarray}\)

\(\,\mathrm{AD}\,\)の長さは、
三平方の定理が使えます。
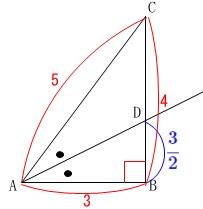\(\,\mathrm{△ABD}\,\)は直角三角形なので
　\(\begin{eqnarray}\mathrm{AD^2}&=&\mathrm{AB^2+BD^2}\\
&=&3^2+\left(\frac{3}{2}\right)^2\\
&=&9+\frac{9}{4}\\
&=&\frac{45}{4}\end{eqnarray}\)

\(\,\mathrm{AD\,＞\,0}\,\)より
　\(\hspace{10pt}\displaystyle \mathrm{AD}=\frac{\color{black}{\fbox{　3　}}\sqrt{\color{black}{\fbox{　5　}}}}{\color{black}{\fbox{　2　}}}\)

『\(\,\mathrm{∠BAC}\,\)の二等分線と\(\,\mathrm{△ABC}\,\)の外接円\(\,\mathrm{O}\,\)との交点で
点\(\,\mathrm{A}\,\)とは異なる点を\(\,\mathrm{E}\,\)とする。』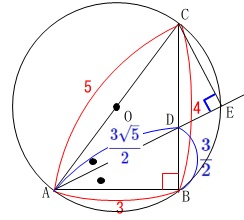
『\(\,\mathrm{△AEC}\,\)に着目すると』、
\(\,\mathrm{∠ABC=90^{\circ}}\,\)であることから\(\,\mathrm{AC}\,\)は円\(\,\mathrm{O}\,\)の直径です。

このとき\(\,\mathrm{△AEC}\,\)も直角三角形になります。

\(\displaystyle \,\mathrm{BD=\frac{3}{2}}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{DC}&=&\mathrm{BC-BD}\\
&=&4-\frac{3}{2}\\
&=&\color{blue}{\frac{5}{2}}\end{eqnarray}\)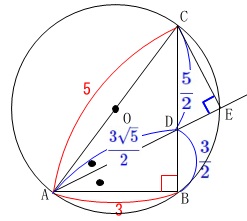この問題の、
　『\(\,\mathrm{△AEC}\,\)に着目すると』
は、\(\,\mathrm{∠AEC}\,\)が\(\,90°\,\)であることをいっているのか、
\(\,\mathrm{△AEC}\,\)を利用して進めるように言っているのかわかりにくいです。

\(\,\mathrm{∠AEC=90^{\circ}}\,\)であることまでを言っているなら
　\(\,\mathrm{△ABD}\,\)　∽　\(\,\mathrm{△CED}\,\)
の利用を考えただろうし、
　\(\,\mathrm{△AEC}\,\)が直角三角形
ということだけで、
\(\,\mathrm{△AEC}\,\)に三平方の定理の利用を考えたかもしれません。

\(\,\mathrm{AE}\,\)を求めるだけなのでどちらでも構いません。

相似利用の場合

　\(\,\mathrm{△ABD}\,\)　∽　\(\,\mathrm{△CED}\,\)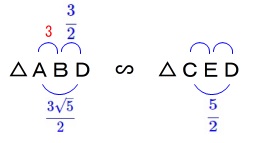
を利用すると、
　\(\begin{eqnarray}\displaystyle
\mathrm{BD:DA}&=&\mathrm{ED:DC}\\
\frac{3}{2}:\frac{3\sqrt{5}}{2}&=&\mathrm{ED}:\frac{5}{2}\\
3:3\sqrt{5}&=&2\,\mathrm{ED}:5\\
2\times 3\sqrt{5}\,\mathrm{ED}&=&3\times 5\\
\mathrm{ED}&=&\frac{3\times 5}{2\times 3\sqrt{5}}\\
&=&\frac{\sqrt{5}}{2}
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{AE}&=&\mathrm{AD+ED}\\
&=&\frac{3\sqrt{5}}{2}+\frac{\sqrt{5}}{2}\\
&=&\color{black}{\fbox{　2　}}\sqrt{\color{black}{\fbox{　5　}}}
\end{eqnarray}\)

三平方の定理利用の場合

\(\,\mathrm{△AEC}\,\)と\(\,\mathrm{△CED}\,\)は直角三角形で\(\,\mathrm{CE}\,\)が共通になっています。
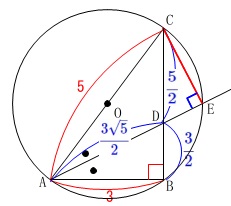\(\,\mathrm{△AEC}\,\)において
　\(\hspace{10pt}\mathrm{CE^2=AC^2-AE^2}\)
\(\,\mathrm{△CED}\,\)において
　\(\hspace{10pt}\mathrm{CE^2=DC^2-DE^2}\)

\(\,\mathrm{AE}=x\,\)とおくと\(\displaystyle \,\mathrm{DE}=x-\frac{3\sqrt{5}}{2}\,\)とおけるので、
上の関係式において左辺が\(\,\mathrm{CE^2}\,\)で同じなので、
右辺が等しくなることから
　\(\begin{eqnarray}\displaystyle
\mathrm{AC^2-AE^2}&=&\mathrm{DC^2-DE^2}\\
5^2-x^2&=&\left(\frac{5}{2}\right)^2-\left(x-\frac{3\sqrt{5}}{2}\right)^2
\end{eqnarray}\)
（途中の計算を省略するので自分で処理しておいてください。）
　\(\begin{eqnarray}\displaystyle
3\sqrt{5}x&=&30\\
x&=&\frac{10}{\sqrt{5}}\\
&=&\color{black}{\fbox{　2　}}\sqrt{\color{black}{\fbox{　5　}}}
\end{eqnarray}\)

どちらで求めても大した差ではありません。

次です。
　\(\,\mathrm{AB\,,\,AC}\,\)の両方に接し、
　外接円\(\,\mathrm{O}\,\)に接する円の中心を\(\,\mathrm{P}\,\)
　円\(\,\mathrm{P}\,\)の半径を\(\,r\,\)
　外接円\(\,\mathrm{O}\,\)と円\(\,\mathrm{P}\,\)の接点を\(\,\mathrm{F}\,\)
　直線\(\,\mathrm{PF}\,\)と外接円\(\,\mathrm{O}\,\)との接点\(\,\mathrm{F}\,\)とは異なる点を\(\,\mathrm{G}\,\)
とする。位置関係の整理が必要です。
　円\(\,\mathrm{P}\,\)の中心は\(\,\mathrm{∠BAC}\,\)の二等分線上にあり、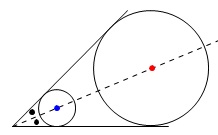
点\(\,\mathrm{F}\,\)は円\(\,\mathrm{O}\,\)の円\(\,\mathrm{P}\,\)の接点なので、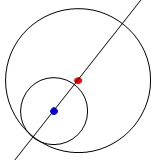
　点\(\,\mathrm{F\,,\,P\,,\,O\,,\,G}\,\)は一直線上にあります。
円\(\,\mathrm{O}\,\)の半径なので
　\(\displaystyle \mathrm{AO}=\color{red}{\frac{5}{2}}\)

また、
　\(\,\mathrm{△APO}\,\)　∽　\(\,\mathrm{△ADB}\,\)
であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{AO:OP}&=&\mathrm{AB:BD}\\
\frac{5}{2}:r&=&3:\frac{3}{2}\\
3r&=&\frac{5}{2}\times \frac{3}{2}\\
r&=&\frac{\color{black}{\fbox{　5　}}}{\color{black}{\fbox{　4　}}}
\end{eqnarray}\)

とすると誘導に乗れていませんでした。
元に戻ります。（面倒くさい）

点\(\,\mathrm{P}\,\)から辺\(\,\mathrm{AB}\,\)に垂線を下ろし\(\,\mathrm{AB}\,\)との交点を\(\,\mathrm{H}\,\)とすると、
\(\,\mathrm{PH}\,\)は円\(\,\mathrm{P}\,\)の半径\(\,r\,\)であり、
　\(\,\mathrm{△ABD}\,\)　∽　\(\,\mathrm{△AHP}\,\)
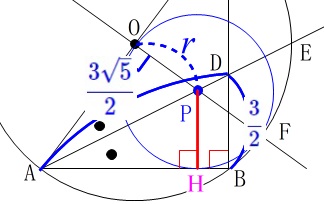このことから
　\(\begin{eqnarray}\displaystyle
\mathrm{AD:BD}&=&\mathrm{AP:HP}\\
\frac{3\sqrt{5}}{2}:\frac{3}{2}&=&\mathrm{AP}:r\\
3\,\mathrm{AP}&=&3\sqrt{5}\,r\\
\mathrm{AP}&=&\sqrt{\color{black}{\fbox{　5　}}}\,r
\end{eqnarray}\)

\(\,\mathrm{PG}\,\)は直径である線分\(\,\mathrm{FG}\,\)から半径である\(\,\mathrm{PF}\,\)を引けば出ます。

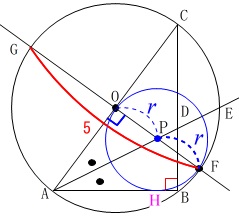
　\(\begin{eqnarray}\displaystyle
\mathrm{PG}&=&\mathrm{FG-PF}\\
&=&\color{black}{\fbox{　5　}}-r
\end{eqnarray}\)

どうしても使って欲しかったのでしょう。

　『方べきの定理により』

　\(\begin{eqnarray}\displaystyle
\mathrm{PE}&=&\mathrm{AE-AP}\\
&=&2\sqrt{5}-\sqrt{5}\,r\\
&=&\color{magenta}{\sqrt{5}(2-r)}
\end{eqnarray}\)
であることから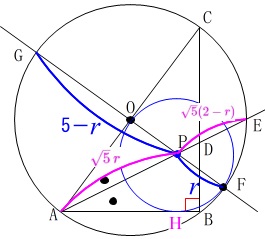
　\(\begin{eqnarray}\displaystyle
\mathrm{AP}\times \mathrm{PE}&=&\mathrm{PG}\times \mathrm{FP}\\
\sqrt{5}\,r\times \sqrt{5}(2-r)&=&(5-r)\times r\\
5\,r(2-r)&=&5\,r-r^2\\
4r^2-5r&=&0\\
r\,(4r-5)&=&0
\end{eqnarray}\)

\(\,r≠0\,\)なので
　\(\hspace{10pt}\displaystyle r=\frac{\color{black}{\fbox{　5　}}}{\color{black}{\fbox{　4　}}}\)

\(\,\mathrm{△ABC}\,\)の内心は直角三角形の内心なので正方形ができます。
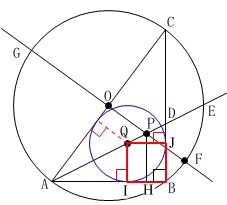この正方形の１辺は内接円の半径でもあるので、
\(\,\mathrm{△ABC}\,\)の内接円の半径を\(\,a\,\)として、
面積の公式を利用して内接円の半径を求めます。
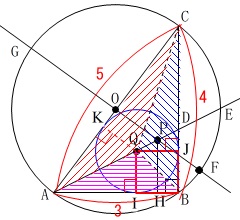\(\,\mathrm{△ABC}\,\)の面積は底辺\(\,3\,\)、高さ\(\,4\,\)の三角形なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\mathrm{△QAB+△QBC+△QAC}\\
\frac{1}{2}\times 3\times 4&=&\frac{a(3+4+5)}{2}\\
a&=&\color{black}{\fbox{　1　}}
\end{eqnarray}\)

または、
合同な三角形３つができることから、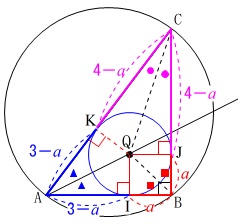\(\,\mathrm{BJ=BI}=a\,\)とすると、
　\(\hspace{10pt}\mathrm{CJ=CK}=\color{magenta}{4-a}\)
　\(\hspace{10pt}\mathrm{AI=AK}=\color{blue}{3-a}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AC}&=&\mathrm{AK+CK}\\
5&=&(3-a)+(4-a)\\
a&=&\color{black}{\fbox{　1　}}
\end{eqnarray}\)

大した差はないので思い立った方法で進めた方が早いです。

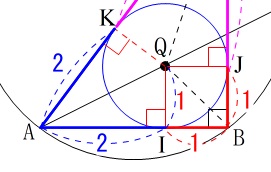このとき\(\,\mathrm{△AQI}\,\)から
　\(\begin{eqnarray}\displaystyle
\mathrm{AQ^2}&=&\mathrm{AI^2+QI^2}\\
&=&1^2+2^2\\
&=&5\\
\mathrm{AQ}&=&\sqrt{\color{black}{\fbox{　5　}}}　(＞0)
\end{eqnarray}\)

また、円\(\,\mathrm{P}\,\)と辺\(\,\mathrm{AB}\,\)との接点を\(\,\mathrm{H}\,\)とすると、
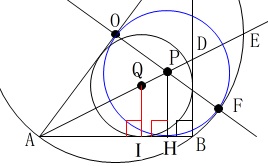\(\,\mathrm{△AQI}\,\)　∽　\(\,\mathrm{△APH}\,\)　なので、
　\(\hspace{10pt}\mathrm{AQ}=\sqrt{5}\)
　\(\hspace{10pt}\displaystyle \mathrm{AP}=\frac{5\sqrt{5}}{4}\)
　\(\hspace{10pt}\mathrm{AI}=2\)
であることから（今までに求めてあります。）
　\(\begin{eqnarray}\displaystyle
\mathrm{AQ:AP}&=&\mathrm{AI:AH}\\
\sqrt{5}:\frac{5\sqrt{5}}{4}&=&2:\mathrm{AH}\\
\mathrm{AH}&=&\frac{\color{black}{\fbox{　5　}}}{\color{black}{\fbox{　2　}}}
\end{eqnarray}\)

『以上から』という問題の言葉は、
\(\,\mathrm{AH}\,\)まで長さを求めていることから、
「方べきの定理」を利用して、ということでしょうか。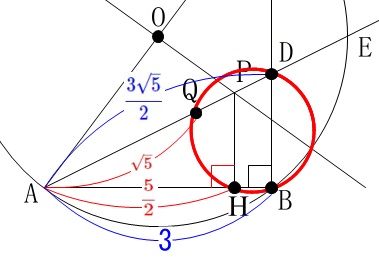点\(\,\mathrm{H\,,\,B\,,\,D\,,\,Q}\,\)において、
方べきの定理
　\(\hspace{10pt}\mathrm{AQ\times AD=AH\times AB}\)
が成り立てば４点は同じ円周上にあると言えます。
　\(\hspace{10pt}\displaystyle \mathrm{AQ\times AD}\\
\displaystyle =\sqrt{5}\times \frac{3\sqrt{5}}{2}\\
\displaystyle =\frac{15}{2}\)

　\(\hspace{10pt}\displaystyle \mathrm{AH\times AB}\\
\displaystyle =\frac{5}{2}\times 3\\
\displaystyle =\frac{15}{2}\)

\(\,(\mathrm{a})\,\)は正しい。

また、異なる３点を通る円は１つしかないので、
　\(\,\mathrm{H\,,\,B\,,\,Q}\,\)
を通る円は１つしかありません。

だから\(\,\mathrm{H\,,\,B\,,\,E\,,\,Q}\,\)は同一円周上にはありません。

\(\,\mathrm{(b)}\,\)は誤り。

答え　\(\color{black}{\fbox{　タ　}}\)　\(\,\underline{　①　}\,\)

四角形\(\,\mathrm{HBDQ}\,\)について、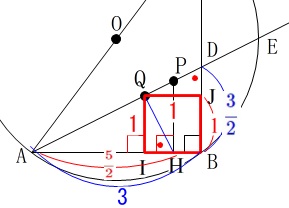
ここまで出てきた長さと正方形\(\,\mathrm{IBJQ}\,\)から
　\(\,\mathrm{△HQI　≡　△DQJ}\,\)
であることから
　\(\,\mathrm{∠QHI=∠QDJ}\,\)
および
　\(\,\mathrm{∠HBD=∠HQD=90^{\circ}}\,\)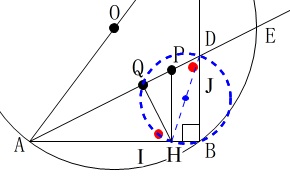
なので\(\,\mathrm{HD}\,\)を直径とする円に内接していることが、
方べきの定理でなくても示せます。