ベクトルの問題を考えるときは必ず図形が関係してきますよね。
ベクトルの問題と考えベクトルの線型性だけで考えるのか、
幾何の定理は使えないのか悩むことがありませんか？
どちらでも答えが引き出せるように利用法をここで復習しておきましょう。
ベクトル問題は図を書くことから
空間ベクトルの問題では座標が、
平面ベクトルの問題は三角形や円が良く出てきます。
ここでは平面の問題を例としてあげてみます。
また、線分\(\,\mathrm{ＡＰ}\,\)の延長が\(\,\mathrm{ＢＣ}\,\)と交わる点をＱとする。
このとき、\(\overrightarrow{\mathrm{AP}}\) を \( \overrightarrow{\mathrm{AB}} , \overrightarrow{\mathrm{AC}}\) で表せ。
また、ＡＰ：ＰＱ を求めよ。
過去記事を見てくれている人はわかっていると思いますが、
最初にすることは、『図を書くこと』です。
できるだけの情報を図示しましょう。
図示の要領は、問題文の順序通りで良いのです。
ちょっと違うと、途中で気がついてもそのままいけそうなら行けばいい。
しかし、あまりにも違いすぎると分かれば修正するか、
書き直すかのどちらかした方がいいです。
終盤になって書き直すには時間がかかりますが、
図なしや検討もつかない図よりは断然早いですからね。
三角比、平面幾何、ベクトルにおいて図はそれくらい重要なんです。
（他はグラフ等）
問題の順序通りに図示してみましょう。
「△ＡＢＣにおいて，」
この段階ではどのような三角形かは分かりません。
後を読むと、「内分」「内分」と続くので、
△の内部で納まる可能性が高いので、
△ＡＢＣを大きめにします。
辺ＡＢを３：２に内分する点をＤ ⇒
辺ＡＣを２：１に内分する点をＥ ⇒
線分ＢＥ，ＣＤの交点をＰ ⇒
線分ＡＰの延長が辺ＢＣと交わる点をＱ ⇒
これらを図示すると、下図のようになります。
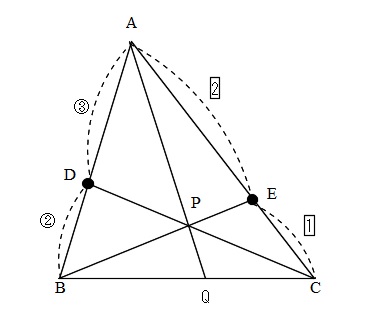
試験場ではフリーハンドになるからだいたいで良いですよ。
始点を1つに固定する
「始点は１つに」が基本ですが、
問題に \(\overrightarrow{\mathrm{AB}} , \overrightarrow{\mathrm{AC}}\) で表せと指示があるので、
始点はＡで決まりです。
２つの独立なベクトルも、
\(\overrightarrow{\mathrm{AB}} = \vec{b} ，\overrightarrow{\mathrm{AC}} = \vec{c}\)
とおいて続けましょう。
（この２つで平面上すべてのベクトルが表せるんです。）
\(\overrightarrow{\mathrm{AP}}\) を \( \vec{b} , \vec{c}\) で表すのに必要な線分比ですが、
２つの方法があります。
１つは、幾何の性質を利用し線分の比を出しておくこと。
もう一つは、ベクトルの線型性を利用して線分の比を出すこと。
どちらでもいいけど、
両方できないとセンターのような誘導方式には対応できませんので、
方針だけでも簡単に両方示しておきます。
幾何の定理を使ったベクトル表示
１つは簡単です。
メネラウスの定理を使って、線分比をだす方法です。
\(\displaystyle \mathrm{\frac{AD}{DB}} \times \mathrm{\frac{BP}{PE}} \times \mathrm{\frac{EC}{CA}} = 1 \)
⇔ \(\displaystyle \frac{3}{2} \times \mathrm{\frac{BP}{PE}} \times \frac{1}{3} = 1\)
⇔ \(\,\mathrm{BP：PE=2：1}\,\)
ＤＰ：ＰＣも同様に出せます。
またチェバの定理から
\(\displaystyle \mathrm{\frac{AD}{DB} \times \frac{BQ}{QC} \times \frac{CE}{EA}} = 1 \)
⇔ \(\displaystyle \frac{3}{2} \times \mathrm{\frac{BQ}{QC}} \times \frac{1}{2} = 1\)
⇔ \(\,\mathrm{BQ:QC=4:3}\,\)
後半はこれを使ってすぐに求まります。
これらの線分比と内分点の公式から
\(\begin{eqnarray}\displaystyle
\overrightarrow{\mathrm{AP}} &=& \frac{\vec{b} + 2 \times \frac{2}{3} \vec{c}}{2+1} \\
&=& \frac{1}{3}\vec{b} + \frac{4}{9}\vec{c}\end{eqnarray}\)
つまり、
\(\hspace{10pt}\displaystyle \overrightarrow{\mathrm{AP}} &=& \frac{1}{3}\overrightarrow{\mathrm{AB}} + \frac{4}{9}\overrightarrow{\mathrm{AC}}\)
\(\,\mathrm{DP:PC}\,\) や \(\,\mathrm{AP：PQ}\,\)
これらもメネラウスの定理で出しておくと、
センターでは面積比まで聞いてくるので重宝します。
\(\,\mathrm{AP：PQ}\,\)はこの問題の後半で問われています。
まとめ
線型結合と線型性を利用して解く方法も次に示しますが、ここで一度まとめておきました。
ベクトルの問題とすぐにわかる問題でも、幾何の知識は使って良いんです。
センター（共通テストやセンター試験）のような誘導タイプだと、
途中が埋められないということはあるかもしれませんが結果は同じです。
線型性を理解しながら利用出来るとベクトルは強いです。
結果がわかれば途中も埋められるようになりますので、
引き出しを多くするという意味からも幾何の復習もしっかりやっておきましょう。
慣れてしまえばベクトルはものすごく便利な道具になりますよ。