平面ベクトルの内分点外分点の利用と3点が一直線上にある証明　

ベクトルの平面図形における内分点、外分点への利用方法をお伝えします。
最近では共通テスト（センター試験）の数学ⅡＢで、ベクトルは空間の中で扱われることが多いですが、平面での扱いが基本です。
3点が一直線上にある条件と証明も確認しておきますので参考にして下さい。

ベクトルと図形の共通点

別記事でベクトルの基本的な用語は説明してありますので、
早速ですが平面図形の例題を用いて説明します。

図は自分で書いて説明を見てください。
他人の図や式を見て自分でやった気になることが、
問題を難しく感じさせる原因でもあります。

問題集などで図形の問題を解く解きもこれをやらないと力がつきにくいです。
また、参考書や問題集を活かすことが出来ていない人は、
ここが出来ていない人がほとんどですので気をつけて見てください。

ちょっとした手間がかかりますが、
これが成績アップに大きく関係してくるのですよ。

例題

平行四辺形 \(\,\mathrm{ABCD}\,\) において，
辺 \(\,\mathrm{AB}\,\) を\(\,2：1\,\)に内分する点を \(\,\mathrm{E}\,\) ，
対角線 \(\,\mathrm{BD}\,\) を\(\,1：3\,\)に内分する点を \(\,\mathrm{F}\,\) とする。
(１)ベクトル　\(\overrightarrow{\mathrm{EF}}\)　を　\(\overrightarrow{\mathrm{AB}}　,　\overrightarrow{\mathrm{AD}}\)　で表せ。
(２) \(\,\mathrm{E ，F ，C}\,\) は同一直線上にあることを示せ。

問題に「平行四辺形」などと、
図形を日本語で書かれている場合、
問題を読み続けてもなかなか問題の意味は取れません。

何をするか？

図を書いて意味をとりながら進めるのです。

センターでも本試でも図がないのが普通なので、
「図は自分で書いて下さい。」
と図を書くことも数学の解答課程だといっているようなものです。

これは、三角比と幾何の融合分野と同じことが言えますよね。

図を書くときは、できるだけ大きく、問題の条件に忠実に書いた方が分かり易いです。

ただし、あまり書き出しを大きくすると図が紙面上で納まらないことがあるので注意が必要となる場合もありますが、基本は大きく、です。

書ききれないときは書き直すか、そのまま行くかは状況によります。
正確さもこだわる必要はありません。
時間の問題もあるのでおおよそ合えばOk.です。

では、問題に入ります。
条件を図示してみましょう。

平行四辺形 \(\,\mathrm{ABCD}\,\)　⇒
　辺\(\,\mathrm{AB}\,\) を \(\,2:1\,\) に内分する点 \(\,\mathrm{E}\,\)　⇒
　辺\(\,\mathrm{BD}\,\) を \(\,1:3\,\) に内分する点 \(\,\mathrm{F}\,\)　⇒
から

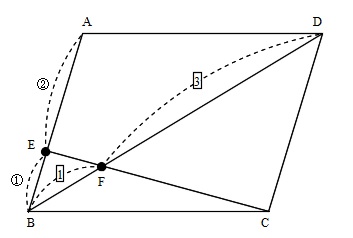
となりました。

途中までは \(\,\mathrm{F}\,\) の位置が分かりづらいですね。
(2)を見て、\(\,\mathrm{E，F，C}\,\)を一直線上、つまり \(\,\mathrm{CE}\,\) と \(\,\mathrm{BD}\,\) の交点が \(\,\mathrm{F}\,\) であるように図を作成しました。

ベクトルは始点は１つにする

それでは問題を解いて行きましょう。

(1)「ベクトル　\( \overrightarrow{\mathrm{EF}}\)　を　\( \overrightarrow{\mathrm{AB}}　， \overrightarrow{\mathrm{AD}}\)　で」とあります。

ベクトルでは、
　「始点を１つに」
そして、
　「平面では２つ」の基底となる線型独立なベクトルですべてのベクトルが表すことができる。
（「空間では３つ」となります。詳しくは別の機会に）
ということを大いに利用して下さい。

線型独立、１次独立という言葉を学校で習っていない人は、
　「平行でもなく、零でもない２つのベクトルどうしを線型独立という。」
と軽く理解しておいて下さい。
( \( \vec{a} \neq \vec{0}　,　\vec{b} \neq \vec{0}\)　,　\(\vec{a}\,∦\,\vec{b} \)（平行ではない。） )

この問題は、「 \(　\overrightarrow{\mathrm{AB}}　,　\overrightarrow{\mathrm{AD}}\) で」とすることで、
始点を \(\,\mathrm{A}\,\) に、\( \overrightarrow{\mathrm{AB}}　,　\overrightarrow{\mathrm{AD}}\)　を基底にするといいと教えてくれています。
（\( \overrightarrow{\mathrm{AB}}\,,\,\overrightarrow{\mathrm{AD}}\)だけで表すということです。）

　\( \overrightarrow{\mathrm{AB}} = \vec{b}　，　\overrightarrow{\mathrm{AD}} = \vec{d}\)　と表すことにします。
（この２つの基底ベクトルで平面上の点すべてのベクトルを表せます。)

始点は１つにすることも基本です。
　\( \overrightarrow{\mathrm{EF}}\)　の始点を \(\,\mathrm{A}\,\) に統一します。

　\( \overrightarrow{\mathrm{EF}} = \overrightarrow{\mathrm{AF}} – \overrightarrow{\mathrm{AE}} \)
（この変形は確実に出来るようになっておきましょう。）

ベクトルの内分点と外分点の公式

ベクトル　\( \vec{a}\,,\,\vec{b}\)　を　\( \color{red}{m}\, :\, \color{blue}{n} \)　に内分するベクトル　\( \vec{p}\)　は
　\(\hspace{10pt}\displaystyle \vec{p} = \frac{\color{blue}{n}\,\vec{a} + \color{red}{m}\,\vec{b}}{ \color{red}{m} + \color{blue}{n} } \)
です。これは数直線や平面座標の\(\,2\,\)点を内分する場合と同じです。

外分点を表すベクトルは、
　ベクトル　\( \vec{a}　,　\vec{b}\)　を「\(\,\color{red}{m}\,:\, (\color{blue}{-n})\,\)に内分する」
と形式的に考えれば同じように表せます。
　\(\begin{eqnarray}\displaystyle
\vec{p}&=&\frac{(\color{blue}{-n})\,\vec{a} + \color{red}{m}\,\vec{b}}{ \color{red}{m} + (\color{blue}{-n})} \\
&=&\frac{\color{blue}{-n}\,\vec{a} + \color{red}{m}\,\vec{b}}{ \color{red}{m}\,\color{blue}{-\,n}}
\end{eqnarray}\)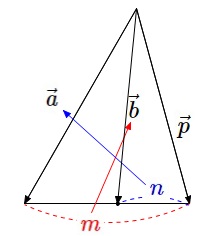このことは図形と方程式の基本事項にありますので確認しておいて下さい。

⇒　図形と方程式の要点

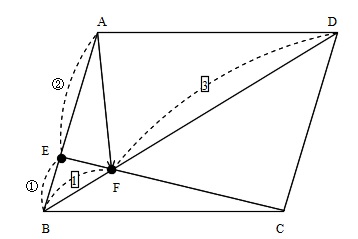
内分点の公式から　\( \overrightarrow{\mathrm{AF}}\,,\,\overrightarrow{\mathrm{AE}}\)　は
　\( \displaystyle \overrightarrow{\mathrm{AF}} = \frac{3\vec{b} + \vec{d}}{ 4 } \)
　\( \displaystyle \overrightarrow{\mathrm{AE}} = \frac{2\vec{b}}{ 3 } \)
となるので
　\(\begin{eqnarray}\displaystyle \overrightarrow{\mathrm{EF}} &=&\frac{3\,\vec{b} + \vec{d}}{4} – \frac{2\,\vec{b}}{3}\\
&=&\frac{3\,(3\,\vec{b} + \vec{d})-4\,(2\,\vec{b})}{12}\\
&=&\frac{\vec{b}+3\,\vec{d}}{12}\\
&=& \frac{\overrightarrow{\mathrm{AB}} + 3\,\overrightarrow{\mathrm{AD}}}{ 12 }　･･･①
\end{eqnarray}\)
または
　\(\displaystyle \overrightarrow{\mathrm{EF}} = \frac{1}{12} \overrightarrow{\mathrm{AB}} + \frac{1}{4} \overrightarrow{\mathrm{AD}}\)

これはどっちでも良いですが、
マークの場合、回答欄の形でかき分けます。

３点が直線上にならぶ条件と証明（復習）

（２）は以前の復習になります。
「\(\,\mathrm{ E，F，C}\,\) が一直線上」⇔「 \( \overrightarrow{\mathrm{EF}} = \color{red}{k}\,\overrightarrow{\mathrm{EC}}\) となる実数\(\,\color{red}{k}\,\)が存在する」

始点がそろっていなくても言えることですが、
始点をそろえるという基本通りに進めると良いです。

　\( \overrightarrow{\mathrm{EC}} = \overrightarrow{\mathrm{AC}} – \overrightarrow{\mathrm{AE}}\)

始点を\(\,\mathrm{A}\,\)にそろえました。

ここで
　\(\overrightarrow{\mathrm{AC}} = \vec{b} + \vec{d} \)
　\(\displaystyle \overrightarrow{\mathrm{AE}} = \frac{2\,\vec{b}}{ 3 } \)
なので
　\(\begin{eqnarray}\displaystyle \overrightarrow{\mathrm{EC}} &=& (\vec{b} + \vec{d}) – \frac{2\,\vec{b}}{ 3 } \\
&=&\frac{3\,(\vec{b} + \vec{d}-2\,\vec{b})}{3}\\
&=& \frac{\vec{b} + 3\vec{d}}{ 3 }\end{eqnarray} \)
先に①の関係式
　\(\displaystyle \overrightarrow{\mathrm{EF}} = \frac{\overrightarrow{b} + 3\,\overrightarrow{d}}{ 12 }\)
が言えていたので　
　\(\displaystyle \overrightarrow{\mathrm{EF}} = \color{blue}{\frac{1}{4}}\,\overrightarrow{\mathrm{EC}}\)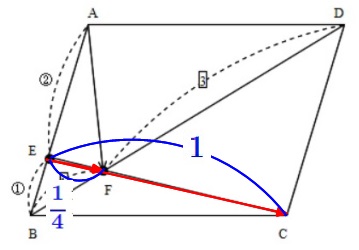よって、
　始点が同じで実数倍で表されているので\(\,\mathrm{E\,,\,C\,,\,F}\,\)は一直線上にある。
と言えます。