ベクトルの線形結合を利用した係数決定問題の解き方です。
線型独立(1次独立)性や係数の「一意性」の利用法がイマイチわからない人が多いのではないでしょうか。
ベクトルで s:(1-s) や t:(1-t) とおいて求める問題のことです。
線型性という言葉はどうでも良いですが使い方は非常に大切で覚えておくとベクトルは難しくありませんよ。
ベクトルの線型結合
ベクトルの線型結合という言葉にはあまりなじみがない人が多いかもしれません。
教科書でも大々的にあつかってはいませんので慣れていない人も多いでしょう。
でも安心して下さい。
意味は知らなくて構いません。w
そのそも線型性という言葉自体、あまり登場しませんから知らなくていい言葉なんです。
ただ、後々説明がいらないようにここで簡単に説明しておきます。
線型性という言葉はベクトルだけに使われる言葉ではありません。
定義を見るとものすごくややこしいです。
だからベクトルの線型性を簡単に説明すると、
\(k (\vec{a}+\vec{b})= k\,\vec{a}+k\,\vec{b}\)
のように「和の実数倍」が「別々に実数倍したものの和」になる。
ということ。としておいて良いです。
ここではベクトルの線型結合を定義にしておきます。
\(\color{red}{\fbox{ ベクトルの線型結合 }}\)
\(\,\vec{a}\,,\, \vec{b}\,\)を与えられたベクトルとするとき、
実数\(\,\alpha\,,\,\beta\,\)を用いて
\(\hspace{10pt}\alpha\,\vec{a}+\beta\,\vec{b}\)
で表されるベクトルを\(\,\vec{a}\,,\,\vec{b}\,\)の線型結合という。
線型独立(1次独立)の条件
もう一つ、線型独立または1次独立と呼ばれる2つのベクトルの条件も書きだしておきます。
(定義は大した説明は必要ありませが、大学でしっかりと学んでください。)
\(\color{red}{\fbox{ 2つのベクトルの線型独立の条件 }}\)
2つのベクトル\(\,\vec{a}\,,\, \vec{b}\,\)が線型独立であるための条件は
\(\,\vec{a}\,,\, \vec{b}\,\)が\(\,\vec{0}\,\)でなく、かつ、平行でないことである。
成分で表すとややこしくはなるのですが同じ意味なので書き出しておきます。
\(\color{red}{\fbox{ 2つのベクトルの線型独立の条件の成分表示 }}\)
\(\,\vec{0}\,\)でない平面のベクトル
\(\hspace{10pt}\,\vec{a}=(\,a_1\,,\,a_2\,)\,,\, \vec{b}=(\,b_1\,,\,b_2\,)\)
が線型独立であるための条件は
\(\hspace{10pt}a_1\,b_2-a_2\,b_1\)≠\(0\)
である。
これは\(\,\vec{0}\,\)でない\(\,\vec{a}\,,\, \vec{b}\,\)が平行である条件が
\(\hspace{10pt}a_1\,b_2-a_2\,b_1=0\)
なので平行でない条件は\(\hspace{10pt}a_1\,b_2-a_2\,b_1\)≠\(0\)です。
ベクトルにおいては線型性という言葉ではなく、もっと重要な事実があります。
線形結合で表したベクトルの係数の一意性
係数の一意性とは、
あるひとつのベクトルを線型独立な2つのベクトルで表したとき、
例えば、
\(\hspace{10pt} \overrightarrow{\mathrm{AP}} = 3\overrightarrow{\mathrm{AB}} + 2\overrightarrow{\mathrm{AC}}\)
が示す点\(\,\mathrm{P}\,\)はただ1つに定まる、
ということ。
逆に点\(\,\mathrm{P}\,\)を
ベクトル \(\overrightarrow{\mathrm{AP}} = s\overrightarrow{\mathrm{AB}} + t\overrightarrow{\mathrm{AC}}\)
と表したとき、
\(s\) および \(t\) はただ1つの組でしか表せないという、
「係数の一意性」の方がはるかに重要だと思えます。
ということでここからは教科書にある方法で説明します。
ベクトル係数の一意性を利用する
もう一度問題を見てみます。
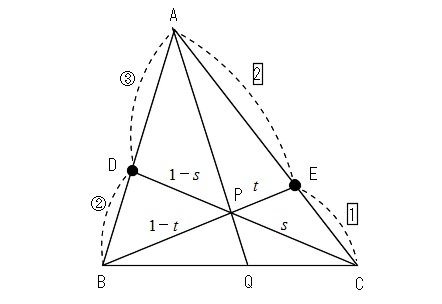
△ABCにおいて、辺ABを3:2に内分する点をD、辺ACを2:1に内分する点をEとし、線分BE、CDの交点をPとする。
また、線分APの延長がBCと交わる点をQとする。
このとき、 \( \overrightarrow{\mathrm{AP}}\) を \( \overrightarrow{\mathrm{AB}} , \overrightarrow{\mathrm{AC}}\) で表せ。
また、AP:PQ を求めよ。
別のところで説明しましたが、
メネラウスの定理ですぐにでてくるのですが、
ベクトル \( \overrightarrow{\mathrm{AP}}\) を使って求めてみましょう。
\(\,\mathrm{Q}\,\)は\(\,\mathrm{AP}\,\)の延長上にあるので
\( \overrightarrow{\mathrm{AQ}} = t \overrightarrow{\mathrm{AP}}\)
とおけます。
ここで
で求めたように
\(\hspace{10pt} \displaystyle \overrightarrow{\mathrm{AP}} = \frac{1}{3}\overrightarrow{\mathrm{AB}}+\frac{4}{9}\overrightarrow{\mathrm{AC}}\)
から
\(\begin{eqnarray} \displaystyle
\overrightarrow{\mathrm{AQ}}&=& t\,\left(\frac{1}{3}\overrightarrow{\mathrm{AB}}+\frac{4}{9}\overrightarrow{\mathrm{AC}}\right)\\
&=& \frac{1}{3}t\overrightarrow{\mathrm{AB}}+\frac{4}{9}t\overrightarrow{\mathrm{AC}}
\end{eqnarray}\)
となりますが、点\(\,\mathrm{Q}\,\)は,\(\,\overrightarrow{\mathrm{AB}}\,,\,\overrightarrow{\mathrm{AC}}\,\)の終点を結ぶ直線上にあるので、
\(\hspace{10pt}\displaystyle \frac{1}{3}t+\frac{4}{9}t=1\) ・・・☆
これから
\( \hspace{10pt}\displaystyle t=\frac{9}{7}\)
つまり、\(\,\mathrm{AP:AQ=7:9}\,\) であり、
\(\,\mathrm{AP:PQ=\underline{ 7:2 }}\,\)
図を書いて確認してください。
(下に図はありますが自分で線分比を書き込んで確認してください。)
\( \overrightarrow{\mathrm{AP}} , \overrightarrow{\mathrm{AQ}}\) ともに
\(\vec{a} , \vec{b}\) を用いて、一通りにしか表すことは出来ません。
これが線型独立なベクトルによる係数の一意性です。
☆:
2つのベクトル \( \vec{a} , \vec{b}\) の終点を結んだ直線上の点を表すベクトル \( \vec{p}\) を、
\( \vec{p} =\color{red}{ s}\,\vec{a}+\color{red}{ t}\,\vec{b}\) とすると、
\(\Large{\color{red}{\hspace{7pt} s+t = 1}} \)
となります。
空間では、3つのベクトルの終点を通る平面上にあるベクトル \( \vec{p}\) を、
\( \vec{p} =\color{red}{ s}\,\vec{a}+\color{red}{ t}\,\vec{b}+\color{red}{ u}\,\vec{c}\)
としたとき、
\( \Large{\color{red}{\hspace{7pt}s+t+u=1}}\)
となりますが、これらの事実はよく使われます。
覚えておいて下さい。
さて、ベクトルの線型性を使った方法も示しておきます。
1つのベクトルを文字を使って二通りに表す
先程説明したように平面上の1つのベクトル \( \vec{u}\) は、
線型独立なベクトル \( \vec{a} , \vec{b}\) を用いて、
\(\hspace{10pt} \vec{u} = s\vec{a}+t\vec{b}\)
と表せますが、
これを満たす \( s , t\) の組はたった一通りしかありません。
これが一意性ですね。
(定理です。「係数の一意性」といいますが日本語より事実を覚えて。)
簡単に言うと、 \( \vec{u}\) を
\( \vec{u} = \color{red}{ s}\,\vec{a}+\color{blue}{ t}\,\vec{b}\)
\( \vec{u} = \color{red}{ m}\,\vec{a}+\color{blue}{ n}\,\vec{b}\)
と二通りに表したとすると、
\( \color{red}{ s=m} , \color{blue}{ t=n}\) となるという、
「恒等式」や「複素数の相等条件」と同じようなものです。
この定理を利用します。
\(\mathrm{BP : PE} =(1-t) : t\)
\(\mathrm{DP : PC} =(1-s) : s\)
\(\displaystyle \overrightarrow{\mathrm{AP}} = t\overrightarrow{\mathrm{AB}}+(1-t)\frac{2}{3}\overrightarrow{\mathrm{AC}}\) ・・・②
\(\displaystyle \overrightarrow{\mathrm{AP}} = \frac{3}{5}s\overrightarrow{\mathrm{AB}}+(1-s)\overrightarrow{\mathrm{AC}}\) ・・・③
と二通りに表せますが、
このベクトルは同じものを表すので
\(\hspace{10pt}\displaystyle t=\frac{3}{5}s , \frac{2}{3}(1-t)=(1-s)\)
の両方程式を満たすことから \( s\,,\,t \) が求まり、
②または③に \( s \,,\, t \) を戻せば \( \overrightarrow{\mathrm{AP}}\) は求まります。
どちらでも同じになることを確認してみて下さい。
(一意性の確認)
この後は、
で示したように \( \overrightarrow{\mathrm{AQ}}\) を求めて、\(\,\mathrm{AP:QP}\,\) は求まります。
この2つの文字を利用した問題は随分前からずっと出題されています。
定理だから使いなさいよ。
ということでしょう。
それと、
「終点を結んだ直線、平面上の点のベクトルの係数の和が1になる」
ことも同じくらいの頻度で聞かれますので要チェックですよ。
まとめ
ベクトルと幾何は切り離せない関係があります。
幾何にたよらなくても解ける、
というようになるにはある程度訓練が必要でしょう。
先ずは
「2つのベクトル線型独立の条件」
と
係数の一意性
だけでも覚えておくとベクトルが少しは理解できますよ。
厳密な数学が勉強したい人は大学で深く勉強するとして、
共通テストや試験すべてで少しでもいいから点数を増やしたいという人はこの基本からにして下さい。