等差数列の和にシグマを使った計算方法の練習問題を取り上げて説明しておきます。数列で使うシグマは「和」を意味するので等差数列にだけ使えるとか、限定的なものではありません。シグマで表すことと計算することは違いますので実際に手を動かして確認しておいてください。
等差数列に使ったΣの計算方法
『Σの使い方』(表し方)のページで紹介した練習問題の解説をしながら進めます。
練習問題を見て、方針が立てられるようになれば、
後は処理する計算力(文字式の処理能力)となりますので、
計算が遅いと自分で感じる人は十分な訓練をしておくと良いですね。
ここは計算力に差がでるところです。
<数列の和の記号導入>
漸化式以降で使う予定だったのですが、ここで簡単に導入しておきます。
初項から第 \(n\) 項までの和を \( S_n\) と表します。
初項から第 \(n+1\) 項までの和は \( S_{n+1}\) 、
初項から第 \(n-1\) 項までの和は \( S_{n-1}\) となります。
「初項から」というのは変わりません。
等差数列の和の公式で求める場合
初項\(\,1\,\),公差\(\,3\,\)の等差数列の初項から第\(\,n\,\)項までの和 \(\,S_n\,\) を求めよ。
「シグマの使い方」の例題1の中で説明していますのでここでは簡単に済ませておきます。
ただ、
・等差数列といわれれば等差数列の和の公式を使い、
・\(\Sigma\) で表されれば \(\Sigma\) の計算公式を使う、
という場合が多いと思いますが、
「数列が何なのか」「何の和なのか」を見ることが大切で、
計算方法はどちらでも良いのです。
重要なのは、
\(\hspace{10pt}S_n=1+4+7+\cdots+(3n-2)\)
となっていることを確認することです。
等差数列の和として計算してみます。
等差数列の \(n\) 項の和は初項 \(a\) ,公差 \( d\) とすると
\(\displaystyle \color{red}{S_n=\frac{n}{2}\{2a+(n-1)d\}}\)
でした。

を書き出せば公式はいらない、
という説明もしてありますので必要ないとは思いますが、
\(\begin{eqnarray}\displaystyle
S_n&=&\frac{n}{2}\{a+a+(n-1)d\}\\
&=&\frac{n}{2}\,(a+\ell\,)
\end{eqnarray}\)
初項\(\,a\,\)と末項\(\,\ell\,\)を足して項数の半分をかける
ことと同じであるというのは思い出しておいてください。
シグマで表せても計算方法を忘れていては答えまで出ませんからね。
どちらでも良いですが、代入するだけなので自分でやって見てください。
\(\hspace{10pt}\displaystyle S_n=\frac{n}{2}(3n-1)\)
と結果がなっていれば正解です。
初項\(\,1\,\),公差\(\,3\,\)の等差数列の初項から第\(\,10\,\)項までの和を求めよ。
これは上限が\(\,10\,\)となっているので、
「等差数列の初項から第\(\,10\,\)項までの和」
です。
\(\begin{eqnarray} \displaystyle
S_{10}&=&1+4+7+\cdots+28\\
&=&\frac{10}{2}(1+28)\\
&=&5\times 29=145 ・・・①
\end{eqnarray}\)
※
①について
初項 \( a\) ,末項 \( \ell\) ,項数 \( n\) のときの和は、
\(\hspace{10pt}\displaystyle \color{red}{S_n=\frac {n}{2}(a+\ell)}\)
です。
シグマ計算で求める場合
\(\sum\) の計算公式を使えば
\(\hspace{10pt} a_n=3n-2\)
の初項から第\(\,10\,\)項までの和なので、
\(\begin{eqnarray}\displaystyle
S_{10}&=&\sum_{k=1}^{10}\,(3k-2)\\
&=&3\color{red}{\sum_{k=1}^{10} k}-\color{blue}{\sum_{k=1}^{10} 2}\\
&=&3\cdot \color{red}{\frac{1}{2}\cdot 10\cdot(10+1)}-\color{blue}{2\cdot 10}\\
&=&145
\end{eqnarray}\)
下限が1では無い場合
初項\(\,1\,\),公差が\(\,3\,\)の等差数列の第\(\,2\,\)項から第 \( n\) 項までの和を求めよ。
\( k\,\) が\(\,2\,\)から始まっていることに注意が必要です。
\(\sum\,\)の公式はそのままでは使えません。
\(\sum\,\)の計算公式は、下限が\(\,k=1\,\)のときにだけそのまま使える限定公式ですからね。
\(\begin{eqnarray}
S&=&a_2+a_3+a_4+\cdots+a_n\\
&=&4+7+10+\cdots+(3n-2)\end{eqnarray}\)
となっています。
これは \( k=2\) から \( n\) まで変化するので項数は \( n-1\) です。
初項が\(\,4\,\),公差が\(\,3\,\)の等差数列\(\,n-1\,\)項分の和なので、
等差数列の和の公式を利用するなら
\(\begin{eqnarray}\displaystyle
S&=&\frac{n-1}{2}(4+3n-2)\\
&=&\frac{1}{2}(n-1)(3n+2)
\end{eqnarray}\)
もとの問題のまま \( \sum\) の計算公式を利用しようと思うなら、
\( \begin{eqnarray}\displaystyle
S&=&(a_1+a_2+a_3+a_4+\cdot +a_n)-(a_1)\\
&=&\{1+4+7+\cdots+(3n-2)\}-(1)
\end{eqnarray}\)
と \( k=1\) の値「 \(\,a_1\,\)を一度足して、後で引けば」、
和は変わらないので \( \sum\) の公式が利用できる形に変形できます。
\(\begin{eqnarray} \displaystyle
S&=&\sum_{k=1}^n (3k-2)-\sum_{k=1}^1 (3k-2)\\
&=&\sum_{k=1}^n (3k-2)\color{red}{-(1)}
\end{eqnarray}\)
ここで後ろの「\(\,\color{red}{-(1)}\,\)」はシグマには関係していません。
\(\begin{eqnarray} \displaystyle
S&=&\color{red}{3\sum_{k=1}^n k}-\color{blue}{\sum_{k=1}^n\,2}-(1)\\
&=& \color{red}{3\cdot\frac{1}{2}n(n+1)}-\color{blue}{2n}-1\\
&=&\frac{1}{2}\{3n(n+1)-4n-2\}\\
&=&\frac{1}{2}(3n^2-n-2)\\
&=&\frac{1}{2}(n-1)(3n+2) ・・・②\end{eqnarray}\)
※
②の処理は因数分解そのものです。
中学数学の頃にコツは得ていると思いますが、
分数を含む多項式では「分母の最小公倍数でくくる」のがはやく処理する基本でしたよね。?
試験の時間が足りないという人はこういうところの処理が下手です。笑
計算が遅いのではなく、処理のしかたがちょっと要領よくできていないだけかもしれませんよ。
上限が一般的でない場合
初項1,公差が3の等差数列の初項から第 \(n-1\) 項までの和を求めよ。
数列 \(a_n\) で使う添え字 \( n\) は、
\(\,n\,\)が\(\,n-1\,\)に変われば\(\,n\,\)のすべてに\(\,n-1\,\)
\(\,n\,\)が\(\,n+1\,\)に変われば\(\,n\,\)のすべてに\(\,n+1\,\)
を代入すればいいのです。
たとえば、
\(\hspace{10pt}a_n=n^2+3n\)
のとき
\(\hspace{10pt} a_{\color{red}{n+1}}=(\color{red}{n+1})^2+(\color{red}{n+1})\)
のように代入すれば関係式は成り立ちます。
※
代入は(かっこ)を付けるとミスが減ります。
第\(\,n-1\,\)項は、
\(\begin{eqnarray}
a_{n-1}&=&3(n-1)-2\\
&=&3n-5
\end{eqnarray}\)
なので\(\,n-1\,\)項までの和は
\(\begin{eqnarray}
S_{n-1}&=&1+4+7+\cdots+\{3(n-1)-2\}\\
&=&1+4+7+\cdots+(3n-5)
\end{eqnarray}\)
等差数列の和とすれば、
初項\(\,\color{red}{1}\,\),末項\(\,\color{blue}{3n-5}\,\),項数\(\,\color{magenta}{n-1}\,\)だから
\( \begin{eqnarray} \displaystyle
S&=&\frac{\color{magenta}{n-1}}{2}(\color{red}{1}+\color{blue}{3n-5})\\
&=&\frac{1}{2}(n-1)(3n-4)
\end{eqnarray}\)
これは\(\,k=1\,\)から始まっているので\(\,\sum\,\)の計算公式が使えます。
\(\begin{eqnarray}\displaystyle
S&=&\sum_{k=1}^{n-1} (3k-2)\\
&=&3\sum_{k=1}^{n-1} k-\sum_{k=1}^{n-1} 2 ・・・\,(\,C_4-1\,)
\end{eqnarray}\)
添え字は文字の位置にそのまま入れかわるので、
\(\hspace{10pt} \displaystyle \sum_{k=1}^\color{blue}{n} k=\frac{1}{2}\color{blue}{n}(\color{blue}{n+1})\)
という公式の場合
\(\hspace{10pt} \displaystyle \sum_{k=1}^{\color{red}{n-1}} k=\frac{1}{2}(\color{red}{n-1})\{(\color{red}{n-1})+1\}\)
のように代入すれば良いだけです。
\(\,(\,C_4-1\,)\,\)を続けると、
\(\begin{eqnarray} \displaystyle
S&=&3\sum_{k=1}^{n-1} k-\sum_{k=1}^{n-1} 2\\
&=&3\cdot \frac{1}{2}(n-1)\{(n-1)+1\}-2\cdot(n-1)\\
&=&(n-1)\left(\frac{3}{2}n-2\right)\\
&=&\frac{1}{2}(n-1)(3n-4)
\end{eqnarray}\)
(分母の最小公倍数を係数として前に出すとすっきりしませんか?)
というようにシグマの計算公式を利用すれば機械的に答えが出ます。
ちょっと「計算頼り」ではありますが考えなくて良いですね。笑
初項\(\,1\,\),公差が\(\,3\,\)の等差数列の初項から第 \(\,2n\,\) 項までの和を求めよ。
下限が\(\,k=1\,\) からなので\(\,\sum\,\)の計算公式が使えます。
上限が\(\,2n\,\)なので、計算公式\(\,n\,\)の代わりに\(\,2n\,\)を代入すれば良いだけです。
\(\begin{eqnarray}\displaystyle
S_{2n}&=&\sum_{k=1}^{2n} (3k-2)\\
&=&3\sum_{k=1}^{2n} k-\sum_{k=1}^{2n} 2\\
&=&3\cdot \frac{1}{2}(2n)\{(2n)+1\}-2\cdot (2n)\\
&=&3\,n\,(\,2n+1\,)-4\,n\\
&=&n\,(\,6\,n+3-4\,)\\
&=&n\,(\,6\,n-1\,)
\end{eqnarray}\)
「等差数列の和」と見るなら、
初項\(\,1\,\)
末項 \( a_{2n}=1+3(\,2\,n-1\,)=6\,n-2\)
で項数が\(\,2\,n\,\)項なので
\(\begin{eqnarray} \displaystyle
S_{2n}&=&\frac{2\,n}{2}(\,1+6n-2\,)\\
&=&n\,(\,6\,n-1\,)
\end{eqnarray}\)
シグマ計算か等差数列の和の公式のどちらかで進めると思うのでそのときの結果を確認をします。
\( n=1\) のとき
初項と第\(\,2\,\)項を足して
\(\hspace{10pt} S_2=1+4\,=5\)
また、求めた和の式に代入して
\(\hspace{10pt} S_2=1\times 5\,=5\)
で一致します。
\( n=2\) のとき
\(\hspace{10pt} S_4=1+4+7+10\,=22\)
と
\(\hspace{10pt} S_4=2\times 11\,=22\)
で一致します。
だいたい間違えているとすれば \(n=1\) の時点で違っています。笑
上限、下限ともに一般的じゃない場合
初項\(\,1\,\),公差が\(\,3\,\)の等差数列の第 \(n+1\) 項から第 \( 2n\) 項までの和を求めよ。
何度も言ってきていますが、\(\,\sum\,\)の計算公式は下限が\(\,k=1\,\)の場合のみ使えます。
この問題は下限が\(\,n+1\,\)なので、そのままでは使えません。
\(\,\sum\,\)の意味から書き出すと、
数列\(\,a_n=3n-2\,\)
の
第\(\,n+1\,\)項目から第\(\,2n\,\)項までの和
なので
\(\begin{eqnarray}
S&=&a_{n+1}+a_{n+2}+a_{n+3}+\cdots+a_{2n-1}+a_{2n}\\
&=&\sum_{k=n+1}^{2n}(\,3k-2\,)\\
&=&\{3(n+1)-2\}+\{3(n+2)-2\}+\cdots+\{3(2n)-2\}\\
&=&(3n+1)+{3n+4}+\cdots+(6n-2)
\end{eqnarray}\)
ここで一度シグマから離れて差数列の和として見れば、
初項\(\,3n+1\,\),末項\(\,6n-2\,\),項数\(\,n\,\)の等差数列の和
だから
\(\begin{eqnarray}\displaystyle
S&=&\frac{n}{2}\{(\,3n+1\,)+(\,6n-2\,)\}\\
&=&\frac{1}{2}n\,(\,9n-1\,)
\end{eqnarray}\)
と求めることは簡単になります。
しかし、
ここではシグマを使えるようになることが目的です。
ただ、\(\sum\,\)の計算公式を利用するとなるとちょっとだけ工夫が必要です。
といっても計算公式が使えるように\(\,k=1\,\)を下限とすれば良いだけなので、
慣れれば普通の手段になるので覚えていきましょう。
初項から第\(\,2n\,\)項までの和は
\( S_{2n}=a_1+\cdots+a_n+a_{n+1}+\cdots+a_{2n}\)
「求めたい和」は後半の
\(S=a_{n+1}+a_{n+2}+\cdots+a_{2n}\)
の部分なので\(\,S_{2n}\,\) から\(\,S_n\,\)を引いた
\(S=\color{red}{S_{2n}}-\color{blue}{Sn}\\
\hspace{6pt}=\color{red}{(a_1+\cdots+a_n+a_{n+1}+\cdots+a_{2n})}\\
\hspace{20pt}-\color{blue}{(a_1+\cdots+a_n)}\)
ですよね。
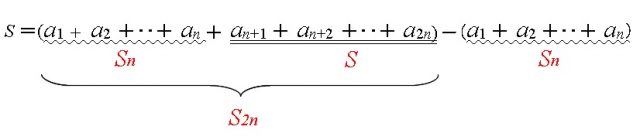
\( S_n\) の部分は足して、引いているので和に影響はありません。
前の(かっこ)は初項 \( a_1\) ( \( k=1\) のとき)から第 \( 2n\) 項までの和、
後ろの(かっこ)は初項( \(k=1\) のとき)から第 \(n\) 項までの和、
として両方に\(\,\sum\,\)の計算公式が使えるようになります。
\(\displaystyle \sum_{k=1}^n (3k-2)\)
は練習\(\,1\,\)で、
\(\displaystyle \sum_{k=1}^{2n} (3k-2)\)
は練習\(\,5\,\)で、
すでに求めているので、途中の\(\,\sum\,\)の展開部分を省略すると、
(自分で計算できるように!)
\(\begin{eqnarray}\displaystyle
S&=&\sum_{k=1}^{2n} (\,3k-2\,)-\sum_{k=1}^n (\,3k-2\,)\\
&=&n(\,6n-1\,)-\frac{1}{2}n(\,3n-1\,)\\
&=&n\left\{(\,6n-1\,)-\frac{1}{2}(\,3n-1\,)\right\}\\
&=&\frac{1}{2}n\{2(\,6n-1\,)-(\,3n-1\,)\}\\
&=&\frac{1}{2}n(\,12n-2-3n+1\,)\\
&=&\frac{1}{2}n(\,9n-1\,)
\end{eqnarray}\)
確認:
等差数列の和としても求めているなら良いですが、
普通は両方やらないだろうから\(\,n=1\,\)のときだけでも入れて見ると良いですよ。
\(\,n=1\,\)とすると、
「第\(\,2\,\)項から第\(\,2\,\)項までの和を求めよ。」
となるので第\(\,2\,\)項のみを求めてみれば良いだけです。
\( a_2=3\cdot 2-2=4\)
\(\displaystyle S=\frac{1}{2}\cdot 1\cdot(9-1)=4\)
で一致しています。
このように計算公式を利用することはできます。
ただし、
\(\color{red}{定数 , k , k^2 , k^3 以外では\\
\,\sum\,の計算公式は使えませんよ。}\)
具体的に和の形がどうなっているか、確認することが大切なのです。
等差数列についてはここで一度区切ります。
シグマは等比数列にも当然用いる記号ですよ。
数学の記号なので当たり前のことですが数列全般で用いる記号は同じです。
