確率の中にある期待値とは何なのか、定義と求め方を分かり易い数字を使って説明します。
H27年度の新課程から確率の分野ではなく統計分野に移されていますが、
期待値の考え方は場合の数、確立の問題を解くときの大きなヒントになるのでチェックしておいた方が良いです。
期待値とは?
期待値は「統計」分野にあり、「確率変数の平均値」として一般化した形で学ぶことになります。
しかし、そんな難しい言葉はいらないので簡単な言葉と数字で説明します。
例えば、
10本のくじがあって、当たりくじが2本入っているとしましょう。
「当たりくじを引くと500円、ハズレくじを引くと100円」
の賞金がもらえるとします。
このとき賞金の合計は、
当たりくじが2本なので \(500\times 2=1000\)
ハズレくじが8本なので \(100\times 8=800\)
賞金総額は \(1000+800=1800\) 円です。
10本のくじの賞金総額が \(1800\) 円なので、
1本当たりの賞金額は、\(\displaystyle\frac{1800}{10}=180\) 円となります。
これが「期待値」です。
当たれば \(500\) 円、はずれれば \(100\) 円ですが、
平均した1本当たりの賞金は \(180\) 円です。
このように「期待できる平均賞金額」のことを期待値というのです。
金額の期待値は「期待金額」ということもあります。
これは別の求め方があります。
1本当たりの賞金額は、
\( \displaystyle \frac{500\times 2+100\times8}{10}=180\)
として計算していますがちょっと見方を変えると
\( \displaystyle \frac{500\times 2+100\times8}{10}\\ \\
=500\times \displaystyle \frac{2}{10}+100\times \displaystyle \frac{8}{10}\)
これは、
(当たりの賞金)×(当たる確率)+(はずれの賞金)×(はずれる確率)
となっています。
このように、「(各賞金)×(それぞれの確率)の『和』」で期待値を求めることができるのです。
定義として一般的にも表しておきます。
ところで「はずれても100円」の賞金なんてくじはあるのか?と思いますよね。
このくじを引く前に「300円でくじを買っている」のです。
売る側にすれば10本売れれば3000円の売り上げです。
賞金総額覚えてます?1800円です。
売った人は確実に1200円儲けていることになります。笑
このくじの還元率は60%ですが、日本の宝くじの場合もっと低くて50%以下ですよ。
つまり、300円の宝くじを買った場合の期待値は150円より少ないです。
期待値の定義
【期待値の定義】
一般にある試行において、
変数\(X\)が \( x_1,x_2,\cdots x_n\) のいずれかの値になり、
\(x_1\) になる確率が \(p_1\) ,
\(x_2\) になる確率が \(p_2\) ,
\(\cdots\) ,
\(x_n\) になる確率が \(p_n\) であるとき、
\(\large{ \color{red}{m=x_1p_1+x_2p_2+\cdots x_np_n}}\)
のことを\(X\)の期待値という。
サイコロで計算してみましょう。
サイコロの出目\(X\)は1,2,3,4,5,6のどれかです。
このXに対する確率はすべて同じ \(\displaystyle \frac{1}{6}\) です。
よって、サイコロの出目\(X\)の期待値 \( m\) は
\( m=1\times \displaystyle \frac{1}{6}+2\times \displaystyle \frac{1}{6}+3\times \displaystyle \frac{1}{6}+4\times \displaystyle \frac{1}{6}+5\times \displaystyle \frac{1}{6}+6\times \displaystyle \frac{1}{6}\\ \\=\displaystyle \frac{21}{6}=\displaystyle \frac{7}{2}=3.5\)
となります。
確率と期待値問題の関係
確率だけを求めるなら期待値問題は必要無いかというとそうではありません。
基本的に、期待値を求めるには「すべての場合を見る」必要があります。
これは確率を求める際にも大切なポイントになるのです。
2つのさいころを投げて出た目の最大値をXとする。
X≦4となる確率、X=5となる確率をそれぞれ求めよ。
また、Xの期待値を求めよ。
「2つのサイコロを」とか「同時に」とか良く問題にありますが、
同時に投げようが、1個ずつ投げようが同じです。
同時にサイコロ投げてみても、同時にぴたっと止まることなんてないんです。
一つ目が4以下になる確率は \(\displaystyle\frac{4}{6}=\frac{2}{3}\)
二つ目が4以下になる確率も \(\displaystyle \frac{4}{6}=\frac{2}{3}\)
よってX≦4となる確率は \(\displaystyle \frac{2}{3}\times \frac{2}{3}=\frac{4}{9}\) として構いません。
中学生なら、2つのサイコロを投げるときは表を作るといいですよ。
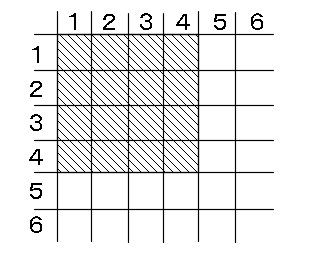
表の網目部分ですので \(\displaystyle \frac{16}{36}=\frac{4}{9}\) とすることも出来ますが同じことです。
確率の積を知ったならかけ算した方が早い。(独立試行の乗法定理)
X=5となるとき、これは重複試行の例題3でもやりました。
X≦5からX≦4を引けばどちらかに5が出ていることになります。
X≦5となる確率は \(\displaystyle \frac{5}{6}\times \frac{5}{6}=\frac{25}{36}\)
なのでX=5となる確率は \(\displaystyle \frac{25}{36}-\frac{16}{36}=\frac{9}{36}=\frac{1}{4}\)
さて、
期待値ですが、統計分野(ⅡB範囲)に回されましたが重要な点があるのでやっておきます。
※「期待値」は数ⅡBに移行されましたので必要ありません。
期待値は、「(確率変数X)《ここではサイコロの出目です》×(確率)の総和」です。
式で表すと、\( X=1,2,\cdots ,6\) までの確率をそれぞれ、\( p_1,p_2,\cdots p_6\) とすると、
期待値Eは
\( E=1\times p_1+2\times p_2+3\times p_3+4\times p_4+5\times p_5+6\times p_6\)
となります。
重要なのは、すべての場合の確率を出す、という作業です。
分かっているのは先に求めた \(\displaystyle p_5=\frac{9}{36}\) だけです。
\( p_1\) は2つのサイコロの「最大値が1」=「両方1」の確率ですよ。
\( p_1=\displaystyle \frac{1}{36}\) , \(p_2=\displaystyle \frac{3}{36}\) , \(p_3=\displaystyle \frac{5}{36}\) , \(p_4=\displaystyle \frac{7}{36}\) , \(p_5=\displaystyle \frac{9}{36}\) , \(p_6=\displaystyle \frac{11}{36}\)
となります。
これを(自分で)やらないと意味がないのです。
センター試験でもずっとここが問われて来ました。この作業は自分でやりましょう!
何故 \( p_5\) において約分していないかというと、
「確率の総和が1」になっていることを確認しやすくするためです。
(すべての場合の確率の和は1となるから。必ず何かが起きる。)
よって期待値は、
\( E=1\times \displaystyle \frac{1}{36}+2\times \displaystyle \frac{3}{36}+3\times \displaystyle \frac{5}{36}+4\times \displaystyle \frac{7}{36}+5\times \displaystyle \frac{9}{36}+6\times \displaystyle \frac{11}{36}\\ \\
=\displaystyle \frac{1\cdot 1+2\cdot 3+3\cdot 5+4\cdot 7+5\cdot 9+6\cdot 11}{36}\\ \\
=\displaystyle \frac{161}{36}\)
期待値に限らず、すべての事象、場合を書き出すって、重要ですよ。
順列、組合せから見ておくと良いかもしれません。