2018年度、平成30年度のセンター試験の数学ⅠAの第2問の解説です。
三角比とデータの分析の範囲ですが問題数の割に内容を読み取る分量としては多いです。
昨年度と比べるとデータの分析は散布図と箱ひげ図をしっかり読み取れば分かりやすい問題にはなっていました。
問題は大学入試センター公式ページにもあります。
第2問(必答)
ここも必答です。
三角比はちゃちゃっと終わらせて、データの分析に対応できたかがポイントです。
ただ、当たり前のことだけど図を書かないと苦しい三角比でしたね。
しかも図の位置関係が分かりにくかったのではないでしょうか。
ある程度の図が書けたら、問題を解き進めていくと位置関係が絞られてきます。
〔1〕三角比(図形と計量)
四角形ですが円に内接はしていませんでした。
四角形ABCDにおいて、3辺の長さをそれぞれAB=5,BC=9,CD=3,対角線ACの長さをAC=6とする。
これらの長さは必ず使う数値なので図にかっきり分かるように書き込んでおくことです。
先ずは簡単な図でも良いので書いて見ましょう。
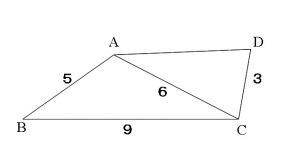
う~ん、定まりませんね。
ということで問題に入りましょう。
\( \angle {ABC}\) つまり \( \angle{B}\) についての \( \sin\,,\,cos\) の値です。
親切に余弦定理を使うことが分かるように \( \cos \angle{ABC}\) を先に書いてくれています。
\( \cos \angle{ABC}=\displaystyle \frac{5^2+9^2-6^2}{2\times 5\times 9}\\ \\
=\displaystyle \frac{25+81-36}{2\times 5\times 9}\\ \\
=\displaystyle \frac{70}{2\times 5\times 9}\\ \\
=\displaystyle \frac{\fbox{7}}{\fbox{9}}\)
ア:7 イ:9
これから \( \angle{ABC}\) は鋭角です。
\( \sin^2\theta+\cos^2\theta=1\\ \\
\Leftrightarrow \hspace{10pt} \sin^2\theta=1-\cos^2\theta\)
で三角形の内角に対しては \( \sin\angle {ABC}>0\) だから正の平方根をとって
\( \sin\angle{ABC}=\sqrt{1-\left(\displaystyle \frac{7}{9}\right)^2}\\ \\
=\sqrt{1-\displaystyle \frac{49}{81}}=\sqrt{\displaystyle \frac{32}{81}}=\displaystyle \frac{\fbox{4}\sqrt{\fbox{2}}}{\fbox{9}}\)
ウ:4 エ:2 オ:9
それにしても図を書くスペースと計算するスペースを十分に与えてくれている出題者の優しさが伝わります。
次です。
四角形ABCDが台形の場合についてです。
もとの条件では台形かどうかも分かりませんでしたからこれで少しやりやすくなるかもしれません。
ただし、等脚台形ではありませんよ。
(辺AD=9のときに等脚台形になりますがAC=6があるのでAD=9にはなりようがありません。)
台形になるのは
ⅰ)「ABとCDが平行となる」
ⅱ)「ADとBCが平行となる」
の2つがあります。
ⅰ)の場合
\(\,\mathrm{A}\,\)から辺\(\,\mathrm{BC}\,\)に垂線を下ろしたときの長さは、
\( AB\cdot \sin\angle{ABC}=5\cdot \displaystyle \frac{7}{9}=\displaystyle \frac{35}{9}\)
これは \( CD=3\) より長いのでABとCDが平行となることはあり得ません。
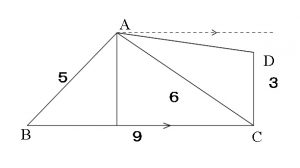
これが誘導に入っています。
\(\mathrm{CD} \fbox{<} AB\cdot \sin\angle{ABC}\)
だから台形になるとすればⅱ)の「ADとBCが平行となる」場合だということです。
カ:⓪ キ:④
これは実際にあります。
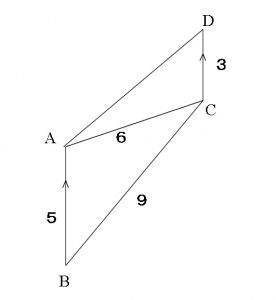
したがって
BD=
でました、「したがって」。
マーク式の問題ではこれは怖い言葉です。
どこからどこまでにしたがうのか、分かりにくいです。
この場合、長さなどの初期条件と台形でABとCDが平行ということすべてですね。
長さを求める方法は、相似、三平方、余弦定理を思い出せるでしょうか?
相似は使いづらい気がする。
三平方は面積から使えそう。
もう一度余弦定理で \( \cos\angle{BAC}=\cos\angle{ACD}\) を求めるというのもどうか。
迷うくらいなら突っ走っても良いですが、
「面積利用していない」という理由から強引に面積を使うことを決めると、
\(\begin{eqnarray}\displaystyle
\triangle{\mathrm{ABC}}&=& \frac{1}{2}\cdot \mathrm{AB}\cdot \mathrm{BC} \cdot \sin\angle{\mathrm{ABC}}\\ \\
&=& \frac{1}{2}\cdot 5\cdot 9\cdot \displaystyle \frac{4\sqrt{2}}{9}\\ \\
&=&10\sqrt{2}\end{eqnarray}\)
これを利用して三角形の高さ、つまり辺ABと辺CDの距離を求めます。
辺ABと辺CDの距離を \( h\) とすると底辺が\(\,\mathrm{AB}\,\)の三角形とみて
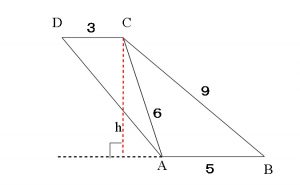
\( \triangle{\mathrm{ABC}}= \displaystyle \frac{1}{2}\cdot \mathrm{AB}\cdot h=10\sqrt{2}\\ \\
\Leftrightarrow \hspace{10pt} \displaystyle \frac{1}{2}\cdot 5\cdot h=10\sqrt{2}\\ \\
\Leftrightarrow \hspace{10pt} h=4\sqrt{2}
\)
ここで図の三角形\(\,\mathrm{ABE}\,\)に三平方の定理を利用して、
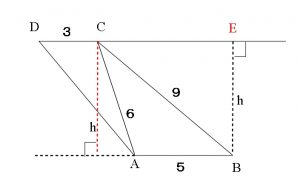
試験場でこんなきれいな図は書けません。
だいたいの位置関係さえつかんでいれば大丈夫です。
\( \mathrm{BE^2+CE^2=BC^2}\)
だから
\( (4\sqrt{2})^2+\mathrm{CE^2}=9^2\\ \\
\Leftrightarrow \hspace{10pt} \mathrm{CE^2}=81-32=49\)
これから \( \mathrm{CE=7}\) です。
今度は三角形\(\,\mathrm{BDE}\,\)において三平方の定理を利用して、
\(\hspace{10pt} \mathrm{BD^2}=\mathrm{BR^2+DE^2}\\ \\
=(4\sqrt{2})^2+10^2\\ \\
=132\)
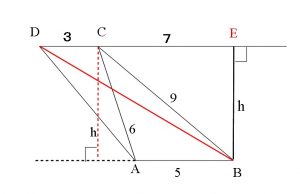
よって
\(\,\mathrm{BD}=\sqrt{132}\\ \\
=\sqrt{2^2\cdot33}=\fbox{2}\sqrt{\fbox{33}}\)
ク:2 ケコ:33
\(\,\mathrm{BD}\,\)を求めるときは、素因数分解すれば良いので上の様な変形は必要ないです。
図が書きにくくて、分かりにくかったかもしれませんが誘導に乗れば大した時間はかかりません。
ABとCDが平行なので、
\(\,\mathrm{∠ABC+∠BCD=180°}\,\)
と気がつけば
\(\begin{eqnarray}
\cos\angle{\mathrm{BCD}}&=&\cos(180^\circ-\angle{\mathrm{ABC}})\\ \\
&=&-\cos\angle{\mathrm{ABC}}
\end{eqnarray}\)
から\(\,\mathrm{△BCD}\,\)で余弦定理が使えます。
どっちでも良いです。
〔2〕データの分析
(1)(2)(3)とありますが、3問しかないのに、
文字がびっしり、図やグラフがびっしり、最後は意味は分からなくても展開して変形する問題。
とりつきにくかったかもしれません。
問題の中で基本用語を確認しているのでたった3問だけど量的には多いといって良いかもしれませんね。
「陸上競技大会」とかは関係ありません。
4つのグループデータがあります。
人数も300人前後ですが関係ありません。
(1)ヒストグラムと箱ひげ図の読み取りです。
(図は箱ひげ図の書き方)
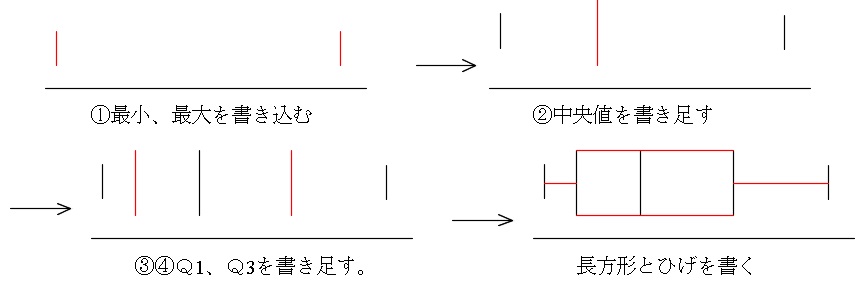
⓪ 四つのグループのうちで範囲が最も大きいのは、女子短距離グループである。
範囲を見れば良いのです。
範囲は「最大値-最小値」なので、
ヒストグラムでも箱ひげ図でもどちらでもかまいません。
箱ひげ図を見ると、
男子短距離(以後「男短」):\(\,202-152\,=\,50\,\)
男子長距離(以後「男超」):\(\,198-155\,=\,43\,\)
女子短距離(以後「女短」):\(\,187-145\,=\,42\,\)
女子長距離(以後「女長」):\(\,186-151\,=\,35\,\)
とそれぞれの範囲がでます。
範囲が1番大きいのは「男短」なので正しくない。
① 四つのグループのすべてにおいて、四分位範囲は12未満である。
四分位範囲は「\(\,\mathrm{Q_3\,-\,Q_1}\,\)」です。
箱ひげ図の色つき部分なので、長方形の上限と下限を見ればいい。
男短:\(\,186-176\,=\,10\,\)
男超:\(\,181-172\,=\,9\,\)
女短:\(\,174-165\,=\,9\,\)
女長:\(\,170-161\,=\,9\,\)
あれ?読み取り違いかな?
どこから\(\,12\,\)未満という数字になったのかわかりませんが、正しいです。
②男子長距離グループのヒストグラムでは、度数最大の階級に中央値が入っている。
これは「男長」のデータだけを見れば良いです。
度数の最大階級は「\(\,170\,\)cm以上\(\,175\,\)cm未満」
中央値は箱ひげ図の\(\,\mathrm{Q_2}\,\)から「\(\,176\,\)」
なので正しくない。
③ 女子長距離グループのヒストグラムでは、度数最大の階級に第1四分位数が入っている。
女長のデータだけを見ます。
度数最大の階級は「\(\,165\,\)cm以上\(\,170\,\)cm未満」
第1四分位数は\(\,\mathrm{Q_1}\,\)の「\(\,161\,\)」
なので正しくありません。
④ すべての選手の中で最も身長の高い選手は、男子長距離グループの中にいる。
全部のデータの中で最高身長は箱ひげ図の最大値から
「男短:\(\,202\,\)cm」
なので正しくありません。
⑤ すべての選手の中で最も身長の低い選手は、女子長距離グループの中にいる。
最も身長の低い選手は、箱ひげ図の最低値である
「女短:\(\,145\,\)cm」
なので正しくありません。
⑥ 男子短距離グループの中央値と男子長距離グループの第3四分位数は、ともに\(\,180\,\)以上\(\,182\,\)未満である。
それぞれを見つければ良いだけです。
男短の中央値\(\,\mathrm{Q_2}\,\):\(\,181\,\)
男長の第3四分位数\(\,\mathrm{Q_3}\,\):\(\,181\,\)
で同じで正しい。
サ:① シ:⑥
(2)
これは(1)から続いているようで別問題です。
身長: \( H\)
体重: \( W\)
\( X=\left(\displaystyle \frac{H}{100}\right)^2\)
\( Z=\displaystyle \frac{W}{X}\)
となっています。
何だかややこしいですが、\( X\) は身長をcm → mにして2乗しているだけ。
\( Z\) は体重を身長の2乗で割っているだけです。
とにかくややこしそうに見せるのが好きなセンター試験ですが、中身は
「データはながめるだけじゃ無く、しっかり読み取って計算してください。」
という作業自体は実用的な内容です。
ただ、今回は傾きが与えられているのでデータの意味が読み取れれば簡単です。
⓪ 四つのグループのすべてにおいて、\( X\) と \( W\) には負の相関がある。
正の傾き(正の相関)を与えてくれています。
どちらかというと傾きに沿った分布をしているので正しくない。
① 四つのグループのうちで \( Z\) の中央値が一番大きいのは、男子長距離グループである。
\(Z\) は \(\displaystyle \frac{W}{X}\) で求まる数値ですがこれは「傾き」とみることができます。
この箱ひげ図はそれぞれどのグループかを見分けておきましょう。
散布図の点を読み取ります。
例えば(a)の箱ひげ図は最大値が30以上あります。
ここで散布図の傾きの大きい \( l_4=30\) 上に近い点を見るのですよ。
この問題のポイントはここです。
\( Z\) の15から30くらいまでの値は傾きの大きさです。
散布図を見ると
男短の \(Z\):最大値は\(\,30\,\)くらいで、最小値は\(\,15~20\,\)
男長の \(Z\):最大値は\(\,30\,\)に近い、最小値は\(\,15~20\,\)
女短の \(Z\):最大値は\(\,25~30\,\)、最小値は\(\,15\,\)に近い
女長の \(Z\):最大値は\(\,20~25\,\)、最小値はほぼ\(\,15\,\)
これを箱ひげ図に合わせてみると
男短:(a)
男長:(c)
女短:(b)
女長:(d)
となります。
中央値が一番大きいのは(a)の男短なので正しくありません。
② 四つのグループのうちで \( Z\) の範囲が最小なのは、男子長距離グループである。
\( z\) の範囲はだいたいですが
(a): \(\,30-17.2\,=\,12.8\,\)
(b): \(\,27.2-15.6\,=\,11.6\,\)
(c): \(\,28.7-16.4\,=\,12.3\,\)
(d): \(\,23.3-15.2\,=\,8.1\,\)
よって範囲が最小なのは明らかに(d)の女長で正しくありません。
③ 四つのグループのうちで \( Z\) の四分位範囲が最小なのは、男子長距離グループである。
四分位範囲とは、簡単にいえば箱ひげ図の色塗り長方形の横幅です。
(a): \(\,24.2-21.6\,=\,2.6\,\)
(b): \(\,21.6-19.6\,=\,2\,\)
(c): \(\,21-19.1\,=\,1.9\,\)
(d): \(\,19.3-17.6\,=\,1.7\,\)
であり、最小なのは(d)の女長の感じ、少なくとも男短ではないので正しくない。
④ 女子長距離グループのすべての \( Z\) の値は25より小さい。
女長の箱ひげ図は(d)で最大値は\(\,23.2\,\)くらいです。
すべての \( Z\) 値は25より小さいので正しい。
⑤ 男子長距離グループの \(Z\) の箱ひげ図は(C)である。
もう答はでています。
正しい。
ス:④ セ:⑤
(3)
これは突然の問題で(1)(2)のデータは全く関係なさそうですよね。
全く関係ありません。
平均値
\( \bar{x}=\displaystyle \frac{x_1+x_2+\cdots +x_n}{n}\)
\( \bar{w}=\displaystyle \frac{w_1+w_2+\cdots +w_n}{n}\)
がどう関係するのか?
とりあえず
\( (x_1+x_2+\cdots +x_n)\bar{w}=n\bar{x}\bar{w}\)
「など」とあるので「など」を表しておきます。
\( \bar{x}=\displaystyle \frac{x_1+x_2+\cdots +x_n}{n}\\ \\
\Leftrightarrow \hspace{10pt} x_1+x_2+\cdots +x_n=n\bar{x}\)
両辺に \( \bar{w}\) かけると
\( (x_1+x_2+\cdots +x_n)\bar{w}=n\bar{x}\bar{w}\) ・・・①
\( \bar{w}=\displaystyle \frac{w_1+w_2+\cdots +w_n}{n}\\ \\
\Leftrightarrow \hspace{10pt} w_1+w_2+\cdots +w_n=n\bar{w}\)
両辺に \( \bar{x}\) かけると
\((w_1+w_2+\cdots +w_n)\bar{x}=n\bar{w}\bar{x}\) ・・・②
これはデータの分析に混ぜた式処理問題です。
共分散の分子はこれで求められるということをいいたいのでしょうか?
\((x_1-\bar{x})(w_1-\bar{w})+(x_2-\bar{x})(w_2-\bar{w})+\cdots +(x_n-\bar{x})(w_n-\bar{w})\\ \\
= (x_1w_1-x_1\bar{w}-\bar{x}w_1+\bar{x}\bar{w})\\
+(x_2w_2-x_2\bar{w}-\bar{x}w_2+\bar{x}\bar{w})\\
+\cdots \\
+(x_nw_n-x_n\bar{w}-\bar{x}w_n+\bar{x}\bar{w})\\ \\
= (x_1w_1+x_2w_2+\cdots +x_nw_n)\\
-(\color{red}{x_1+x_2+\cdots +x_n})\bar{w}\\
-(\color{blue}{w_1+w_2+\cdots +w_n})\bar{x}\\
+n\bar{x}\bar{w}\\ \\
= (x_1w_1+x_2w_2+\cdots +x_nw_n)\\
-\color{red}{n\bar{x}}\bar{w}\\ \\
-\color{blue}{n\bar{w}}\bar{x}\\ \\
+n\bar{x}\bar{w}\\
= (x_1w_1+x_2w_2+\cdots +x_nw_n)-n\bar{x}\bar{w}\)
ソ:②
展開する前、
すべての項に \( \bar{x}\) と \( \bar{w}\) がついているので、
展開しても展開した数だけついてきます。
だから \( \bar{x}\) と \( \bar{w}\) の項をまとめるとうまく処理できますよ。
続いて第3問へ
⇒ センター試験過去問2018年度数学ⅠA第3問(確率)の解答と解説
第1問を見ていない人は
⇒ センター試験過去問 2018年(平成30年)度数学ⅠAの解答と解説
変わった解答なので少しでも参考になれると良いのですが。
