「データの分析」「活用」は中学の数学データ(中学数学では「資料」)の整理から通じています。しかし、他の分野と切り離しても問題がないくらいなので単独項目として攻略できます。たまに、確率と融合されることもありますが、確率が必要な項目は「統計」に分類されるので、実質的には別物と考えていいでしょう。ただし、単独の項目だからこそ、基本用語を覚えているかどうかで得点の差が大きく出ます。
データの活用分野は満点か0点か
何故なら、問題解決への糸口が限られる、覚えて使うしかない、という限定項目だからです。
他の分野なら、見方を変えれば違った解法が使える場合も多いですが、
このデータの活用は、定義、定理を覚えて使えなければ全くの0点ということもあり得るのです。
そこで、この分野で最低限必要な用語と求め方をまとめておきますので、参考にして下さい。
問題のレベルは電卓を使わなくても答えが出せる「基礎」に限って説明しますのでしっかり反復して下さいね。(反復しないと忘れますよ。)
では、まずは中学の復習から入りましょう。
代表値は3つ
代表値には3つありました。
平均値(アベレージ)、
中央値(メジアン)、
最頻値(モード)
の3つです。
平均値は、データの総和を度数計で割ったものです。
\( \bar x=\displaystyle \frac{x_1+x_2+\cdots +x_n}{n}\)
中央値は、データを小さい順に並べた時の中央に来る値です。
値の中央でなく、度数の中央だということに注意しましょう。
\( x_1,x_2,x_3,x_4,x_5 が小さい順に並んでいるときは x_3\)
データの数が偶数の時は中央2つの平均となることは中学の資料の整理で確認しなおしておいて下さいね。
⇒ 代表値とは?度数分布表の平均値,中央値の求め方と最頻値の答え方
最頻値(「さいひんち」と読むのですよ。)は出てくる割合(頻度)が最も多い値です。
例えば、数学の小テストの結果
5,7,8,5,9,6,8,8,4,3
の10人の得点がデータ(資料)としてあるとします。
※データがあれば、表計算ソフトを使わず手計算の時(入試など)は小さい順に並べるというのはまず最初にやっておくと後々使えます。
ここでは、
3,4,5,5,6,7,8,8,8,9
\(\color{red}{ 平均(アベレージ):(データの総和)\div(データの総度数)} \)
(この場合10人なので10)
\(\displaystyle \frac{3+4+5+5+6+7+8+8+8+9}{10}=6.3\) 点
中央値(メジアン):データを小さい順に並べた時の真ん中にあるデータの値です。
ただし、データの数が偶数の時は真ん中が存在しません。
だから、真ん中の両隣の平均を中央値とします。
ここでは、10人なので5人目と6人目が中央となります。(5人目としないように!)
3,4,5,5,6,|中央|7,8,8,8,9
だからこの場合の中央値は、中央の両隣6,7の平均、6.5 点が中央値となります。
最頻値(モード):度数の最も多い値のことです。
ここでは、8点が3人で度数が一番多いので、最頻値は8 点です。
ここまでは中学の「資料(データ)の整理」にありました。
ここからがデータの分析、活用です。
四分位数
データを小さい方から並べて4等分するだけです。
名前があるので覚えましょう。
データを小さい方から4等分して小さい方から、
第1四分位数 Q 1、
第2四分位数 Q 2 (中央値と一致します)、
第3四分位数 Q 3 と呼びます。
①中央値Q 2
→ ②中央値の左半分のデータの中央値をQ 1
→ ③右半分の中央値をQ 3
の順に印をつければ簡単に出せます。
例えば、上の小テストのデータで見れば、
![]()
これから「箱ひげ図」がかけます。
箱ひげ図の書き方
手順は、
① 最小値、最大値の線を引く。
② Q 1(5),Q 2 (6.5),Q 3(8) で長方形を書く。
③ ひげを書き足す。
それだけです。
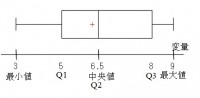
(平均値を「+」で示すこともあります。)
次に、偏差について説明します。
ここは飛ばしても良いですが知っておくと分散が何故2乗されているかが少しはわかります。
何となくですが、それで良いです。
\(\color{red}{ データの1つを代表して x_n として、}\)
\(\color{red}{ データの平均 \bar {x} との差を「偏差」といいます。}\)
\(\color{red}{ つまり、偏差とは x_n- \bar {x} です。}\)
この10個のデータの「偏差の総和」は、
\( (x_1-\bar {x})+(x_2-\bar {x})+\cdots +(x_{10}-\bar {x})\\ \\
=(x_1+x_2+ \cdots +x_{10})-\underline{10\cdot \bar {x}}\) ・・・①
\( \bar {x} は平均だから、\)
\( \bar {x}=\displaystyle \frac{(x_1+x_2+ \cdots +x_{10})}{10}\\ \\
\Leftrightarrow \hspace{10pt} \underline{10\cdot\bar {x}}=(x_1+x_2+ \cdots +x_{10})\)
となっているので、①は
\( (x_1+x_2+ \cdots +x_{10})-(x_1+x_2+ \cdots +x_{10})=0\) ・・・②
となり、偏差の総和ではデータの散らばりが表せないことがわかるでしょう。
だから、というと説明が飛躍しますが、偏差の「2乗の総和」を考えます。
分散と標準偏差
この「偏差の2乗の総和の平均」が、「分散」です。
つまり、
\( 分散 s^2 は \)
分散
\( s^2=\displaystyle \frac{1}{n}\{(x_1-\bar {x})^2+(x_2-\bar {x})^2+\cdots +(x_{10}-\bar {x})^2\}\)
\( (何故「 \color{red}{s^2} 」と表すかは後でわかります。)\)
この分散の正の平方根を「標準偏差」といいます。
\( 分散の s が標準偏差です。\)
標準偏差
\( s=\sqrt{\displaystyle \frac{1}{n}\{(x_1-\bar {x})^2+(x_2-\bar {x})^2+\cdots +(x_{10}-\bar {x})^2\}}\)
他の計算方法もありますが今は用語の確認だけにしておきます。
用語が確認できたら簡単な問題でいいので取り組んでみてください。
抜け落ちているところがはっきりします。
データの活用のポイント
データの活用では難しい計算はほとんどありません。
電卓は試験会場に持ち込めないし、問題作成者もそこまで鬼ではありません。
用語をきちんと覚えているか、
用語の意味を理解しているか、
算出方法は知っているか、
という基本を聞いてくるだけですので、しっかり覚えておくことです。
⇒ データの分析の問題と公式:箱ひげ図の書き方と仮平均の使い方
例題を取り上げて説明しています。
それとH28、29年度と続いて出ている「データの分析」の得点率の低い問題ですが、
中学生でも解ける方法があります。
センターでなら、と限定されますが1つの手段として見ておいてください。
平成30年度の解説は
⇒ センター試験過去問2018年度数学ⅠA第2問(三角比とデータの分析)の解説
この単元、用語を忘れていたらアウトなので、
試験前日にでも確認するといいでしょう。
