直線に対して、与えられたある点と対称な点の座標の求め方です。
日本語でみるとわかりにくいですが、数学の言葉を利用するとすっきりします。
対称とは何対称か、どのような条件をそろえて求めればいいのか、基本的なことをしっかりやれば、難しいことではありません。
座標がわかるときの対称点と直線の位置関係
点や直線が与えられた場合、
問題を解くとき真っ先にやることは位置関係をつかむための図を書くことです。
三角比や幾何ではもちろん、ベクトルや座標上に示せる点や直線や円の場合も簡単なものでもいいので書き出すことで解答の選択肢は増えますよ。
直線 \( y=x-1\) に関して点 \( (1\,,\,2)\) と対称な点の座標 \( (a\,,\,b)\) を求めよ。
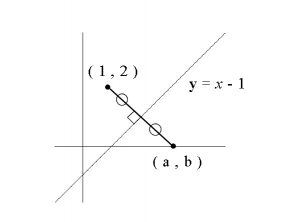
これくらいわかりやすい関数と点だと図を書くことで答の推測もできます。
もちろんそれを答にするのでは無く、出てきた答えがそれに近いかを確認するために利用します。
座標を用いたグラフとともに図を書いて、必要な条件を集めましょう。
数学で「対称」と言えば「線対称」を意味することは中学の数学で学んでいると思いますが、
ここで必要な条件は2つあります。
図を書くと分かりやすいけど、
問題文だけを見ているとなかなか出てきませんよ。
・直線 \( y=x-1\) と 点 \( (1\,,\,2)\) と点 \((a\,,\,b)\) を結ぶ線分が直交する。
・2点 \( (1\,,\,2)\,,\,(a\,,\,b)\) の中点Mは直線 \( y=x-1\) 上にある。
これらは \( y=x-1\) が2点を結ぶ線分の『垂直二等分線』だということです。
この2つを満たせばいいわけですが方法はいくつもありますので、自分で知っていることを書き出せば良いのです。
例えば、出てきた直交条件や中点の座標を利用する方法でも出ますし、
「ベクトル」や「点と直線の距離の公式」を頭に浮かべたならそれを利用してもいいです。
「これじゃないといけない」ということはありません。
少し試して計算が楽に終わりそうなものを利用すれば良いだけです。
中点Mを出して見ましょう。
中点の座標
中点は2点を1:1に内分するのと同じなので、
\( M\left(\displaystyle \frac{1+a}{2}\,,\,\displaystyle \frac{2+b}{2}\right)\)
これが \( y=x-1\) 上にあることから、1つ関係式が出来ます。
点Mを \(y=x-1\) に代入すると、
\( \displaystyle \frac{2+b}{2}=\displaystyle \frac{1+a}{2}-1\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2+b=1+a-2\)
より
\( b=a-3 ・・・①\)
傾きの関係式を出して見ましょう。
2点 \( (1\,,\,2)\,,\,(a\,,\,b)\) を通る直線の傾き \(\color{red}{k}\) は、
\( x\) の増分を \( \Delta x\) , \( y\) の増分を \( \Delta y\) とすると
\(\displaystyle \color{red}{k=\frac{\Delta x}{\Delta y}}\)
ここで
\( \Delta \,x=a-1\)
\( \Delta \,y=b-2\)
より、\(\displaystyle k=\frac{b-2}{a-1}\) となります。
\(y=x-1\) の傾きが1であることと、2直線の直交条件から
\( \color{red}{1\times k=-1}\\ \\
\Leftrightarrow \displaystyle 1\times \frac{b-2}{a-1}=-1\\ \\
\Leftrightarrow \displaystyle \frac{b-2}{a-1}=-1\\ \\
\Leftrightarrow b-2=1-a\)
よって
\( b=-a+3 ・・・②\)
①②から \( (a\,,\,b)=\underline{(3\,,\,0)}\) と簡単に求まります。
直交条件だけ書き出して、いきなり計算に入るより図を書いた方が条件は抜き出しやすくないですか?
垂直に二等分する条件
解き方は他にもあります。
例えば、
\( y=x-1\) が「垂直二等分線」であるということは、
「直線上の点と2点との距離はつねに等しい」ことが言えます。
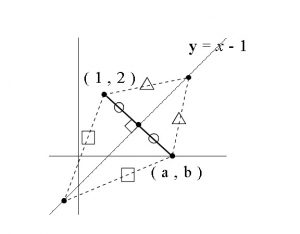
2点間の距離は計算をややこしくするので別の解き方を考えると、ベクトルがあります。
直線の方向ベクトルは \( (1\,,\,1)\) です。
2点をそれぞれ、\( A(1\,,\,2)\,,\,B(a\,,\,b)\) とすると
\( \overrightarrow {AB}=\overrightarrow{OB}-\overrightarrow{OA}=(a-1\,,\,b-2)\)
直交することから内積が0なので
\(1\cdot (a-1)+1\cdot (b-2)=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} a+b=3 ・・・③\)
これは②として出てきた傾きの垂直条件の関係式と同じです。
1つの問題に1つの解法しか存在しないというのは少なくて、
それぞれの問題にいろいろな解法があります。
解法が1つでも多く見つかれば、わからない問題が減るでしょう。
図を書くことで可能になります、
引き出しを多くして答を導く可能性を高めるには
全体を見ながら忘れないように復習することです。