三角関数の合成は最大値や最小値を求める問題の解き方の1つです。三角方程式に使うだけではありません。
三角比では2次関数に置きかえて解くことが多かった最大、最小ですが、
三角関数では2次関数に変形するか、合成を利用することになります。
合成のしかたを復習しながら問題を見ておきましょう。
合成のしかたは後で説明します。
先ずは問題を見ておきましょう。
三角関数の最大値最小値問題を解くときの方針
\( 0≦ x ≦\pi\) とする。
\( y=\sin x+\cos x\)
の最大値および最小値を求めよ。そのときの \( x\) の値も求めよ。
\( \sin x\) と \( \cos x\) が混じっているときは、
どちらかに統一することが三角関数の最大値、最小値を求めるときの方針としておくと良いです。
\( \sin x\,,\,\cos x\) のどちらかが2次になっている場合は、
\( \sin^2\theta+\cos^2\theta=1\) が使えたのですがここでは両方1次なので使えません。
こんなときは「合成」します。
三角関数の合成
合成の仕方、というか方法は人それぞれですが結果は、
\( a\sin\theta+b\cos\theta=r\sin(\theta+\alpha)\)
\( (r=\sqrt{a^2+b^2})\)
\( \alpha\) は \(\displaystyle \cos\alpha =\frac{a}{r} , \sin\alpha=\frac{b}{r}\) を満たす値。
となります。
詳しくは
この \(\alpha\) をどうやって決めるかというと、
加法定理
\( \sin(\theta+\alpha)=\sin\theta\cos\alpha+\sin\alpha\cos\theta\)
を利用します。
\(\sin\theta+\cos\theta\) の場合
\( a=1\,,\,b=1\) より \( r=\sqrt{2}\) なので
\( \sin\theta+\cos\theta=\sqrt{2}(\sin\theta\cdot\displaystyle \frac{1}{\sqrt{2}}+\cos\theta\cdot\displaystyle \frac{1}{\sqrt{2}})\)
と変形できて、
\(\displaystyle \cos\alpha=\frac{1}{\sqrt{2}} , \sin\alpha=\frac{1}{\sqrt{2}}\)
となる \( \alpha\) を条件の範囲内で決めれば良いだけです。
\( \sin\alpha\,,\,\cos\alpha\) とも「正」なので
\( \alpha\) は第1象限の角で \(\displaystyle\alpha=\frac{\pi}{4}\) です。
よって、
\( y=\sin x+\cos x\\ \\
\displaystyle=\sqrt{2}\sin\left(\color{red}{x+\frac{\pi}{4}}\right)\)
定義域は \( 0≦ x ≦\pi\) から
\(\displaystyle \frac{\pi}{4}≦ \color{red}{x+\frac{\pi}{4}}≦ \frac{5\pi}{4}\)
これは半径 \( \sqrt{2}\) の円の一部となります。
単位円で見ると
\(\displaystyle \frac{\pi}{4}≦ x+\frac{\pi}{4}≦ \frac{5\pi}{4}\) において
\(\displaystyle \color{red}{-\frac{1}{\sqrt{2}}≦ \sin\left(x+\frac{\pi}{4}\right)≦ 1}\)
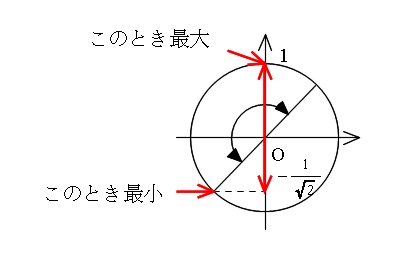
なので \(\displaystyle\color{red}{\sin\left(x+\frac{\pi}{4}\right)}\) を \(\sqrt{2}\) 倍した
\(\displaystyle y=\sin x+\cos x=\sqrt{2}\,\color{red}{\sin\left(x+\frac{\pi}{4}\right)}\)
の値域( \( y\) の変域)は、
\( -1≦ y≦ \sqrt{2}\)
よって、
最小値は \(\displaystyle x+\frac{\pi}{4}=\frac{5\pi}{4}\) のとき \( -1\) ,
最大値は \(\displaystyle x+\frac{\pi}{4}=\frac{\pi}{2}\) のとき \( \sqrt{2}\)。
つまり
\( x=\pi\) のとき最小値 \(-1\)
\(\displaystyle x=\frac{\pi}{4}\) のとき最大値 \(\sqrt{2}\)
三角関数の最大最小を求めるときのポイント
定義域が変わるときは定義域を書き直すこと。
単位円で定義域と値域を書き出すこと。
これらをやっておけば最大値最小値は見えやすくなります。
逆に、単位円を書かずに最小値最大値は出ない、といっておきます。
グラフを使って最大値最小値を出すこともできますが、
グラフを苦手にしている人が多いので単位円を書くことをおすすめしておきます。
(円の半径を問題に合わせて変えても良いです。)
自分で書くのですよ。
もう一つ同じような問題ですがやっておきましょう。
\( 0≦ x ≦ \pi\) とするとき
\( y=\sqrt{3}\sin x-\cos x\)
の最大値,最小値を求めよ。
正弦か余弦に統一するため合成します。
\(y=\sqrt{3}\sin x-\cos x\\ \\
\displaystyle=2\left(\sin x\cdot\frac{\sqrt{3}}{2}-\cos x\cdot \frac{1}{2}\right)\\ \\
\displaystyle=2\sin\left(\color{red}{x-\frac{\pi}{6}}\right)\)
ここで定義域を見てみると
\( 0≦ x ≦ \pi\) なので
\(\displaystyle -\frac{\pi}{6}≦\color{red}{ x-\frac{\pi}{6}}≦ \frac{5\pi}{6}\)
この値域を半径2の円で見てみると、
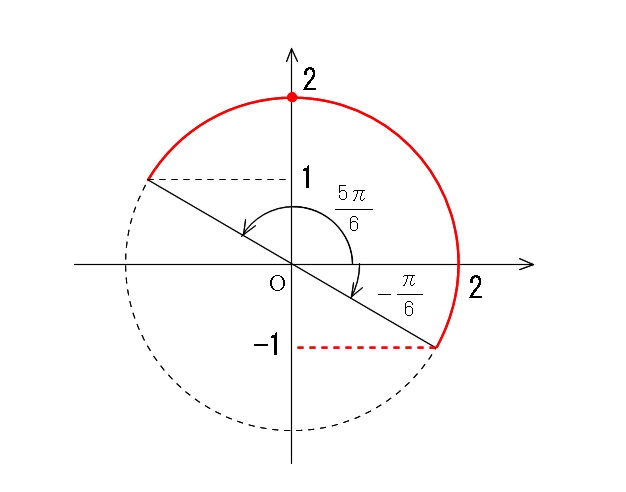
よって、
\(\displaystyle x-\frac{\pi}{6}=\frac{\pi}{2}\) のとき最大となり、
\(\displaystyle x-\frac{\pi}{6}=-\frac{\pi}{6}\) のとき最小となる。
つまり
\(\displaystyle x=\frac{2\pi}{3}\) のとき 最大値 \( 2\)
\( x=0\) のとき最小値 \( -1\)
となります。
三角関数の最大・最小問題は、
必ずではありませんが、「2次関数への誘導」か、この「合成」と言って良いくらいです。
意味なくできる場合もありますが、加法定理が分かっていないと合成はできません。
加法定理と合成はとことん復習しておきましょう。
もちろん、関数なのでグラフの性質も見ておきましょう。