ベクトルの基本である平行条件と3点が一直線上にある条件を見ておきましょう。
ベクトルというと拒絶反応が、なんて人いませんか?
共通テスト(センター試験)のベクトルで点が取れないという人も安心して下さい。
共通テストのベクトルは、ポイントをいくつかおさえれば割と解きやすいです。
共通テストでのベクトルの配点
共通テストの配点は数学\(\,\mathrm{ⅡB100}\,\)点中ベクトルは\(\,20\,\)点ですが、
機械な作業で得点出来ますので、じっくり読んで、実践してみて下さい。
問題を解くときの基本作業さえしておけば、
他の分野同様1週間で6割、7割取れるようになります。
ベクトルの基礎(平行と3点が一直線上にある条件)
ベクトルの平行条件を例題を交えて説明していきます。
ここは基本なので復習がてら見ておいて下さい。
後につながります。
\( ベクトル \vec{a}=(x,-1) , \vec{b}=(2,-3) に対し、\\
\vec{a}+3\vec{b} と \vec{b}-\vec{a} が平行になるように実数 x の値を定めよ。\)
「2つのベクトルが平行になる」
元々ベクトルは方向性を持っています。
だから平行になるということは、
始点をそろえて、一方が他の実数倍になれば良い、と言うことです。
3点\(\,\mathrm{A,B,P}\,\)が一直線上にあるという問題も、
始点を同じにすれば、
「平行」と同じ条件になりますので、確認しておいて下さい。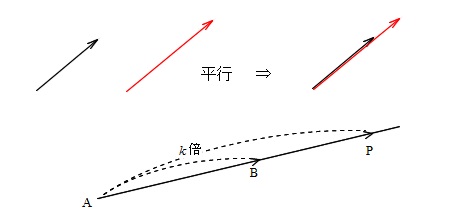
だから平行になる条件としては、
\( 実数 \color{red}{k} を用いて \vec{a}+3 \vec{b}=\color{red}{ k}( \vec{b}- \vec{a})\)
となればいいのです。
\(\hspace{10pt} \vec{a}+3 \vec{b}\\
= (x,-1)+3(2,-3)\\
= (x+6,-10)\)
と
\(\hspace{10pt} \vec{b}- \vec{a} \\
= (2,-3)-(x,-1)\\
= (2-x,-2)\)
とから
\(\hspace{10pt} \vec{a}+3 \vec{b}=\color{red}{ k}( \vec{b}- \vec{a})\)
というのは、
\( \color{blue}{\,x\,成分}\)も\(\color{green}{\,y\,成分}\)も\(\,\color{red}{k}\,\)倍になる
ということなので
\(\color{blue}{\,x\,成分}\) : \(\,x+6 = \color{red}{ k}(2-x)\)
かつ
\(\color{green}{\,y\,成分}\) : \(-10 = \color{red}{k}(-2)\)
が成り立っています。
\(\,y\,\)成分から\(\,\color{red}{ k = 5}\)
これを\(\,x\,\)成分に代入して、
\(\begin{eqnarray}\displaystyle
x+6 &=& \color{red}{k}\,(2-x)\\
x+6 &=& \color{red}{5}\,(2-x)\\
6x &=& 4\\
x&=&\frac{2}{3}
\end{eqnarray}\)
ここまでの計算は簡単な1次方程式です。
人の計算を見ただけで、
自分で計算した気になっている人がいますが、
自分で確認することで力になるんですよ。
問題集に取り組むときでも、
一度で良いから自分で結果まで計算してみましょう。
※
ベクトルが\(\, (\,x\,,\,y\,) \,\)成分で与えられたときは、未定の文字2つまで使えます。
(空間ベクトルだと\(\, (\,x\,,\,y\,,z\,) \,\)となるので文字3つまでです。)
縦ベクトル
ちょっと紙面をとってしまいますが、
ベクトルの成分表示は
「縦ベクトル」
で表示すると計算ミスも少なく、早いですよ。
(普通の表し方は「横ベクトル」といいます。)
例題では、
\( \begin{eqnarray}\vec{a}+3 \vec{b}&=& \left( \begin{array}{c} x \\ -1 \end
{array} \right) + 3 \left( \begin{array}{c} 2 \\ -3 \end
{array} \right)\\
&=& \left( \begin{array}{c} x+6 \\ -10 \end{array} \right)
\end{eqnarray}\)
のようになります。
上段(第1行)と下段(第2行)を横にサッと目を通せるので楽でしょう?
空間になるとさらに計算ミスは減りますし、
計算速度は変わらなくても結果までは早くなります。
あまり変わりないと思うかもしれませんが、
空間ベクトルを扱うときなど非常に便利です。
初めのうちは違和感があるかもしれません。
でも数回使ってみればすぐに慣れますので使ってみて下さい。
これは教科書にもあることだから学校の先生も文句言わないと思います。w
共通テストで、特に\(\,\mathrm{ⅡB}\,\)では時間との勝負になりますから
素早く処理できる方法というのは自分なりに持っておいた方が良いです。
もう一つの特別な解き方
それともう一つ、この問題では基本通りに「実数倍」を平行条件としましたが、
同一直線上の3点で結ばれた図形のつくる面積は0、
ということを利用すると簡単に答が出せる方法もあります。
これは一般的ではないかもしれないので読み飛ばしても良いですよ。
カード『超え太郎』の中に、
「原点と他の2点で作る三角形の面積」
を求める公式があったのを覚えていますか?
あの公式はベクトルの中から出てくるものです。
(教科書『ベクトル』のどこかにあります。たぶん。)
そして、
『平行』であるなら面積は 0 です。
\( ( ad\,-\,bc = 0 )\)
よって
\(\hspace{10pt}(x+6)(-2)-(-10)(2-x) = 0\)
を解いても同じ結果が出ます。
単に中学生でも、ベクトルを知らなくても解ける、というだけですから気にしなくて良いです。
ただ、この場合は簡単すぎて大した差にはなりませんが、共通テストや本試験ではもっと複雑な計算になることもあります。
使えるものは使って良いんですから武器として使いましょう。
こういうところで時間を稼ぐことを繰り返すことで数学\(\,\mathrm{ⅡB}\,\)の時間不足、
随分解消されて楽になってきますよ。
次は「ベクトル基礎編(最小値)」についてお伝えしようと思います。
これは知っておくと考えることが確実に減ります。
試験では一つひとつは聞いてきません。
なのでベクトルの基本はすべて抑えてから練習問題に取り組んだ方が効果的です。
