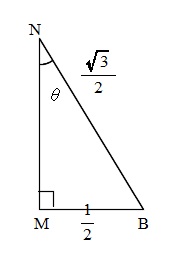ベクトルの内積問題で、センター試験でも出題の割合が多い空間(立体)の図示は条件によっては難しい場合があります。
はっきり見とれる図は書けないでしょうからある程度の位置関係がつかめたら、
図に頼らない、というのが空間図形攻略の1つになります。
空間図形の問題を考えるコツ
空間図形でのコツはいろいろな場面でいっていることなのですが、
「平面を抜き出して」図示すること。
この点については、問題の中で見ることにして先に進みます。
先ずは問題をあげておきます。
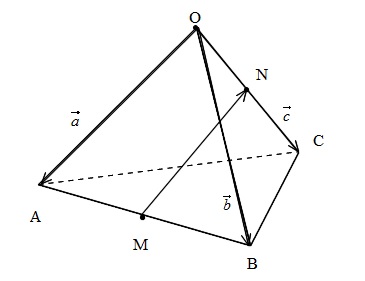
1辺の長さが1の正四面体OABCにおいて、2辺AB,OCの中点をそれぞれ、M,Nとする。
\(\overrightarrow{OA} = \vec{a} , \overrightarrow{OB}= \vec{b} , \overrightarrow{OC}= \vec{c} \)
とする。(続く)
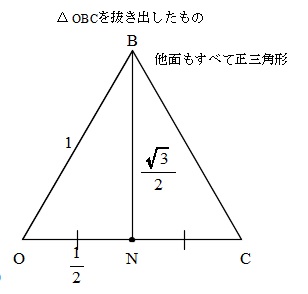
「正四面体」 ⇒ 「すべての面が正三角形」
です。位置関係だけでも図示してみましょう
この図は大まかな位置関係を見るだけにとどめておきます。
立体は平面の組合せで成り立つということに着目して、
平面で考えた方が考えやすいです。
空間ベクトルでも始点は1つに
問題に入ります。
問題(1)
\(\displaystyle \overrightarrow{MN}\, =\, \frac{1}{2} (\, \vec{c}\, -\, \vec{a}\, -\, \vec{b} )\)
を示せ。
(1)平面を抜き出すとすれば、
△OMNですが必要無いでしょう。
当然、始点は1つにしますが「O」が始点ですね。
\(\overrightarrow{MN}\, = \overrightarrow{OM}\,-\,\overrightarrow{ON} \)
\(\displaystyle \overrightarrow{OM} \,= \frac{\vec{a}\,+\,\vec{b}}{2}\)
\(\displaystyle \overrightarrow{ON} \,= \frac{\vec{c}}{2} \)
より
\(\displaystyle \overrightarrow{MN} \,=\frac{\vec{c}\,-\,\vec{a}\,-\,\vec{b}}{2}\,=\frac{1}{2}(\,\vec{c}\,-\,\vec{a}\,-\,\vec{b}\,)\) ・・・①
ここまでは教科書通りで大丈夫ですよね。
問題(2)
\(\overrightarrow{MN}\) と \(\overrightarrow{BN}\)
の内積を求めよ。
(1)はおまけですが、次につながるように誘導されるはずだから使いこなしましょう。
「 \( \overrightarrow{MN}\) と \(\overrightarrow{BM}\) の内積」
つまり
\(|\,\overrightarrow{MN}\,|・|\,\overrightarrow{BM}\,|\cos\angle BNM \)
ですが、 \( \angle BNM \) および \( \cos\angle BNM\) は分かりません。
((3)で分かると言えば分かるのですがまだです。)
そこで、ベクトルの内積をとります。
\( \vec{a}\,,\,\vec{b}\,,\,\vec{c}\) を基底にしているので、
\(\overrightarrow{BN}\) も(1)同様に \( \vec{a}\,,\,\vec{b}\,,\,\vec{c}\) を使って表しましょう。
\(\displaystyle \overrightarrow{BN}\,=\,\overrightarrow{ON}\,-\,\overrightarrow{OB}\\ \\
=\displaystyle \frac{\vec{c}}{2}\,-\,\vec{b}\)
\(=\displaystyle \frac{1}{2} ( \vec{c}\,-\, 2\vec{b}\, )\) ・・・②
①②より
\( \overrightarrow{MN} \cdot \overrightarrow{BN}\\ \\
\displaystyle = \frac{1}{2} ( \,\vec{c}\,-\,\vec{a}\,-\,\vec{b}\,)\cdot \frac{1}{2} ( \vec{c}\,-\,2\vec{b}\,) \\ \\
\displaystyle = \frac{1}{4} ( \,\vec{c}\,-\,\vec{a}\,-\,\vec{b}\,) (\,\vec{c}\,-\,2\vec{b}\,) \\ \\
\displaystyle = \frac{1}{4} ( |\,\vec{c}\,|^2 -2\vec{b}\cdot\vec{c} \,-\,\vec{a}\cdot\vec{c}\,+\,2\vec{a}\cdot\vec{b}\,-\,\vec{b}\cdot\vec{c}\,+\, 2|\,\vec{b}\,|^2 )\)
ここで正四面体の面はすべて1辺の長さが1の正三角形なので
\(\displaystyle \vec{a}\cdot\vec{b}\,=\,\vec{b}\cdot\vec{c}\,=\,\vec{c}\cdot\vec{a}\,=|1|\cdot |1|\cdot\cos\frac{\pi}{3}=\frac{1}{2}\)
なので
\(\overrightarrow{MN} \cdot \overrightarrow{BN}\\ \\
\displaystyle = \frac{1}{4} ( 1 – 1 – \frac{1}{2} + 1 – \frac{1}{2} +2 )\)
\(\displaystyle = \frac{1}{2} \) ・・・③
この内積も問題はないでしょう。
「正四面体」を知らなければ話は別ですが、、、笑
問題(3)
\( \angle MNB=\theta \) とするとき、 \( \cos \theta\) を求めよ。
△BMNを抜き出せば直角三角形なので、
三平方の定理からMNの長さは簡単にでるのですが、
ここではベクトルを使って長さ(大きさ)を出しておきます。
空間ベクトルでも「大きさ」は2乗
ベクトルの大きさを見たら2乗です。
\(\displaystyle |\,\overrightarrow{MN}\,|^2= \frac{1}{4} (\,\vec{c}\,-\,\vec{a}\,-\,\vec{b}\,)^2\)
2乗の部分だけを計算すると
\( (\,\vec{c}\,-\,\vec{a}\,-\,\vec{b}\,)^2\\ \\
=|\,\vec{c}\,|^2\,+\,|\,\vec{a}\,|^2\,+\,|\,\vec{b}\,|^2-2\vec{a}\cdot\vec{c}\,+\,2\vec{a}\cdot\vec{b}\,-\,2\vec{b}\cdot\vec{c}\\ \\
=1+1+1+1-1-1=2\)
となるので、
\(\displaystyle |\,\overrightarrow{MN}\,|^2= \frac{1}{4} \times 2 = \frac{1}{2}\)
これから大きさなので「正の平方根」をとって
\(\displaystyle |\,\overrightarrow{MN}\,|= \frac{1}{\sqrt{2}} \)
がわかります。
\( \displaystyle |\,\overrightarrow{BN}\,|= \frac{\sqrt{3}}{2} \)
は図からわかっているので、
\( \overrightarrow{MN} \cdot \overrightarrow{BN}\\ \\
= |\,\overrightarrow{MN}\,| \cdot |\,\overrightarrow{BN}\,| \cos \theta \\ \\
\displaystyle = \frac{1}{\sqrt{2}}\cdot \frac{\sqrt{3}}{2} \cos \theta \)
③から
\(\displaystyle \cos \theta\,=\frac{\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{6}}{3} \)
とベクトルを使って求めることが出来ます。
まとめ
三角比、平面幾何の知識でも余弦(\(\,\cos\,\))の値は求めることは出来ます。
今回のようにベクトルでも求めることが出来ます。
どっちかでなければならない、ということはありません。
が、
幾何を利用してもベクトルを利用しても求められる。
両方出来る方が良いですよね。
センター試験では誘導があるので
「自分の好きな方で解く」
という選択肢は無いに等しいですが、引き出しは多い方が良いですね。
ここなどは良く問題にされます。
ベクトルの大きさと内積を外すと問題は解けません。