2019年(平成31年)度に行われたセンター試験数学2Ｂ第2問の解説です。
第2問は微分と積分の基本問題ですが文字が多くイメージしにくかったかもしれません。
文字が残ったままの積分になりますが定数なので気にせず進めることがポイントです。
正答はセンターが発表していますので確認してください。
この問題は数学ⅡBの部分のみの問題です。
第\(\,2\,\)問は必答問題です。
(1)
まずは問題にある条件を整理しておきましょう。
曲線\(\,C\,\)：\(\,y=f(x)=x^3+px^2+qx\,\)
\(\,C\,\)は\(\,x=-1\,\)で極値\(\,2\,\)をとる。
曲線\(\,D\,\)：\(\,y=-kx^2\,\)
\(\,D\,\)上の点\(\,(a,-ka^2)\,\)を\(\,A\,\)とする。
\(\,k＞0\,\) , \(\,a＞0\,\)
(1)
関数\(\,f(x)=x^3+px^2+qx\,\)が\(\,x=-1\,\)で極値\(\,2\,\)をとることから
\(\,f'(-1)=\color{black}{\fbox{\(\,\color{red}{ 0 }\,\)}}\,\) , \(\,f(-1)=2\,\)
がいえます。
\(\,f(x)=x^3+px^2+qx\,\)
\(\,f'(x)=3x^2+2px+q\,\)
なので
\(\begin{eqnarray}
f'(-1)&=&3(-1)^2+2p(-1)+q\\
&=&\color{blue}{3-2p+q=0}
\end{eqnarray}\)
また
\(\begin{eqnarray}
f(-1)&=&(-1)^3+p(-1)^2+q(-1)\\
&=&\color{blue}{-1+p-q=2}
\end{eqnarray}\)
これらを連立して
\( \begin{cases}
\hspace{7pt} 3-2p+q=0\\ \\
\hspace{7pt} -1+p-q=2
\end{cases}\)
これを解いて
\(\,p=\color{black}{\fbox{\(\,\color{red}{ 0 }\,\)}}\,\) , \(\,q=\color{black}{\fbox{\(\,\color{red}{ -3 }\,\)}}\,\)
\(\,f'(x)=0\,\)がいえても極値を持つとは限りませんが、
極値を持つなら\(\,f'(x)=0\,\)はいえますよ。
\(\,p,q\,\)が決まったので元に戻しておきましょう。
\(\,f(x)=x^3-3x\,\)
\(\,f'(x)=3x^2-3\,\)
これで文字が減りました。
\(\begin{eqnarray}
f'(x)&=&3x^2-3\\
&=&3(x^2-1)\\
&=&3(x+1)(x-1)=0
\end{eqnarray}\)
から\(\,x=1\,\)のとき
\(\,f(1)=(1)^3-3(1)=-2\,\)
なので
\(\,x=\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}}\,\)のとき極大値\(\color{black}{\fbox{\(\,\color{red}{ -2 }\,\)}}\)をとる。
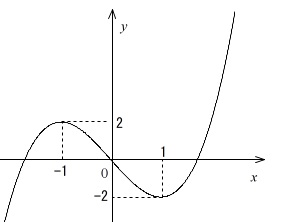
簡単ですが、出てきた定数、実数、を自分でわかり安く書き出していくことがポイントです。
(2)
点\(\,\mathrm{A}\,(\,a\,,\,-ka^2\,)\,\)は\(\,\mathrm{D}\,\)上の点で\(\,x\,\)座標は正の範囲にあります。
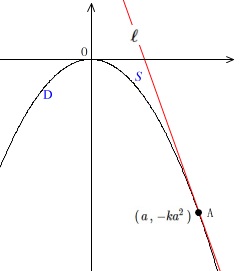ここでは\(\,f(x)\,\)は関係していません。
\(\,y=-kx^2\,\)
\(\,y’=-2kx\,\)
より点\(\,\mathrm{A}\,(\,\color{red}{a}\,,\,\color{blue}{-ka^2}\,)\,\)における接線は、
\(\begin{eqnarray}
y-(\color{blue}{-ka^2})&=&-2ka(x-\color{red}{a})\\
y&=&-2kax+2ka^2-ka^2\\
&=&\color{black}{\fbox{\(\color{red}{ -2 }\)}}kax+ka^\color{black}{\fbox{\(\,\color{red}{2}\,\)}} ･･･①
\end{eqnarray}\)
\(\,\ell\,\)と\(\,x\,\)軸との交点は①において\(\,y=0\,\)と置けば求まります。
\(\begin{eqnarray}\displaystyle
0&=&-2kax+ka^2\\
2kax&=&ka^2\\
x&=&\frac{\color{black}{\fbox{\(\color{red}{ a }\)}}}{\color{black}{\fbox{\(\color{red}{ 2 }\)}}}
\end{eqnarray}\)
\(\,D\,\)と\(\,x\,\)軸(\(\,y=0\,\))と直線\(\,x=a\,\)とで囲まれる図形の面積は
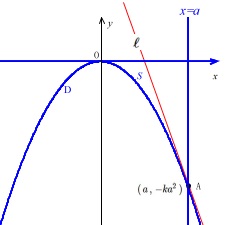積分区間を\(\,[\,0\,,\,a\,]\,\)として
\(\hspace{10pt}\displaystyle \int^{a}_{0}\left\{(0)-(kx^2)\right\}dx\\
\displaystyle =\int^{a}_{0}kx^2 dx\\
\displaystyle =\left[\frac{1}{3}kx^3\right]^a_0\\
\displaystyle =\frac{1}{3}ka^3\\
\displaystyle =\frac{k}{\color{black}{\fbox{\(\,\color{red}{ 3 }\,\)}}}a^\color{black}{\fbox{\(\,\color{red}{3}\,\)}}\)
これから面積\(\,\color{blue}{S}\,\)は
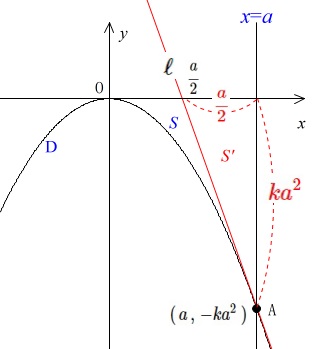直角三角形\(\,\color{red}{S’}\,\)を引けば求めることができます。
\(\begin{eqnarray}\displaystyle
\color{red}{S’}&=&\frac{1}{2}\times \frac{a}{2}\times ka^2\\
&=&\color{red}{\frac{k}{4}a^3}
\end{eqnarray}\)
より
\(\begin{eqnarray}\displaystyle
\color{blue}{S}&=&\frac{k}{3}a^3-\color{red}{S’}\\
&=&\frac{k}{3}a^3-\color{red}{\frac{k}{4}a^3}\\
&=&\frac{4k-3k}{12}a^3\\
&=&\frac{k}{\color{black}{\fbox{\(\,\color{red}{ 12 }\,\)}}}a^\color{black}{\fbox{\(\,3\,\)}}
\end{eqnarray}\)
(3)
ここで再び\(\,C\,\)が登場します。
点\(\,\mathrm{A}\,(\,a\,,\,-ka^2\,)\,\)は\(\,\mathrm{D}\,\)上の点で\(\,x\,\)座標は正の範囲
かつ
点\(\,\mathrm{A}\,(\,a\,,\,-ka^2\,)\,\)は\(\,\mathrm{C}\,\)上の点
かつ
\(\,A\,\)における\(\,D\,\)の接線\(\,\ell\,\)が\(\,C\,\)に接する。
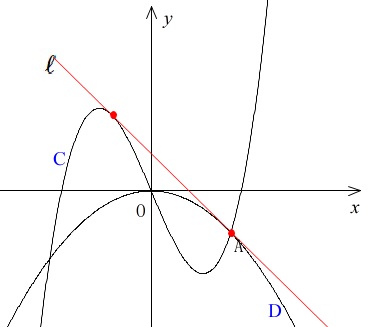接点が同じというわけではありません。
『このとき(2)の\(\,S\,\)の値を求めよう。』
です。『求めよ。』ではなく、誘導してくれます。
『\(\,A\,\)が\(\,C\,\)上にあるので』
\(A\,(\,a\,,\,-ka^2\,)\,\)
を
\(\,f(x)=x^3-3x\,\)
に代入して成り立つということです。
\(\begin{eqnarray} \displaystyle
(-ka^2)&=&(a)^3-3(a)\\
k&=&\frac{a^3-3a}{-a^2}\\
&=&-a+\frac{3}{a}\\
&=&\frac{\color{black}{\fbox{\(\,\color{red}{ 3 }\,\)}}}{\color{black}{\fbox{\(\,\color{red}{ a }\,\)}}}-\color{black}{\fbox{\(\,\color{red}{ a }\,\)}}
\end{eqnarray}\)
\(\,C\,\)と接線\(\,\ell\,\)との接点の\(\,x\,\)座標を\(\,b\,\)とすると
\(\,f(x)=x^3-3x\,\)
\(\,f'(x)=3x^2-3\,\)
より接点は
\(\,(\,b\,,\,b^3-3b\,)\,\)
また
\(\,f'(b)=3b^2-3\,\)
よって接線の方程式は
\(\begin{eqnarray}
y-(b^3-3b)&=&(3b^2-3)(x-b)\\
y&=&(3b^2-3)x-3b^3+3b+(b^3-3b)\\
&=&\color{black}{\fbox{\(\,\color{red}{ 3 }\,\)}}(b^2-\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}})x-\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}b^3 ･･･②
\end{eqnarray}\)
②の右辺を\(\,g(x)\,\)とおくと
\(\,g(x)=3(b^2-1)x-2b^3\,\)
このとき\(\,x=b\,\)は接点の\(\,x\,\)座標なので、
\(\,f(x)-g(x)=0\,\)の重解になることを考慮して
\(\begin{eqnarray}
f(x)-g(x)&=&(x^3-3x)-\{3(b^2-1)x-2b^3\}\\
&=&x^3-3x-3(b^2-1)x+2b^3\\
&=&(x-\color{black}{\fbox{\(\,\color{red}{ b }\,\)}})^2(x+\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}b)
\end{eqnarray}\)
となり接点ではない方の\(\,D\,\)との交点\(\,A\,\)の\(\,x\,\)座標が\(\,x=-2b\,\)となるので
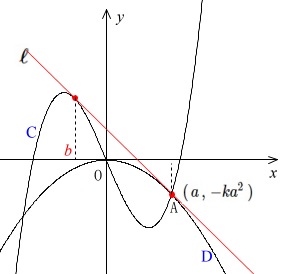
\(\,a=-\color{black}{\fbox{\(\, 2 \,\)}}b\,\)
①と②の直線は同じ直線を表しているので、
\(\,y=\color{red}{-2ka}x\color{blue}{+ka^2}\, ･･･①\)
\(\,y=\color{red}{3(b^2-1)}x\color{blue}{-2b^3}\, ･･･②\)
を比較することで
\( \begin{cases}
\hspace{4pt} \color{red}{-2ka}=\color{red}{3(b^2-1)}\\ \\
\hspace{4pt} \color{blue}{ka^2}=\color{blue}{-2b^3}
\end{cases}\)
ここで \(\,\color{magenta}{a=-2b}\,\) を利用しますが、
もう一つ \(\displaystyle \color{magenta}{k=\frac{3}{a}-a}\,\) もあります。
\(\,a=-2b\,\)として一度\(\,a\,\)を消去するか
\(\displaystyle b=-\frac{1}{2}a\,\)として\(\,b\,\)を消去するか
はどちらでも良いです。
誘導では『傾きを比較することにより』となっているので
\(\begin{eqnarray}\displaystyle
\color{red}{-2ka}&=&\color{red}{3(b^2-1)}\\
-2\times \left(\color{magenta}{\frac{3}{a}-a}\right)\times a&=&3\left\{\left(\color{magenta}{-\frac{1}{2}a}\right)^2-1\right\}\\
-6+2a^2&=&\frac{3}{4}a^2-3\\
-24+8a^2&=&3a^2-12\\
5a^2&=&12\\
a^2&=&\frac{\color{black}{\fbox{\(\,\color{red}{ 12 }\,\)}}}{\color{black}{\fbox{\(\,\color{red}{ 5 }\,\)}}}
\end{eqnarray}\)
出ました。
『したがって』
どこからどこまでしたがうのか確認しましょう。
\(\,S\,\)は(2)で指定された部分です。
(2)から
\(\displaystyle \color{red}{S=\frac{k}{12}a^3}\,\)
(3)の条件では
\(\displaystyle \color{blue}{k}=\frac{3}{a}-a=\color{blue}{\frac{3-a^2}{a}}\)
\(\displaystyle \color{magenta}{a^2}=\color{magenta}{\frac{12}{5}}\,\)
なので
\(\begin{eqnarray}
\color{red}{S}&=&\color{red}{\frac{k}{12}a^3}\\
&=&\frac{1}{12}\times\color{blue}{k} \times a^3\\
&=&\frac{1}{12}\times\color{blue}{\left(\frac{3-a^2}{a}\right)} \times a^3\\
&=&\frac{1}{12}\times (3-a^2)\times a^2\\
&=&\frac{1}{12}\times \left(3-\color{magenta}{\frac{12}{5}}\right)\times \color{magenta}{\frac{12}{5}}\\
&=&\frac{15-12}{5}\times \frac{1}{5}\\
&=&\frac{\color{black}{\fbox{\(\,\color{red}{ 3 }\,\)}}}{\color{black}{\fbox{\(\,\color{red}{ 25 }\,\)}}}
\end{eqnarray}\)
実際に自分の手を動かして計算すれば見た目ほど困難ではありません。
⇒ センター試験数学2Ｂ2019年度選択問題第3問(数列)の解説
第3問は数列ですが、例年通りなので方針は変わりません。
漸化式は解こうと考えない方が良いですね。
式の処理に時間がかかると思われます。
⇒ センター試験数学2Ｂ2019年度第1問(三角関数と指数対数)の解説
第\(1\)問とこの第\(2\)問で時間を稼いでおくことです。
共通テストになっても\(\,ⅡB\,\)の傾向は変わりません。
というより変えようがありません。