2019年(平成31年度)に行われたセンター試験数学2B第1問の解説です。
第1問は三角関数と指数対数の問題で例年と変わりありません。
誘導もしっかりされているので基本をおさえておけば得点しやすいところです。
ⅡBは後半で時間を必要とする問題がひかえていることが多いのでさっさと済ませましょう。
正答はセンターが発表していますので確認してください。
この問題は数学ⅡBの部分のみの問題です。
第1問は必答問題です。
〔1〕三角関数
関数
\(f(\,\theta\,)=3\,\sin^2\theta+4\,\sin \theta\,\cos\theta-\cos^2\theta\)
\(\,\theta\,\)だけしか出てこないので\(\,2\,\)倍角だろうと推測できますが、
誘導に乗ってもいいです。
\(\,2\,\)倍角から始めたいですが、加法定理を知らないと話にならないので確認しておきます。
\(\color{red}{\fbox{ 三角関数の加法定理 }}\)
\(\sin (\color{red}{\alpha}+\color{blue}{\beta})=\sin\color{red}{\alpha}\cos\color{blue}{\beta}+\cos\color{red}{\alpha}\sin\color{blue}{\beta}\)
\(\cos (\color{red}{\alpha}+\color{blue}{\beta})=\cos\color{red}{\alpha}\cos\color{blue}{\beta}-\sin\color{red}{\alpha}\sin\color{blue}{\beta}\)
※
加法定理は確率にもありますので『三角関数の』とつけておきました。
\(\,2\,\)倍角の公式は『加法定理』において
\(\color{red}{\alpha}=\color{blue}{\beta}=\theta\)
とおいて
\(\begin{eqnarray}
\color{red}{\sin 2\theta}&=&\sin(\theta+\theta)\\
&=&\sin\theta\cos\theta+\cos\theta\sin\theta\\
&=&\color{red}{2\sin\theta\cos\theta}
\end{eqnarray}\)
\(\begin{eqnarray}
\color{blue}{\cos 2\theta}&=&\cos(\theta+\theta)\\
&=&\cos\theta\cos\theta-\sin\theta\sin\theta\\
&=&\color{blue}{\cos^2\theta-\sin^2\theta} ・・・\color{red}{①}\\
①&=&\cos^2-(1-\cos^2\theta)\\
&=&\color{blue}{2\cos^2\theta-1} ・・・\color{red}{②}\\
①&=&(1-\sin^2\theta)-\sin^2\theta\\
&=&\color{blue}{1-2\sin^2\theta} ・・・\color{red}{③}
\end{eqnarray}\)
\(\cos\)の\(\,2\,\)倍角は①②③のどれを使うかは問題によって変えればいいです。
\(\,2\,\)倍角の公式を書き出したところで問題に入りましょう。
関数は
\(f(\,\theta\,)=3\,\sin^2\theta+4\,\sin \theta\,\cos\theta-\cos^2\theta\)
です。
(1)
単なる代入問題です。
\(\begin{eqnarray}
f(\,0\,)&=&3\,\sin^2 0+4\,\sin 0\,\cos0-\cos^2 0\\
&=&0+0-1\\
&=&\color{black}{\fbox{\(\,\color{red}{ -1 }\,\)}}
\end{eqnarray}\)
\(\begin{eqnarray}\displaystyle
f(\,\frac{\pi}{3}\,)&=&3\,\left(\sin\frac{\pi}{3}\right)^2+4\,\sin \frac{\pi}{3}\,\cos\frac{\pi}{3}-\left(\cos\frac{\pi}{3}\right)^2\\
&=&3\,\left(\frac{\sqrt{3}}{2}\right)^2+4\times\frac{\sqrt{3}}{2}\times\frac{1}{2}-\left(\frac{1}{2}\right)^2\\
&=&\frac{9}{4}+\sqrt{3}-\frac{1}{4}\\
&=&\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}+\sqrt{\color{black}{\fbox{\(\,\color{red}{ 3 }\,\)}}}
\end{eqnarray}\)
(2)
\(\,2\,\)倍角の公式はすでに書いてあります。
②の形を使えばいいだけです。
\(\begin{eqnarray}\displaystyle
\cos 2\theta&=&2\cos^2\theta-1\\
2\cos^2\theta&=&\cos 2\theta+1\\
\cos^2\theta&=&\frac{\cos 2\theta+\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}}}{\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}}
\end{eqnarray}\)
\(f(\,\theta\,)\)を\(\,2\,\)倍角で表します。
\(f(\,\theta\,)=3\,\color{red}{\sin^2\theta}+4\,\color{blue}{\sin \theta\,\cos\theta}-\color{magenta}{\cos^2\theta}\)
\(\,2\,\)倍角の公式
\(\,\sin 2\theta=2\color{blue}{\sin\theta\cos\theta}\,\)
\(\,\begin{eqnarray}
\cos 2\theta&=&2\color{magenta}{\cos^2\theta}-1 ・・・\color{red}{②}\\
&=&1-2\color{red}{\sin^2\theta} ・・・\color{red}{③}
\end{eqnarray}\,\)
を見比べればすぐに終わります。
\(\,\sin 2\theta=2\color{blue}{\sin\theta\cos\theta}\,\)
から
\(\displaystyle \,\color{blue}{\sin\theta\cos\theta}=\frac{\sin 2\theta}{2}\,\)
\(\,f(\,\theta\,)\,\)の係数から
\(\sin 2\theta=\,2\color{blue}{\sin\theta\cos\theta}\,\)
のままでもいいのですが奇数係数のときにも使える様に変形しておきます。
③から
\(\displaystyle \,\color{red}{\sin^2\theta}=\frac{1-\cos 2\theta}{2}\,\)
②から
\(\displaystyle \,\color{magenta}{\cos^2\theta}=\frac{\cos 2\theta+1}{2}\,\)
これらを\(\,f(\,\theta\,)\,\)に代入します。
\(\begin{eqnarray}\displaystyle
f(\,\theta\,)&=&3\,\color{red}{\sin^2\theta}+4\,\color{blue}{\sin \theta\,\cos\theta}-\color{magenta}{\cos^2\theta}\\
&=&3\times \left(\frac{1-\cos 2\theta}{2}\right)+4\times \left(\frac{\sin 2\theta}{2}\right)-\left(\frac{\cos 2\theta+1}{2}\right)\\
&=&\frac{3}{2}-\frac{3}{2}\cos2\theta+2\sin\theta-\frac{\cos2\theta}{2}-\frac{1}{2}\\
&=&\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}\sin2\theta-\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}\cos2\theta+\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}}
\end{eqnarray}\)
なんだか機械的で面白くないのですが、考えることないです。
(3)
加法定理、倍角が出てきたら次は合成ですね。
問題は
『最大の整数の値\(\,m\,\)とそのときの\(\,\theta\,\)の値を求めよ。』
ではありません。
『最大の整数の値\(\,m\,\)とそのときの\(\,\theta\,\)の値を(誘導にしたがって)求めよう。』
です。
この『求めよう。』は、誘導してくれる合図ですよ。
\(\,f(\,\theta\,)=\color{red}{2}\sin2\theta-\color{blue}{2}\cos2\theta+1\, ・・・①\)
※
\(\,①\,\)と倍角の\(\,\color{red}{①}\,\)は違いますので注意してください。
倍角の\(\,\color{red}{①}\,\)は私が勝手につけた式番です。
①を合成します。
\(\sqrt{\color{red}{2}^2+\color{blue}{2}^2}=\sqrt{8}=2\sqrt{2}\)
から
\(\begin{eqnarray}
f(\,\theta\,)&=&\color{red}{2}\sin\theta-\color{blue}{2}\cos\theta+1\\
&=&2\sqrt{2}\left( \underline{\sin\theta\times \frac{1}{\sqrt{2}}-\cos\theta\times \frac{1}{\sqrt{2}}} \right)+1
\end{eqnarray}\)
下線部を加法定理にあてはめて
\(\begin{eqnarray}
f(\,\theta\,)&=&2\sqrt{2}\left( \underline{\sin 2\theta\times \frac{1}{\sqrt{2}}-\cos2\theta\times \frac{1}{\sqrt{2}}} \right)+1\\
&=&2\sqrt{2}\left( \underline{\sin2\theta\times \cos\frac{\pi}{4}-\cos2\theta\times \sin\frac{\pi}{4}} \right)+1\\
&=&\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}\sqrt{\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}}\,\underline{\sin\left(2\theta-\frac{\pi}{\color{black}{\fbox{\(\,\color{red}{ 4 }\,\)}}}\right)}+\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}}
\end{eqnarray}\)
と変形できて
\(\,0≦\theta≦\pi\,\)
のとき
\(\,0≦\color{red}{2}\theta≦\color{red}{2}\pi\,\)
さらに
\(\displaystyle 0\color{blue}{-\frac{\pi}{4}}≦2\theta\color{blue}{-\frac{\pi}{4}}≦2\pi-\color{blue}{\frac{\pi}{4}}\\
\Leftrightarrow \displaystyle -\frac{\pi}{4}≦2\theta-\frac{\pi}{4}≦\frac{7\pi}{4}\)
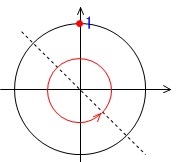
\(\displaystyle 2\theta-\frac{\pi}{4}=\frac{\pi}{2}\)となるとき\(\displaystyle \sin\left(2\theta-\frac{\pi}{4}\right)\)は最大で\(\,1\,\)、
このとき
\(\begin{eqnarray}
f(\theta)&=&2\sqrt{2}\times +1\\
&=&3.8\cdots
\end{eqnarray}\)
最大の整数は\(\,m=\color{black}{\fbox{\(\,\color{red}{ 3 }\,\)}}\,\)
また \(\,f(\theta)=3\,\) となるとき
\(\begin{eqnarray}\displaystyle
2\sqrt{2}\sin\left(2\theta-\frac{\pi}{4}\right)+1&=&3\\
\sin\left(\color{red}{2\theta}\color{blue}{-\frac{\pi}{4}}\right)&=&\frac{1}{\sqrt{2}}\\
\end{eqnarray}\)
これを満たすのは
\(\begin{eqnarray}\displaystyle
\color{red}{2\theta}\color{blue}{-\frac{\pi}{4}}&=&\frac{\pi}{4}\,,\,\frac{3\pi}{4}\\
2\theta&=&\frac{\pi}{4}\color{blue}{+\frac{\pi}{4}}\,,\,\frac{3\pi}{4}\color{blue}{+\frac{\pi}{4}}\\
2\theta&=&\frac{\pi}{2}\,,\,\pi\\
\theta&=&\frac{\pi}{\color{black}{\fbox{\(\,\color{red}{ 4 }\,\)}}}\,,\,\frac{\pi}{\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}}
\end{eqnarray}\)
次に行きいます。
〔2〕指数対数
連立方程式
\( \begin{cases}
\hspace{7pt} \log_2(x+2)-2\log_4(y+3)=-1 ・・・②\\ \\
\displaystyle \hspace{7pt} \left(\frac{\,1\,}{\,3\,}\right)^y-11\left(\frac{\,1\,}{\,3\,}\right)^{x+1}+6=0 ・・・③
\end{cases}\)
を満たす実数\(\,x,y\,\)を『求めよう。』です。
誘導に乗るんですよ。
ただし、『対数を見たら?』
真数条件を出す
底をそろえる
これは先ずやっておくことです。
⇒ 対数の計算公式一覧(底の変換と真数の掛け算・割り算の変形のしかた)
ところがこの問題はそれも誘導してくれています。
真数条件より、
\(\,x+2>0\,\) から \(\,x\,>\color{black}{\fbox{\(\color{red}{ -2 }\)}}\,\)
\(\,y+3>0\,\) から \(\,y\,>\color{black}{\fbox{\(\color{red}{ -3 }\)}}\,\)
底を\(\,2\,\)にそろえます。
問題によって違いますが、底をそろえるときはできるだけ小さい素数でそろえるといいです。
\(\displaystyle \log_\color{red}{a}\color{blue}{b}=\frac{\log_c\color{blue}{b}}{\log_c\color{red}{a}}\,\)
なので
\(\begin{eqnarray}\displaystyle
\log_\color{red}{4}\color{blue}{(y+3)}&=&\frac{\log_2\color{blue}{(y+3)}}{\log_2\color{red}{4}}\\
&=&\frac{\log_2(y+3)}{\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}}
\end{eqnarray}\)
これを②にあてはめると
\(\begin{eqnarray}
\log_2(x+2)-2\color{red}{\log_4(y+3)}&=&-1\\
\log_2(x+2)-2\times \color{red}{\frac{\log_2(y+3)}{2}}&=&-1\\
\log_2(x+2)-\log_2(y+3)&=&-1
\end{eqnarray}\)
両辺入れかえて整理すると
\(\begin{eqnarray}
\log_2(y+3)&=&\log_2(x+3)+1\\
&=&\log_2(x+3)+\log_22\\
&=&\log_22(x+3)
\end{eqnarray}\)
底は同じなので真数どうしが等しくなるので
\(\begin{eqnarray}
y+3&=&2(x+2)\\
y&=&2x+4-3\\
y&=&\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}x+\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}} ・・・④
\end{eqnarray}\)
ここまでは誘導なしでも進むでしょう。
次は③を変形します。
\(\displaystyle \left(\frac{\,1\,}{\,3\,}\right)^y-11\left(\frac{\,1\,}{\,3\,}\right)^{x+1}+6=0 ・・・③\,\)
において \(\displaystyle t=\left(\frac{1}{3}\right)^x\,\) とおくと、、、
本当は置換した時点で定義域の変換をしておくべきなのですが、後で問題になっていました。
ただ、\(\,y\,\)は消去しておきたいですね。
④より\(\,y=2x+1\,\)なので③は
\(\begin{eqnarray}\displaystyle
\left(\frac{\,1\,}{\,3\,}\right)^y-11\left(\frac{\,1\,}{\,3\,}\right)^{x+1}+6&=&0\\
\left(\frac{\,1\,}{\,3\,}\right)^{(2x+1)}-11\left(\frac{\,1\,}{\,3\,}\right)^{x+1}+6&=&0\\
\frac{1}{3} \left(\frac{\,1\,}{\,3\,}\right)^{2x}-11\cdot \frac{1}{3} \left(\frac{\,1\,}{\,3\,}\right)^{x}+6&=&0
\end{eqnarray}\)
ここで \(\displaystyle t=\left(\frac{1}{3}\right)^x\,\) とおくと
\(\displaystyle \left(\frac{\,1\,}{\,3\,}\right)^{2x}=t^2\,\)
なので
\(\begin{eqnarray}\displaystyle
\frac{1}{3}t^2-\frac{11}{3}t+6&=&0\\
t^2-\color{black}{\fbox{\(\,\color{red}{ 11 }\,\)}}t+\color{black}{\fbox{\(\,\color{red}{ 18 }\,\)}}&=&0 ・・・⑤
\end{eqnarray}\)
ところで
\(\displaystyle t=\left(\frac{1}{3}\right)^x\,\)
とすると \(\,x>-2\,\) なので
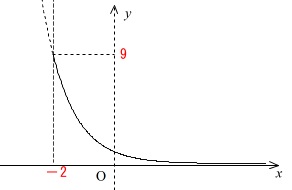
\(\,\color{black}{\fbox{\(\,\color{red}{ 0 }\,\)}}\,<\,t\,<\,\color{black}{\fbox{\(\,\color{red}{ 9 }\,\)}}\, ・・・⑥\)
⑤を解くと
\(\begin{eqnarray}
t^2-11t+18&=&0\\
(t-2)(t-9)&=&0\\
t&=&2\,,\,9
\end{eqnarray}\)
⑥の \(\,0<t<9\,\) を満たすのは
\(\,t=\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}\,\)
元に戻します。
\(\displaystyle \,t=\left(\,\frac{1}{3}\,\right)^x\,\)
と置いていたので
\(\begin{eqnarray}
\left(\,\frac{1}{3}\,\right)^x&=&2\\
\end{eqnarray}\)
対数の定義に戻ってもいいのですが、底を\(\,3\,\)にして両辺の対数を取りましょう。
\(\begin{eqnarray}\displaystyle
\left(\,\frac{1}{3}\,\right)^x&=&2\\
\log_3\left(\,\frac{1}{3}\,\right)^x&=&\log_32\\
\log_3(3^{-1})^x&=&\log_32\\
\log_33^{-x}&=&\log_32\\
-x&=&\log_32\\
x&=&-\log_32\\
&=&\log_3(2)^{-1}\\
&=&\log_3\frac{\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}}}{\color{black}{\fbox{\(\,\color{red}{ 2 }\,\)}}}
\end{eqnarray}\)
このとき \(\,y=2x+1\,\) なので
\(\begin{eqnarray}\displaystyle
y&=&2x+1\\
&=&2\left(\log_3\frac{1}{2}\right)+\log_33\\
&=&\log_3\left(\frac{1}{2}\right)^2+\log_33\\
&=&\log_3\left\{\left(\frac{1}{4}\right)\times 3\right\}\\
&=&\log_3\frac{\color{black}{\fbox{\(\,\color{red}{ 3 }\,\)}}}{\color{black}{\fbox{\(\,\color{red}{ 4 }\,\)}}}
\end{eqnarray}\)
\(\displaystyle \left(\,\frac{1}{3}\,\right)^x=2\,\)
を定義に戻って底の変換すると
\(\begin{eqnarray}\displaystyle
x&=&\log_{\frac{1}{3}}2\\
&=&\frac{\log_32}{\log_3{\frac{1}{3}}}
&=&\frac{\log_32}{\log_33^{-1}}\\
&=&-\log_32\\
&=&\log_3\frac{1}{2}
\end{eqnarray}\)
とすることもできます。
実際の試験中はこんなていねいな計算はしなくて良いですよ。
計算ミスしない程度に済ませて、ちゃっちゃと次に進みましょう。
⇒ センター試験数学2B2019年度第2問(微分と積分)の解説
第\(2\)問は微分と積分の基礎です。
極値、接線、面積と全般ですが文字処理の仕方でかかる時間の差が出ます。
第\(\,1\,\)問の三角関数、指数対数というセットは\(2020\)年度も同じです。
