センター試験２０１８年、平成３０年度の数学ⅡＢの第４問の解答解説です。
選択問題になるベクトルですが統計的推測を選択しないことが多いので実質必修で最後の問題となります。
今回の問題は、平面ベクトルで、誘導もていねいにされているので基本的な作業をしていれば高得点できたのではないでしょうか。
問題は大学入試センターにもあります。
第４問（選択問題）ベクトル
ベクトルに限りませんが図形の情報が問題にあるときは必ず図を書きましょう。
問題をみる前に確認しておきます。
ベクトルでは、
・始点をひとつにそろえる
・平面なら基底の２つのベクトルで、すべてのベクトルを表す
先ずこの二つはいつも考えておきましょう。
ベクトルをどうこうする前に図を書いて位置関係を把握しておきましょう。
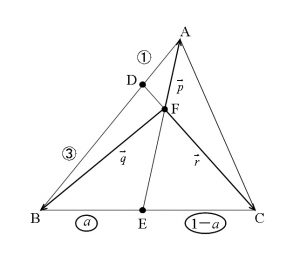
ここでは問題でもベクトルがいくつか与えられているし、始点はFとしたほうがいいですね。
\( \overrightarrow {FA}=\overrightarrow {p}\)
\( \overrightarrow {FB}=\overrightarrow {q}\)
\( \overrightarrow {FC}=\overrightarrow {r}\)
とされています。
（１）（２）の目的はどちらも同じです。
「 \( \color{red}{\overrightarrow {p}} , \color{red}{\overrightarrow {q}}\) を用いて表す」
これはベクトルの基本通りですね。
ベクトルの大きさ
（１）
始点をFに換えることで
\( \overrightarrow {AB}=\overrightarrow {FB}-\overrightarrow {FA}\\ \\
=\underline{\overrightarrow {q}-\overrightarrow {p}}\)
次に、ベクトルの大きさをみたらとにかく２乗します。
\( |\overrightarrow {AB}|^2=|\overrightarrow {q}-\overrightarrow {p}|^2\\ \\
=|\overrightarrow {q}|^2-2\overrightarrow {q}\cdot \overrightarrow {p}+|\overrightarrow {p}|^2\)
よって
\( |\overrightarrow {AB}|^2=|\overrightarrow {p}|^2-\fbox{2}\overrightarrow {p}\cdot \overrightarrow {q}+|\overrightarrow {q}|^2\) ･･･①
ア：② イ：２
ここまでは機械的に処理できますね。
内分点のベクトル
（２）
点 D は辺 A Bを \( 1:3\) に内分する点なので
\( \overrightarrow {FD}=\displaystyle \frac{3\cdot \overrightarrow {p}+1\cdot \overrightarrow {q}}{1+3}\\ \\
=\displaystyle \frac{3 \overrightarrow {p}+\overrightarrow {q}}{4}\)
よって
\(\displaystyle \overrightarrow {FD}=\frac{\fbox{3}}{\fbox{4}}\overrightarrow {p}+\frac{\fbox{1}}{\fbox{4}}\overrightarrow {q}\) ･･･②
ウ：３ エ：４ オ：１ カ：４
ここもできて当たり前といって良いほど考えることがありません。
ベクトルの線型性
（３）
ここは目的を書いてくれています。
点 D は直線 FC 上にあるから実数 \( s\) を用いて
\( \overrightarrow {FD}=s\overrightarrow {r}\)
と表すことができるので、②を左辺として利用し、
\( \displaystyle \frac{3}{4}\overrightarrow {p}+\displaystyle \frac{1}{4}\overrightarrow {q}=s\overrightarrow {r}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 3\overrightarrow {p}+\overrightarrow {q}=4s\overrightarrow {r}\)
移項すれば
\( \overrightarrow {q}=\fbox{-3}\overrightarrow {p}+\fbox{4}s\overrightarrow {r}\) ･･･③
キク：－３ ケ：４
「点 E が直線 FA 上にあるから」、という意味で、
実数 \( t\) を用いて表すと \( \overrightarrow {FE}=t\overrightarrow {p}\) となります。
点 E は辺 BC を \(a:(1-a)\) に内分する点なので
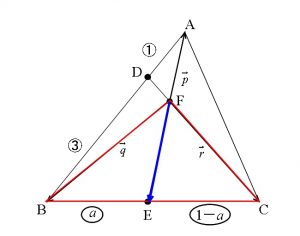
\( \overrightarrow {FE}=(1-a)\overrightarrow {FB}+a\overrightarrow {FC}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} t\overrightarrow {p}=(1-a)\overrightarrow {q}+a\overrightarrow {r}\)
移項して
\( -(1-a)\overrightarrow {q}=-t\overrightarrow {p}+a\overrightarrow {r}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (1-a)\overrightarrow {q}=t\overrightarrow {p}-a\overrightarrow {r}\)
\( 0< a< 1\) なので \( 1-a\neq 0\) だから両辺を \( 1-a\) で割って \(\displaystyle \overrightarrow {q}=\frac{t}{\fbox{1}-\fbox{a}}\overrightarrow {p}-\frac{\fbox{a}}{1-a}\overrightarrow {r}\) ･･･④
コ：１ サ：a シ：a
③と④は同じベクトルを表していて、\( \overrightarrow {p}\,,\,\overrightarrow {r}\) の係数は一致するので
\( \begin{cases}
\hspace{10pt}-3=\displaystyle \frac{t}{1-a} \\ \\
\hspace{15pt}4s=-\displaystyle \frac{a}{1-a}
\end{cases}
\hspace{5pt} \Leftrightarrow \hspace{5pt}
\begin{cases}
\hspace{10pt}-3(1-a)=t \\ \\
\hspace{15pt}s=\displaystyle \frac{-a}{4(1-a)}
\end{cases}\)
解答欄の順に並べると、
\( s=\displaystyle \frac{\fbox{-a}}{\fbox{4}(1-a)}\)
\( t=\fbox{-3}(1-a)\)
スセ：－a ソ：４ タチ：－３
内積と大きさ
（４）
ここも目的を書いてくれていますのでやることやれば誘導なしでも出せますが、何も考えなくても答が出てくるので誘導にのる方が楽です。
本当なら図を書いて位置関係を確認しますが、簡単な図を書き直すだけで、関係式を出しているうちに答がでています。
\( |\overrightarrow {AB}|=|\overrightarrow {BE}|\)
ベクトルの大きさの関係です。
ベクトルの大きさをみたらとにかく２乗するのですが、誘導にあります。
\( |\overrightarrow {AB}|^2=|\overrightarrow {BE}|^2\)
この左辺と右辺を別々に表し「等しい」とおけば内積が求まる。
というのが誘導の内容です。
「①により」と親切に書いてくれています。
これをみていないと、
\( |\overrightarrow {AB}|^2\\ \\
=|\overrightarrow {FB}-\overrightarrow {FA}|^2\\ \\
=|\overrightarrow {q}-\overrightarrow {p}|^2\\ \\
=|\overrightarrow {q}|^2-2\overrightarrow {q}\cdot \overrightarrow {p}+|\overrightarrow {p}|^2\)
を再度計算することになります。
\( |\overrightarrow {p}|=1\) のときを考えているので、
\( |\overrightarrow {AB}|^2=1-2\overrightarrow {p}\cdot \overrightarrow {q}+|\overrightarrow {q}|^2\) ･･･⑤
また始点を F にすることで
\( |\overrightarrow {BE}|^2=|\overrightarrow {FE}-\overrightarrow {FB}|^2\)
\( \overrightarrow {FE}=t\overrightarrow {p}\) だったので
\( t=-3(1-a)\) と \( |\overrightarrow{p}|^2=1\) から
\( |\overrightarrow {BE}|^2=|t\overrightarrow {p}-\overrightarrow {q}|^2\\ \\
=|-3(1-a)\overrightarrow {p}-\overrightarrow {q}|^2\\ \\
=\{-3(1-a)\}^2|\overrightarrow {p}|^2+6(1-a)\overrightarrow {p}\cdot \overrightarrow {q}+|\overrightarrow {q}|^2\\ \\
=9(1-a)^2|\overrightarrow {p}|^2+6(1-a)\overrightarrow {p}\cdot \overrightarrow {q}+|\overrightarrow {q}|^2\\ \\
=9(1-a)^2+6(1-a)\overrightarrow {p}\cdot \overrightarrow {q}+|\overrightarrow {q}|^2 ･･･⑥\)
⑤と⑥が等しいことから \( |\overrightarrow {q}|^2\) が消えて
\( 1-2\overrightarrow {p}\cdot \overrightarrow {q}=9(1-a)^2+6(1-a)\overrightarrow {p}\cdot \overrightarrow {q}\)
見やすくするために \( \overrightarrow {p}\cdot \overrightarrow {q}=A\) とおきます。
\( 1-2A=9(1-a)^2+6(1-a)A\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} -2A-6(1-a)A=9(1-a)^2-1\\ \\
\hspace{5pt} \Leftrightarrow \hspace{15pt} (6a-8)A=9(1-2a+a^2)-1\\ \\
\hspace{5pt} \Leftrightarrow \hspace{10pt} 2(3a-4)A=9-18a+9a^2-1\\ \\
\hspace{5pt} \Leftrightarrow \hspace{10pt} 2(3a-4)A=9a^2-18a+8\\ \\
\hspace{5pt} \Leftrightarrow \hspace{10pt} 2(3a-4)A=(3a-4)(3a-2)\\ \\
\hspace{5pt} \Leftrightarrow \hspace{20pt} 2A=(3a-2)\\ \\
\hspace{5pt} \Leftrightarrow \hspace{25pt} A=\displaystyle \frac{3a-2}{2}\)
つまり
\( \overrightarrow {p}\cdot \overrightarrow {q}=\displaystyle \frac{\fbox{3a}-\fbox{2}}{\fbox{2}}\)
トナ：３a ニ：２ ヌ：２
最後は少し計算力を試されていますが、全体的にベクトルの基本問題でした。
何度も言っていますが、
センター試験が無くなって、共通テストになっても数学の基本が変わるわけではありませんよ。