ある点を通りもう一つの直線に垂直、または平行という条件の直線の方程式を求めるといった問題で、いきなり式で処理している人は数学を苦手なままにしているかもしれません。
公式があるので使うのは良いのですが、応用出来るようにするための求め方をお伝えしておきます。
誘導される問題では使えませんし、ここでは簡単にしか説明しませんが位置関係を表すにはベクトルも便利ですよ。
垂直な位置関係の確認
\( A(1\,,\,2)\,,\,B(4\,,\,1)\) とする。
線分 \( AB\) を \( 1:2\) に内分する点を通り \( AB\) に垂直な直線の方程式を求めよ。
2直線の傾きが \( m\,,\,n\) のとき垂直条件 \( mn=-1\) というのがありますが、こんなものは後回しでいいです。
先ずやらなければならないのは、
「位置関係をつかむ図を書くこと」
です。
この場合は座標上での図示になりますが、簡単なもので良いので書きましょう。
数学が得意な人が図を書かずに解いているかもしれませんが、どうでもいいです。
図を書くことで解法の選択肢を増やすことが可能になるので、数学苦手だと感じている人には先ずやっておいて欲しいポイントです。
問題に入りましょう。
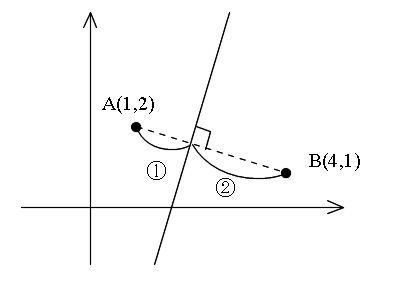
求めるものは『直線の方程式』だからといって「方程式」の問題と思わないで下さいね。
方程式には違いないけど一次関数の問題です。
問題にある点や位置関係がどうなるか書いて見て、条件を書き出して見るといろいろと見えてきます。
内分点の座標
先ず内分点の座標は必要です。
\( (a\,,\,b),(c\,,\,d)\) を \( m:n\) に内分する点 \( (p\,,\,q)\) は、
\(\displaystyle \color{red}{(\,p\,,\,q\,)}=\left(\color{red}{\frac{na+mc}{m+n}\,,\,\frac{nb+md}{m+n}}\right)\)
です。
\( (a\,,\,b),(c\,,\,d)\) を \( m:n\) に外分する点 \( (p\,,\,q)\) は、
\(\displaystyle \color{red}{(\,p\,,\,q\,)}=\left(\color{red}{\frac{na-mc}{m-n}\,,\,\frac{nb-md}{m-n}}\right)\)
です。
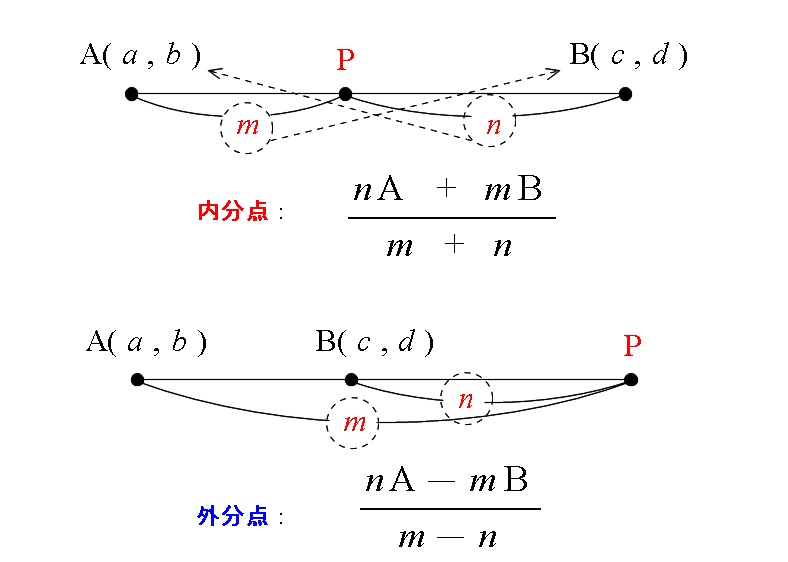
(外分は \( m:(-n)\) に内分と考えると同じです。)
これらは良いですよね?
\( A(1\,,\,2)\hspace{5pt}B(4\,,\,1)\) を \( 1:2\) に内分する点Pとすると、
点Pの座標は
\( \left(\displaystyle \frac{2\times 1+1\times 4}{1+2}\,,\,\displaystyle \frac{2\times 2+1\times 1}{1+2}\right)=\left(2\,,\,\displaystyle \frac{5}{2}\right)\)
もう一つ必要な条件は、「ABに垂直」です。
これはいろいろな方法があります。
ベクトルを使うと早いですが、ここでは直線の垂直条件を使いましょう。
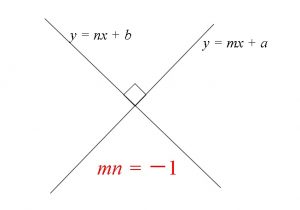
直線の垂直条件
2本の直線が‘軸’に垂直(平行)ではないとき、
『直交する2本の直線の「傾きの積」は-1になる。』
つまり、
\( y=\color{red}{m}x+a\) と \( y=\color{red}{n}x+b\) が垂直のとき
\( \large{\color{red}{mn=-1}}\)
直線ABの傾きは、
\( \displaystyle \frac{1-2}{4-1}=\displaystyle \frac{-1}{3}\)
だから求める直線を \( \ell\) とするときの \( \ell\) の傾き \( m\) は
\( \displaystyle \frac{-1}{3}\times m=-1 \hspace{5pt} \Leftrightarrow \hspace{5pt} m=3\)
です。
そして点 \(\displaystyle P\left(2\,,\,\frac{5}{3}\right)\) を通ることより求める方程式は、
\( y-\displaystyle \frac{5}{3}=3(x-2) \hspace{5pt} \Leftrightarrow \hspace{5pt} \underline{y=3x-\displaystyle \frac{13}{3}}\)
※
傾き \( \color{blue}{m}\) で点 \( (\color{red}{a}\,,\,\color{red}{b})\) を通る直線は
\( y-\color{red}{b}=\color{blue}{m}(x-\color{red}{a})\)
なので覚えておくといいです。微分の接線でも必ず必要になりますよ。
使った条件(与えられた条件でもある)は、「AB⊥ℓ」および「点Pを通る」だけです。
ベクトルを使うともっと簡単(おなじ?)になるのでやっておきましょう。
ベクトルの利用
求める直線 \( \ell\) 上の点を \( Q(x,y)\) とすると、
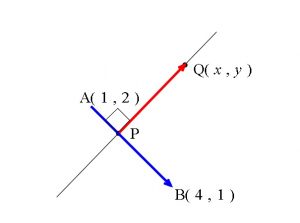
\( \overrightarrow {PQ}\cdot \overrightarrow {AB}=0\)
つまり「内積が0」が条件です。
\( \overrightarrow {PQ}
=\overrightarrow {OQ}-\overrightarrow {OP}
=\left(x-2\,,\,y-\displaystyle \frac{5}{3}\right)\)
\( \overrightarrow {AB}
=\overrightarrow {OB}-\overrightarrow {OA}
=(3\,,\,-1)\)
よって、
\( 3(x-2)-1\left(y-\displaystyle \frac{5}{3}\right)=0\)
としても同じ答えは得ることが出来ます。
総合演習する際はどちらでも使えるようになっておくと良いですね。
分野ごとの基本ももちろん大切ですが、すべての分野に共通する基本作業の方が大切ですよ。