長方形の紙の角を切り取ってきる直方体の体積(容積)の最大値を微分を使って求める問題の解説です。
微分を利用すると関数の増減が分かりますので、増減表だけで片付くのですが定義域には注意しておきましょう。
それと、重要なポイントがありますので確認しておきます。
直方体の容積を求める関数で表す
「長方形」や「直方体」などの言葉は図形を表しています。
だからグラフや増減表を考える前にイメージできる「図」を書きましょう。
図を書くのと書かないのとでは問題の難易度が全く違うように感じますよ。
縦30cm,横14cmの長方形の紙の四隅からそれぞれ1辺 \( x\) cmの正方形を切り取り残りで箱を作る。
この箱の容積が最大になるときの \( x\) の値と容積の最大値を求めよ。
文章題って難しいって、中学の頃から思っている人いるでしょう?
理由は簡単で、日本語だけで考えるから難しく見るんですよね。
日本語を数学の言葉に換えましょう。
図を書くのです。図は立派な数学の言葉ですよ。
「縦30cm,横14cmの長方形の紙の四隅からそれぞれ1辺 \( x\) cmの正方形を切り取り残りで箱を作る。」
これを図にしてみましょう。
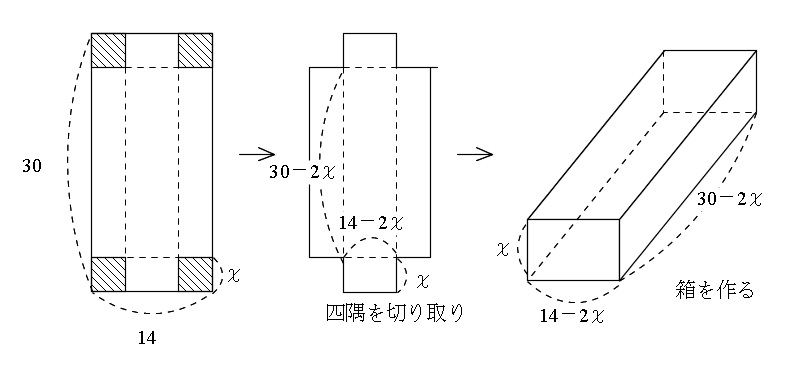
この箱の体積を最大にする \( x\) と最大値を求めれば良いのです。
箱の体積を \( V(x)\) とすると、
\( V(x)=(30-2x)(14-2x)x\)
と関数自体はすぐに求まりますが忘れているものがあります。
定義域、つまり、\( x\) の範囲です。
\( x\) は切り取る長さで、
一辺から2つ切り取るから \( 2x\) の範囲は
\( 0\,< \,2x\,< \,14\hspace{5pt} \Leftrightarrow \hspace{5pt} 0\,< \,x\,< \,7\) \( x=0\,,\,7\) のときは箱にならないので等号は省いていいでしょう。 つまり \( 0\,<\,x\,<\,7\) における
\( V(x)=(30-2x)(14-2x)x\\ \\ =4x^3-88x^2+420x\)
の最大値を求めれば良いことになります。
定義域に範囲がなければ \( V(x)\) はいくらでも大きくなり最大値はないことは気がつきますね。
最大値や最小値は増減表で求まる
3次「関数」の最大・最小問題ではグラフを活用しますが必需品となるのが『増減表』です。
『微分』に限らず2次関数でも増減表は使えますよ。
2次関数は使わなくても平方完成、グラフから見て取れるだけで、増減表を使っても良いのです。
「関数」の最大最小は増減表さえ書ければ何とかなる、といっても良いくらいです。
では解答に入りましょう。
箱の体積を \( V(x)\) とすると、縦、横、高さは正であるから、
\( 30-2x>0 かつ 14-2x>0 かつ x>0 \\ \\
\Leftrightarrow 0\,< \,x\,< \,7\)
において
\( V(x)=(30-2x)(14-2x)x\\ \\ =4x^3-88x^2+420x\)
微分して
\( V'(x)=12x^2-176x+420\\ \\ = 4(3x-35)(x-3)=0\)
から \(\displaystyle x=3\,,\,\frac{35}{3}\) に注意して定義域の範囲の増減表を書くと
| \( x\) | \( (0)\) | \( \cdots \) | \( 3\) | \( \cdots \) | \( (7)\) |
| \( V'(x)\) | \( +\) | \( 0\) | \( -\) | ||
| \( V(x)\) | \( \nearrow\) | \( 576\) | \( \searrow\) |
よって、\(x=3\) のとき極大かつ最大で
最大値 \( \underline{576}\)
『増減表を書かないというのは微積の問題では考えられない』
というくらい重要ですよ。
この問題ではグラフは必要ありませんがグラフも重要です。
最大値最小値の存在確認
ところで、この問題では定義域の両端は含まれていません。
このような場合、増加減少によっては最大値が無い場合もありますが、
極大値が存在していて、その値が最大になっているので最大値として良いのです。
例えば
\( y=x^2 (-1\,\color{red}{<} \,x\,\color{red}{<} \,2)\)
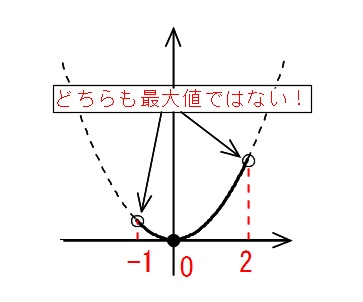
には最小値は存在しますが、最大値は存在しませんよ。
次も同じような問題ですが手順だけ説明しておきますのでやって見てください。
横45cm、縦24cmの長方形の紙の4隅から、同じ大きさの正方形を切り取ってふたの無い箱をつくるとき、この箱の容積を最大にするには、切り取る正方形の1辺の長さをいくらにすれば良いか。
図形の最大最小問題なので、先ずは図を書いておきましょう。
(ここは自分で書かないと意味がありません。)
次に定義域です。
切り取る正方形の1辺の長さを \( x\) として
\( 45-2x>0\,,\,24-2x>0\,,\,x>0\)
をすべて満たす範囲が定義域になります。
この範囲で増減表を書いて最大となる \( x\) を見つけます。
略解です。
箱の容積を \( V(x)\) とすると
\( V(x)=(45-2x)(24-2x)x\\ \\
=4x^3-138x^2+1080x\)
微分すると
\( V'(x)=12x^2-276x+1080\\ \\
=12(x^2-23x+90)\\ \\
=12(x-5)(x-18)\)
なので
\( V'(x)=0 \hspace{5pt} \Leftrightarrow \hspace{5pt} x=5\,,\,18\)
となる。
\( 45-2x>0\,,\,24-2x>0\,,\,x>0 \\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 0\,< \,x\,< 12\) の範囲で増減表を書くと、
| \( x\) | \( 0 \) | \( \cdots \) | \( 5 \) | \( \cdots \) | \( 12 \) |
| \( V'(x)\) | \( +\) | \( 0\) | \( – \) | ||
| \( V(x)\) | \( \nearrow \) | \( \mathrm{Max} \) | \( \searrow \) |
よって1辺の長さを5cmにすれば良い。
微分さえできれば増減表を書いて終わりです。