三角関数の最大値や最小値を求める問題を解くのに微分が使える問題の解説です。
数学Ⅲの三角関数の微分ではありません。数学Ⅱの範囲でできることです。
三角関数の2次式や3次式でも同じように増減表が使えるという微分のちょっとした応用ですが、
サインやコサインの置換を行うので定義域に気をつけておかなければなりません。
三角関数を微分する前に置換する
三角関数の微分というと
\( (\sin x)’=\cos x\)
\( (\cos x)’=-\sin x\)
などの数学\(\,\mathrm{Ⅲ}\,\)の内容を思い出しますがここでは違います。
サインやコサインで表されている関数を置換することで整関数に書き換え、
その関数に微分を使って最大値最小値を求めようという問題です。
置換(置きかえ)するので定義域の変化に注意していれば普通に増減表が書けます。
三角関数の復習にもなるので例題で説明します。
次の問いに答えよ。
(1)加法定理を用いて等式
\( \cos 3\theta=4\cos^3\theta-3\cos\theta\)
が成り立つことを示せ。
(2)関数 \( f(\theta)=\cos 3\theta -\cos^2\theta +\cos \theta\)
の最大値と最小値を求めよ。
ただし、\(\displaystyle 0\,≦\, \theta \,≦\,\frac{2}{3}\pi\) とする。
『加法定理を用いて』と指示していますので、「覚えているから、、、」ではダメです。
加法定理の確認
再度の確認になりますが、
『加法定理』
\( \color{red}{\sin (\alpha+\beta)=\sin\alpha \cos\beta+\cos \alpha \sin \beta}\)
\( \color{blue}{\cos (\alpha+\beta)=\cos\alpha \cos\beta-\sin \alpha \sin \beta}\)
です。
覚えておくのはこの2つで十分足ります。
3倍角の公式の証明
「加法定理を用いて」
\(\hspace{10pt} \cos 3\theta=4\cos^3\theta-3\cos\theta\)
を示しましょう。
\( \color{red}{\cos\theta}\) のみで表すことを目標にします。
\(\hspace{10pt} \cos \underline{3\theta}\\
=\cos (\underline{2\theta+\theta}) \\
=\cos \underline{\underline{2\theta}}\cos\theta-\sin \underline{\underline{2\theta}}\sin\theta\\
=\cos (\underline{\underline{\theta+\theta}})\cos \theta – \sin(\underline{\underline{\theta + \theta}})\sin\theta\\
=(\cos\theta \cos\theta- \sin\theta \sin\theta )\cos\theta-(\sin\theta \cos\theta + \cos\theta \sin\theta)\sin\theta\\
=(\cos^2\theta-\sin^2\theta)\cos\theta-(2\sin\theta \cos\theta )\sin\theta\\
=\{\cos^2\theta-(1-\cos^2\theta)\}\cos\theta – 2\sin^2\theta \cos\theta\\
=(2\cos^2\theta-1)\cos\theta -2(1-\cos^2\theta) \cos\theta\\
=2\cos^3\theta-\cos\theta-2(1-\cos^2\theta)\cos\theta\\
=2\cos^3\theta-\cos\theta-2\cos\theta+2\cos^3\theta\\
=4\cos^3\theta-3\cos\theta\)
すべてに「加法定理」そのものを使って示しましたが、
最初の段階で加法定理を利用した時点で、
倍角の公式を使って簡略しても良いと思いますよ。
それと、途中を飛ばすと分かりにくいと思うのでものすごく細かく書き出しました。
加法定理の利用がはっきりと書かれていれば途中の計算は書かなくても大丈夫ですが、
自分でも導けるように、一度は計算しておいてくださいね。
これで、\(\hspace{4pt} \cos3\theta\hspace{4pt}\)の公式が導けたとして、
(2)「 関数
\( f(\theta)=\cos 3\theta -\cos^2\theta +\cos \theta\\ \\
\left(\,0\,≦ \,\theta \, ≦ \,\displaystyle \frac{2}{3}\pi \right)\)
の最大値と最小値」
です。
関数は\(\hspace{4pt}\cos\hspace{4pt}\)で統一されていますがこのままでは増減は分かりません。
増減表を書くときの注意点
「置換」→「定義域の変換」をします、が(1)の誘導をお忘れなく。
(2)
(1)より
\(\begin{eqnarray} f(\theta)&=&\underline{\cos 3\theta} -\cos^2\theta +\cos \theta\\
&=&\underline{4\cos^3\theta -3\cos\theta}-\cos^2\theta+\cos\theta\\
&=&4\cos^3\theta -\cos^2\theta-2\cos\theta
\end{eqnarray}\)
ここで\(\hspace{4pt}cos \theta=t\hspace{4pt}\)と置換したら、
いったん三角関数から離れ\(\,t\,\)の関数と見ます。
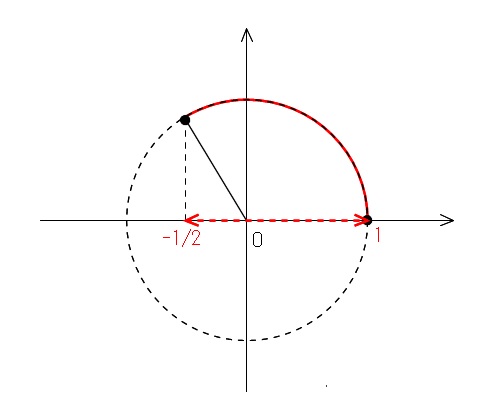
\(\hspace{4pt}\cos\theta=t\hspace{4pt}\)とおくと、
\(\hspace{10pt}\displaystyle 0\,≦\,\theta \, ≦\,\frac{2}{3}\pi\)
から
\(\hspace{10pt}\displaystyle -\frac{1}{2}\,≦ \,t \, ≦ \,1 ・・・①\)
と定義域が変わります。
\(\hspace{10pt} f(\,\color{red}{\theta}\,)=g(\,\color{blue}{t}\,)\)
と置き換えて、
(\(\hspace{4pt}\color{red}{\theta}\hspace{4pt}\)の関数から\(\hspace{4pt}\color{blue}{t}\hspace{4pt}\)の関数へと見方を変えます。)
\(\hspace{10pt} g(t)=4t^3-t^2-2t \\
\hspace{7pt} \left(-\displaystyle \frac{1}{2}\,≦ t\,≦\,1\right)\)
の最大・最小を求めれば良いので3次関数の最大最小問題に変わりました。
「最大・最小」⇒ 「増減表」です。
\(\begin{eqnarray} g'(t)&=&12t^2-2t-2\\
&=&2(6t^2-t-1)\\
&=&2(2t-1)(3t+3)=0
\end{eqnarray}\)
から
\(\hspace{10pt} t=\displaystyle \frac{1}{2}\,,\,-\displaystyle \frac{1}{3}\)
①の範囲で増減表を書きます。
| \( t\) | \( -\displaystyle \frac{1}{2}\) | \( \cdots \) | \( -\displaystyle \frac{1}{3}\) | \( \cdots \) | \( \displaystyle \frac{1}{2}\) | \( \cdots \) | \( 1\) |
| \( g'(t)\) | \( +\) | \( 0\) | \( -\) | \( 0\) | \( +\) | ||
| \( g(t)\) | \( \mathrm{A}\) | \( \nearrow\) | \( \mathrm{B}\) | \( \searrow\) | \( \mathrm{C}\) | \( \nearrow\) | \( \mathrm{D}\) |
となります。
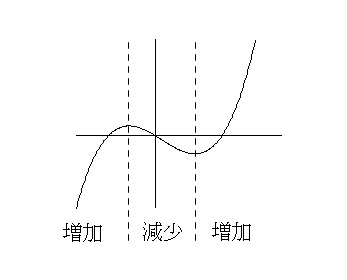
この増減表の\(\hspace{4pt}g'(t)\hspace{4pt}\)の増加区間と減少区間ですが、
「3次関数のグラフがコブ2つ」
ということを頭に置いておくと早いですよ。
ただし、極値となる\(\,t\,\)が増減表の区間に入っていない場合などは注意して下さい。
確実なのは、その区間で具体的な数値を代入することです。
例えば、
\( g'(t)=12t^2-2t-2\)
なので
\(\begin{eqnarray} g'(-1)&=&12(-1)^2-2(-1)-2=12\,(\,>\,0)\\
g'(0)&=&-2\,(\,<\,0)\\
g'(1)&=&12(1)^2-2(1)-2=8\,(\,>\,0)\end{eqnarray}\)
のようにある部分の増減が「+」「-」で一致しているか確認するのです。
\(\hspace{4pt} g'(t)=0\hspace{4pt}\)から区切ったそれぞれの区間では、
\(\hspace{10pt} g(t)\)の増減は変化しないので、
1つ調べれば「+」か「-」が分かるので増減表に書き込んでいけばはっきりしますよ。
さて、増減は分かりましたが最大・最小ははっきりしません。
増減表に書き込んである
\( \mathrm{A\,,\,C}\hspace{4pt}\)はどちらが小さいのか、
\( \mathrm{B\,,\,D}\hspace{4pt}\)はどちらが大きいのか、
最大・最小ははっきりしていません。
手間のかかる計算ですがきっちり求めておきましょう。(自分で)
\(\begin{eqnarray}\displaystyle
\mathrm{A}&=&g\left(-\displaystyle \frac{1}{2}\right)=\displaystyle \frac{1}{4}\\
\mathrm{B}&=&g\left(-\displaystyle \frac{1}{3}\right)=\displaystyle \frac{11}{27}\\
\mathrm{C}&=&g\left(\displaystyle \frac{1}{2}\right)=-\displaystyle \frac{3}{4}\\
\mathrm{D}&=&g(1)=1\end{eqnarray}\)
グラフの増減から最小となるとすれば
\(\hspace{10pt}\mathrm{A}\hspace{4pt}\)か\(\hspace{4pt}\mathrm{C}\)
のどちらかで
\(\hspace{4pt}\mathrm{A\,>\,C}\)
なので最小値は\(\hspace{4pt}\mathrm{C}\hspace{4pt}\)で
\(\displaystyle t=\frac{1}{2}\hspace{4pt}\)のとき\(\hspace{4pt}\displaystyle -\frac{3}{4}\)
最大となるとすれば\(\hspace{4pt}\mathrm{B}\hspace{4pt}\)か\(\hspace{4pt}\mathrm{D}\)
のどちらかで
\(\hspace{4pt}\mathrm{B\,<\,D}\)
なので最大値は\(\hspace{4pt}\mathrm{D}\hspace{4pt}\)で
\(\hspace{10pt} t=1\hspace{4pt}\)のとき\(\hspace{4pt}1\)
ただし、置換した\(\hspace{4pt}\color{blue}{t}\hspace{4pt}\)を\(\hspace{4pt}\color{red}{\theta}\hspace{4pt}\)に戻した値を出して答えとします。
\(\hspace{10pt}\displaystyle \color{blue}{t}=\cos\color{red}{\theta}=\frac{1}{2}\)
つまり
\(\displaystyle \color{red}{\theta}=\frac{\pi}{3}\hspace{4pt}\)のとき最小値\(\displaystyle \underline{ -\frac{3}{4} }\)
\(\hspace{10pt} \color{blue}{t}=\cos\color{red}{\theta}=1\)
つまり
\( \color{red}{\theta}=0\hspace{4pt}\)のとき最大値\( \underline{ 1 }\)
置換してしまえば三角関数の問題ではなく、分かりやすい整関数なりますので、
置換して簡単な関数に変換するということと、
やはり『増減表』は重要ですね。
⇒ 3次方程式の解の個数を求める問題を関数として微分で解く方法
方程式でも増減表やグラフが大きな役割をしていることを確認しましょう。
増減表は関数の最大最小を視覚で見つけることができます。
整関数の微分積分はそれほど時間がかからず使える様になりますよ。