数学的帰納法の不等式の証明問題への利用方法です。
帰納法は等式、不等式どちらにも使えますが、不等式では大小関係をはっきりさせるためにちょっとした工夫が必要になってきます。
等式の証明ができるようになってからで良いですが、大小関係を示す比較のしかたをいくつか覚えておきましょう。
数学的帰納法については説明してありますので確認しておいてください。
不等式の証明例題を見ながら説明して行きます。
不等式の証明では『評価』の説明をした方が良いのですが、数学\(\,\mathrm{Ⅲ}\,\)に譲るということでカットします。笑
なくても理解できる範囲で説明をしておきますので参考にして下さい。
数学的帰納法を利用する不等式の証明
\(\,n\,\)が\(\,5\,\)以上の自然数であるとき、
不等式 \( 2^n\,>\, n^2\) が成り立つことを証明せよ。
不等式の証明は
\( a\,> \,b\hspace{5pt} \Leftrightarrow \hspace{5pt}a-b\,> \,0\)
が言えれば良いのですが、
\(\hspace{10pt} 2^n-n^2 \,> \,0\)
をいうのは簡単ではありません。
\( n=3\) のとき \( 2^3-3^2=8-9=-1\,< \,0\)
\(n=4\) のとき \( 2^4-4^2=16-16=0\)
\(n=5\) のとき \( 2^5-5^2=32-25=7\,> \,0\)
\( n=6\) のとき \(2^6-6^2=64-36=28\,> \,0\)
と確かに\(\,n\,≧\,5\,\)において成り立っていそうですが、
推測でしかなく、確実(論理的)ではありません。
数学的帰納法を使いますが、不等式は目的となる右辺の式が見つけにくいです。
\(\hspace{10pt} k\hspace{7pt} \rightarrow \hspace{7pt} k+1\)
を代入することは簡単ですが、それを示すことが難しい場合が多いのです。
不等式を二段階の大小比較で証明する
ここでは\(\,2^k\,>\,k^2\)を仮定したとして
\(\hspace{10pt}2^{k+1}\,>\,(\,k+1\,)^2\)
を示すことになります。
(すぐに気がつく人は十分慣れているといって良いでしょう。)
だから、示したい不等式の間にもう一つの不等式を連立するというちょっとした工夫をします。
どういうことかと言うと、
\( A\,> \,B\) を示すのに、
\( A\,> \,\color{red}{C} , \color{red}{C}\,> \,B\)
となる間の大きさ\(\,\color{red}{C}\,\)を探すのです。
この間に入る\(\,C\,\)が見つかれば、
\(\hspace{10pt}A\,>\,\color{red}{C}\,>\,B\)
となり、\(A\,>\,B\)も示せますからね。
ただ、\( \,\color{red}{C}\,\)を見つけるのが簡単にはいかない場合があります。
そのため闇雲に探すのではなく、
\( A\,> \,C \,> \,B\)
となる\( \,B\,\)の関係式に似た関係式で
「\(\,B\,\)より少し大きいもの」
を仮定してから探すとうまくいくことが多いです。
単純に\(\,C-B\,>\,0\,\)を示すのも手です。
今回の様に直接は示せないので
「\( \,A\,\)よりは小さいもの\(\,C\,\)」
を探して「差をとる」ということですね。
不等式の証明はいろいろなパターンがあるので、一概には言えません。
ある程度の演習例題(パターンがあります)には目を通しておくといいでしょう。
では、
「\(\,n\,\)は\(\,5\,\)以上の自然数,\( 2^n \,> \,n^2\) 」
を数学的帰納法を用いて証明してみましょう。
不等式の証明の数学的帰納法の流れ
数学的帰納法の流れとしては
ⅰ)\(\,n=5\,\)のとき\( \,5^2=32\,> \,5^2\,\)より成り立つ。
ⅱ)\(\,n=k\,\)のとき\(\, 2^k\,>\,k^2\,\) ・・・①
が成り立つと仮定し、
\(\,n=k+1\,\)のとき\(\, 2^{k+1}\,> \,(k+1)^2\) ・・・②
が示せれば良いのです。
左辺を見ます。
\( k\,\rightarrow \,k+1\) ということは
\(\hspace{10pt} 2^{k+1}=2\cdot 2^k\)
で\(\,2\,\)が\(\,k\,\)のときよりもう一回多くかけられるということで、
①の仮定から
\(\hspace{10pt} \color{red}{2^k}\,>\,\color{blue}{k^2}\)
なので
\(\hspace{10pt} 2^{k+1} =\underline{2\cdot \color{red}{2^k}}\,> \,\underline{2\cdot \color{blue}{k^2}}\)
は仮定が正しければ成り立ちます。
ここで仮定を利用するのは等式の証明の場合と同じです。
次にやることは見えてきました。
\(\hspace{10pt} \underline{2\cdot k^2\,> \,(k+1)^2}\) ・・・③
を示せば、
\(\hspace{10pt} \color{red}{2^{k+1}}\,> \underline{\,2\cdot k^2\,> \,\color{blue}{(k+1)^2}}\)
なので
\(\hspace{10pt} \color{red}{2^{k+1}}\,> \,\color{blue}{(k+1)^2}\)
が示せます。
ここで、大小比較ですが整式どうしなので左辺から右辺を引いてみましょう。
③の左辺から右辺を引いて
\(\hspace{10pt} 2\cdot k^2-(k+1)^2\\
=2k^2-(k^2+2k+1)\\
=2k^2-k^2-2k-1\\
=k^2-2k-1\\
=(k-1)^2-2\)
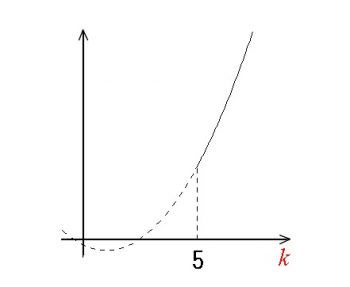
これは
\(\,k\,≧\,5\,\)において\(\,(k-1)^2-2\,>\,0\)
であるから(軸の位置から明らかでしょう。)
\(\hspace{10pt} 2\cdot k^2-(k+1)^2\,> \,0\\
\Leftrightarrow \hspace{5pt} 2\cdot k^2 \,> \,(k+1)^2\)
よって、
\(\hspace{10pt}2^{k+1}\,> 2\cdot k^2 \,> \,(k+1)^2\)
が言えました。
つまり、\( n\,≧ \,5\) において、
① \(2^k\,> \,k^2\)を仮定すると
② \( 2^{k+1}\,> \,(k+1)^2\)が成り立つ。
ⅰ)ⅱ)より
\(\,n\,\)が\(\,5\,\)以上の自然数のとき不等式\(\,2^n\,>\,n^2\,\)が成り立つ。
(終わり)
グラフで見ると
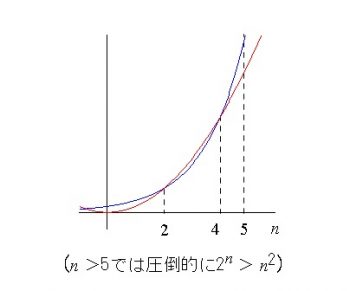
\( n\,>\,5\,\)では圧倒的に\(\,2^n\,>\,n^2\)
です。
等式の証明のときも同じことが言えますが、
\( n=1\,\)で成り立つことが言えれば\(\,n\,≧\,1\,\)で成り立つことが言えるように、
\( n=5\,\)で成り立つことを言っているので\(\,n\,≧\,5\,\)では帰納的に成り立つことが言えているのですよ。
数学的帰納法は推測した数列の一般項の証明にも使えます。
数学的帰納法までで数列の項目にはおおよそ目を通したことになります。
もう一度全体を見直しておきましょう。