三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない？

三角比の問題で三角形の角度が２つ分かっている（与えられている）のに正弦定理か余弦定理を使うと考えても、どちらも使えそうにないときがあります。
しかし、三角形の問題で定理を使わない問題はほとんど無いので何か忘れている可能性があります。
そのためにも先ず図を描きましょう。

※
図を描くという作業の流れとしては同じなので、
\(\,tan15°\,\)のような記憶できない値の求め方も追加しておきます。

正弦定理と余弦定理を利用するとき、
特に正弦定理を使うときは
　\(\hspace{10pt}A+B+C=180^{\circ}\)
に注意しておく必要がありますよ。

正弦定理と余弦定理と面積

図形の問題を読み始めればだいたい分かりますが、
三角比の問題とわかったとき、使う定理や公式はだいたい３つです。

３つだけということではありません。
他にも使うことはありますが、基本となる定理は次の３つです。

正弦定理

外接円の半径を　\(R\)　とすると
　\(\displaystyle \color{red}{\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R}\)

余弦定理

第１もありますが、第２余弦定理だけで良いです。

　\(\color{red}{a^2=b^2+c^2-2\,b\,c\,\cos A}\)
　\(\color{red}{b^2=c^2+a^2-2\,c\,a\,\cos B}\)
　\(\color{red}{c^2=a^2+b^2-2\,a\,b\,\cos C}\)
または
　\(\displaystyle \cos A=\frac{b^2+c^2-a^2}{2\,b\,c}\)

　\(\displaystyle \cos B=\frac{c^2+a^2-b^2}{2\,b\,c}\)

　\(\displaystyle \cos C=\frac{a^2+b^2-c^2}{2\,b\,c}\)

これらは上の定理を変形したものですが覚えておくとはやいです。

面積の公式

　\(\displaystyle \color{red}{S=\frac{1}{2}\,bc \sin A}\)

　\(\displaystyle \color{red}{S=\frac{1}{2}\,ca \sin B}\)

　\(\displaystyle \color{red}{S=\frac{1}{2}\,ab \sin C}\)

これらの３つの公式、
　正弦定理、余弦定理、面積の公式
は使うものと考えて問題に取り組んで良い程です。

正弦定理を使うか余弦定理を使うか迷う問題

問題に角度が２つ与えられているので正弦定理か余弦定理だと考えを進めます。
角度が２つなら、普通は正弦定理ですね。
しかし、それがわかっていてもひっかかる問題があります。

例題

三角形\(\,\mathrm{ABC}\,\)において、
　\(\mathrm{\angle B=60^{\circ} , \angle C=75^{\circ} , BC=12}\)
のとき、
　\(\mathrm{AC}\hspace{4pt}\)の長さを求めよ。
また、三角形\(\,\mathrm{ABC}\,\)の外接円の半径を求めよ。

正弦定理と余弦定理の使い分けについては、

⇒　正弦定理と余弦定理を使い分ける問題の見分け方

でも説明していますが、おおよそ予想することは可能です。

しかし、この問題はそのままではどちらも使えません。
問題を良く見るとすぐに気がつくのですが、何かが足りていません。

「外接円」と書いてあるので正弦定理を使うにも、
与えられた角度では\(\,\sin 75^{\circ}\,\)の値もわからないし、
対辺もわかっていません。

余弦定理を使うにしても辺の長さが１つでは使えそうもありません。

何かが足りない。

不足している角度の大きさを解決する方法

何が足りていないかというと、「図」です。
図は必ず書いて考えるようにしましょう。

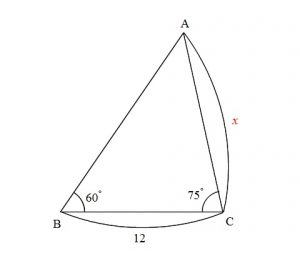
それでも問題になれていないと気がつきにくいのですが、
中学生でもわかる「三角形の内角の和」が使えていないことがあります。

この原因は、わかることは図に書き足す、という作業が足りていないだけです。
　「三角形の内角の和が\(\,180°\,\)」
になることを知っています。

この問題は「わからない」ではなくて「気がついていない」だけなのです。

　\(\begin{eqnarray}\mathrm{\angle A}&=&180^{\circ}-(60^{\circ}+75^{\circ})\\
&=&\color{red}{45^{\circ}}\end{eqnarray}\)

三角形で、２つの内角が与えられたらもう一つの内角もわかります。
落ち着けば、気がつけば当たり前、なのですが結構ひっかかりますね。

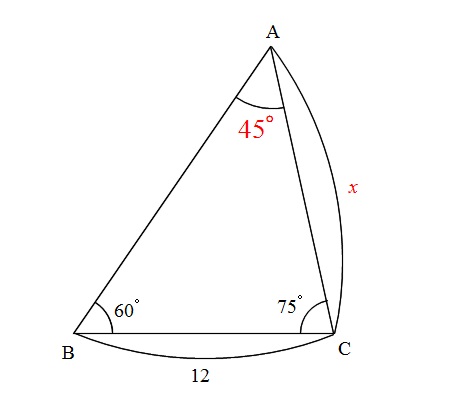
ここまでくれば正弦定理が使えるとすぐにわかります。

　\(\hspace{10pt}\displaystyle \frac{12}{\sin 45^{\circ}}=\frac{x}{\sin 60^{\circ}}\\
\Leftrightarrow 12\times \sin 60^{\circ}=\sin 45^{\circ}\times x\\
\displaystyle \Leftrightarrow 12\times \frac{\sqrt{3}}{2}=\frac{\sqrt{2}}{2}\times x\)

これから
　\(\hspace{10pt}x=6\sqrt{6}\\
\hspace{10pt}∴　\mathrm{AC}=\color{red}{6\sqrt{6}}\)

外接円の半径は
　\(\hspace{10pt}\displaystyle \frac{12}{\sin 45^{\circ}}=2R\)
または
　\(\hspace{10pt}\displaystyle \frac{6\sqrt{6}}{\sin 60^{\circ}}=2R\)
から
　\(R=\color{red}{6\sqrt{2}}\)
と求まります。

三角形の内角の和に気がつかなければ、アウト！です。
もったいないでしょう？

できるだけ図に情報を書き込みましょう。

tan15°の値の求め方

正弦定理や余弦定理とは別になりますが、
角度を図に示すことで求める応用問題を1つ追加しておきます。

よく見かける問題です。

「\(\,\tan 15^{\circ}\,\)の値を求めよ。」

改めていうことではないですが
　\(\hspace{10pt}\displaystyle \,\tan 15^{\circ}=\frac{1}{2}\,\tan30^{\circ}\,\)
ではありません。

角度の比と三角比の比は一致しませんよ。

図を利用します。
下図の様に三角定規と組合わせて\(\,15°\,\)を持つ直角三角形を書きます。

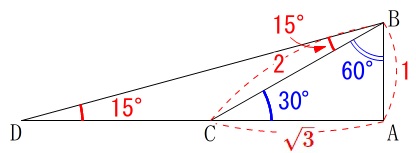
\(\,\mathrm{AB}\,\)を\(\,\color{red}{1}\,\)として線分比、
　\(\hspace{10pt}\mathrm{CB=\color{red}{2}\,,\,AC=\color{red}{\sqrt{3}}}\)
を書き込んであります。

このとき、\(\,\mathrm{△CBD}\,\)は二等辺三角形なので
　\(\hspace{10pt}\mathrm{DC=BC=\color{red}{2}}\)

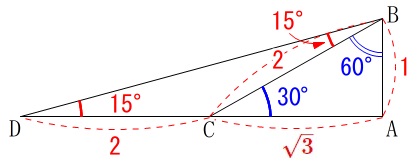
よって、
　\(\begin{eqnarray}\displaystyle
\tan 15^{\circ}&=&\mathrm{\frac{AB}{AD}}\\
&=&\frac{1}{2+\sqrt{3}}\\
&=&2-\sqrt{3}\end{eqnarray}\)