2019年度センター試験数学1Ａ第5問平面幾何問題の解説

2019年(平成31年）度に行われたセンター試験の数学１Ａ選択問題第5問の平面幾何問題の解説です。
第5問は内心の性質と余弦定理、チェバの定理が使えれば誘導を分かり易くしてくれているので得点しやすい問題です。
何より、問題用紙にスペースを大きく開けてくれているので図が書きやすく考えやすいです。

正解はセンターが発表していますので確認してください。

⇒　2019(H31)年センター試験数学1A問題

この問題は数学\(Ⅰ\mathrm{A}\)のみの部分掲載となります。

第\(\,5\,\)問（選択問題『平面幾何』）

問題文に与えられる条件を順番通りに処理していけば、自ずと答えが出るようになっています。

ただし、定義や定理はしっかり覚えておくことは必要です。

　\(\color{black}{\fbox{　条件　}}\)

\(\,\mathrm{△ABC}\,\)において
　\(\,\mathrm{AB=4　,　BC=4　,　AC=5}\,\)

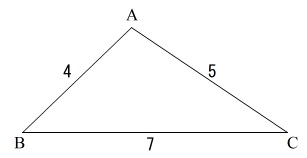
このとき
　\(\displaystyle \cos ∠\mathrm{BAC}=-\frac{1}{5}\)
　\(\displaystyle \sin ∠\mathrm{BAC}=\frac{2\sqrt{6}}{5}\)

と与えられています。

一応確認しておくと、余弦定理から
　\(\begin{eqnarray}\displaystyle
\cos \mathrm{A}&=&\frac{4^2+5^2-7^2}{2\times 4\times 5}\\
&=&\frac{16+25-49}{2\times 4\times 5}\\
&=&\frac{-8}{2\times 4\times 5}\\
&=&-\frac{1}{5}
\end{eqnarray}\)

また、\(\,\sin^2 \mathrm{A}+\cos^2 \mathrm{A}=1\,\)から
　\(\begin{eqnarray}\displaystyle
\sin^2&=&1-\cos^2 \mathrm{A}\\
&=&1-\left(-\frac{1}{5}\right)^2\\
&=&1-\frac{1}{25}\\
&=&\frac{24}{25}\\
\sin \mathrm{A}&=&\pm \frac{2\sqrt{6}}{5}
\end{eqnarray}\)
\(\,\mathrm{△ABC}\,\)においては\(\sin \mathrm{A}＞0\)なので
　\(\displaystyle \sin \mathrm{A}=\frac{2\sqrt{6}}{5}\)

これを問題に与えてくれています。
そのまま利用させてもらいましょう。
　『\(\,\mathrm{△ABC}\,\)の内接円の半径』
を聞かれています。

半径を求める前におおよその位置関係は確認しておきましょう。

　内接円は\(\,\mathrm{△ABC}\,\)の\(\,3\,\)辺が接線です。
　内接円の中心は3つの角の二等分線の交点です。

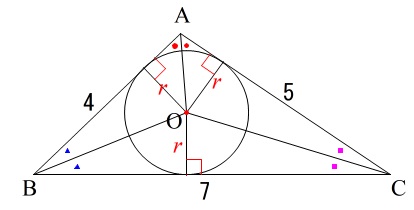
\(\,\mathrm{△ABC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\,\mathrm{AB}\cdot \mathrm{AC}\cdot \sin \mathrm{A}\\
&=&\frac{1}{2}\times 4\times 5\times \frac{2\sqrt{6}}{5}\\
&=&4\sqrt{6}
\end{eqnarray}\)

また内接円の半径\(\,\color{red}{r}\,\)を使って\(\,\mathrm{△ABC}\,\)の面積を表すと
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\,(\mathrm{AB+BC+CA})\,\color{red}{r}\\
&=&\frac{1}{2}(4+5+7)\,\color{red}{r}\\
&=&\frac{1}{2}\times 16\times \color{red}{r}\\
&=&8\,\color{red}{r}
\end{eqnarray}\)

これらの面積は等しいので
　\(\begin{eqnarray}\displaystyle
\,8\color{red}{r}&=&4\sqrt{6}\\
\color{red}{r}&=&\frac{4\sqrt{6}}{8}\\
&=&\frac{\sqrt{\color{black}{\fbox{\(\color{red}{　6　}\)}}}}{\color{black}{\fbox{\(\color{red}{　2　}\)}}}
\end{eqnarray}\)

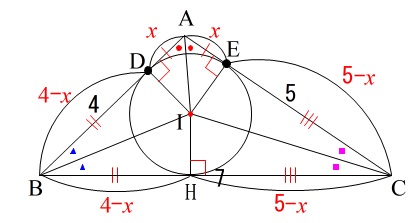
内心は角の二等分線の交点で、
内接円の半径は常に等しいことから合同な三角形を考えて、
　\(\,\mathrm{AD=AE\,,\,BD=BH\,,\,CE=CH}\,\)

\(\,\mathrm{AD=AE}=\color{red}{x}\,\)とすると
　\(\,\mathrm{BD=AB-AD}=\color{red}{4-x}\,\)
と表せるように
　\(\,\mathrm{CE}=\color{red}{5-x}\,\)

ここで
　\(\begin{eqnarray}
\mathrm{BC}&=&\mathrm{BH+CH}\\
&=&\mathrm{BD+CE}\\
&=&(\color{red}{4-x})+(\color{red}{5-x})\\
&=&9-2x
\end{eqnarray}\)

\(\,\mathrm{BC=7}\,\)なので
　\(\begin{eqnarray}
9-2x&=&7\\
-2x&=&7-9\\
x&=&1
\end{eqnarray}\)

よって\(\,\mathrm{AD}=\color{black}{\fbox{\(\,\color{red}{　1　}\,\)}}\,\)
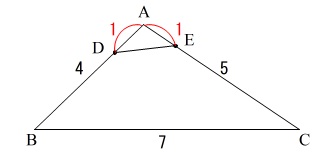また、余弦定理から
　\(\begin{eqnarray}
\mathrm{DE^2}&=&\mathrm{AD^2+AE^2-2AD}\cdot \mathrm{AE}\cdot \cos \mathrm{A}\\
&=&1^2+1^2-2\times 1\times 1\times \left(-\frac{1}{5}\right)\\
&=&1+1+\frac{2}{5}\\
&=&\frac{12}{5}
\end{eqnarray}\)

\(\,\mathrm{DE＞0}\,\)より
　\(\begin{eqnarray}
\mathrm{DE}&=&\frac{\sqrt{12}}{\sqrt{5}}\\
&=&\frac{2\sqrt{3}}{\sqrt{5}}\\
&=&\frac{\color{black}{\fbox{\(\,\color{red}{　2　}\,\)}}\sqrt{\color{black}{\fbox{\(\,\color{red}{　15　}\,\)}}}}{\color{black}{\fbox{\(\,\color{red}{　5　}\,\)}}}
\end{eqnarray}\)

条件が加わります。

　線分\(\,\mathrm{ＢＥ}\,\)と線分\(\,\mathrm{ＣＤ}\,\)の交点を\(\,\mathrm{P}\,\)
　線分\(\,\mathrm{ＡＰ}\,\)と辺\(\,\mathrm{ＢＣ}\,\)の交点を\(\,\mathrm{Q}\,\)
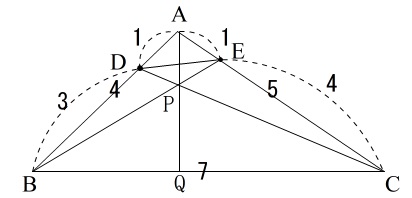チェバの定理より
　\(\begin{eqnarray}\displaystyle
\frac{\mathrm{BQ}}{\mathrm{QC}}\times \frac{\mathrm{CE}}{\mathrm{EA}}\times \frac{\mathrm{AD}}{\mathrm{DB}}&=&1\\
\frac{\mathrm{BQ}}{\mathrm{QC}}\times \frac{4}{1}\times \frac{1}{3}&=&1\\
\frac{\mathrm{BQ}}{\mathrm{QC}}&=&\frac{\color{black}{\fbox{\(\,\color{red}{　3　}\,\)}}}{\color{black}{\fbox{\(\,\color{red}{　4　}\,\)}}}
\end{eqnarray}\)

\(\,\mathrm{BC(=BQ+QC)}\,\)そのものの長さが\(\,7\,\)なので
　\(\,\mathrm{BQ:QC=3:4}\,\)
より
　\(\,\mathrm{BQ}=\color{black}{\fbox{\(\color{red}{　3　}\,\)}}\)

\(\,\mathrm{AD=1}\,\)と求まった後の線分の長さは
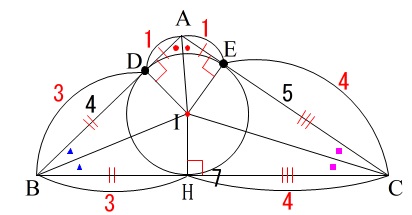このとき
　\(\,\mathrm{BH:HC=3:4}\,\)
でした。

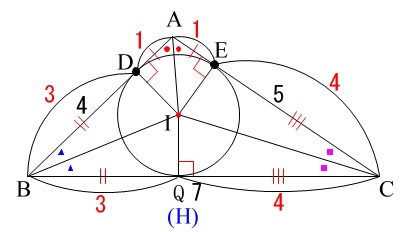
　\(\,\mathrm{BQ:QC=3:4}\,\)
で\(\,\mathrm{Q}\,\)と\(\,\mathrm{H}\,\)は一致するので\(\,\mathrm{IQ}\,\)は内接円の半径のことで
　\(\displaystyle \mathrm{IQ}=\frac{\sqrt{\color{black}{\fbox{\(\color{red}{　6　}\)}}}}{\color{black}{\fbox{\(\,\color{red}{　2　}\,\)}}}\)

ここで条件が加わります。

　直線\(\,\mathrm{CP}\,\)と\(\,\mathrm{△ABC}\,\)の内接円との交点で\(\,\mathrm{D}\,\)とは異なる点を\(\,\mathrm{F}\,\)
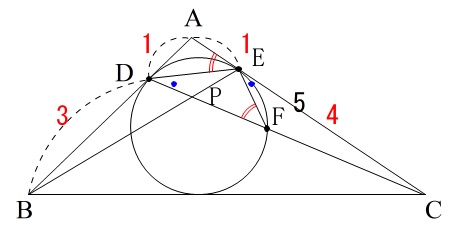接弦定理が使えます。
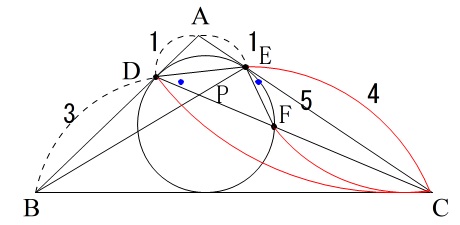方べきの定理でもいけそうですが、
\(\,\mathrm{DC,DF,EF}\,\)を求めるのがめんどうなので、接弦定理でいきます。笑

すでに\(\,\mathrm{DE}\,\)を求めているので

　\(\,\mathrm{∠\color{red}{DFE}=∠\color{blue}{AED}}\,\)
なので余弦定理から
　\(\begin{eqnarray}\displaystyle
\cos ∠\mathrm{\color{red}{DFE}}&=&\cos ∠\mathrm{\color{blue}{AED}}\\
&=&\frac{1^2+\left(\frac{2\sqrt{15}}{5}\right)^2-1^2}{2\times 1\times \frac{2\sqrt{15}}{5}}\\
&=&\frac{\frac{4\times 15}{25}}{\frac{4\sqrt{15}}{5}}\\
&=&\frac{4\times 15}{25}\times \frac{5}{4\sqrt{15}}\\
&=&\frac{3}{\sqrt{15}}\\
&=&\frac{3\sqrt{15}}{15}\\
&=&\frac{\sqrt{\color{black}{\fbox{\(\color{red}{　15　}\)}}}}{\color{black}{\fbox{\(\color{red}{　5　}\)}}}
\end{eqnarray}\)

この計算は余弦（コサイン）の定義に戻れば、

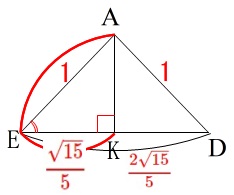
　\(\begin{eqnarray}\displaystyle
\cos ∠\mathrm{\color{red}{DFE}}&=&\frac{\mathrm{AE}}{\mathrm{EK}}\\
&=&\frac{\frac{\sqrt{15}}{5}}{1}\\
&=&\frac{\sqrt{\color{black}{\fbox{\(\color{red}{　15　}\)}}}}{\color{black}{\fbox{\(\color{red}{　5　}\)}}}
\end{eqnarray}\)