因数分解練習問題(高校数学Ⅱ)基本と応用46題

高校の数学Ⅱで扱う因数分解の基本から応用までの練習問題です。
因数分解は展開の逆演算です。
展開は乗法公式を覚えていなくても必ずできますが、因数分解は基本公式を覚えていないとできません。
応用となると少し手を加えないと先が見えない場合がありますので、ある程度のパターン問題を用意しておきました。

見るだけで無く自分で手を動かしてやってみて下さい。
計算力が無いと思っている人はきっと考えが変わります。

３次式以上の因数分解練習問題

利用するのは主に\(\,3\,\)次式の因数分解公式です。

　\(①\hspace{4pt}\color{red}{a^3+b^3=(a+b)(a^2-ab+b^2)}\)
　\(②\hspace{4pt}\color{red}{a^3+3a^2b+3ab^2+b^3=(a+b)^3}\)

上の公式で\(\,b\,\)の代わりに\(\,(-b)\,\)を入れた
　\(\hspace{4pt}\color{blue}{a^3-b^3}=\color{blue}{(a-b)(a^2+ab+b^2)}\)
および
　\(\hspace{4pt}\color{blue}{a^3-3a^2b+3ab^2-b^3}=\color{blue}{(a-b)(a^2-ab+b^2)}\)

この2つも断り無く利用します。

因数分解の基本的なことは数学\(\,Ⅰ\,,\,Ⅱ\,\)関係なくまとめてあります。

⇒　高校の因数分解公式一覧　たすき掛けや手順（やり方）

ここでは問題演習に集中しますので、思いっきり力をつけてください。

公式①を利用する因数分解問題（基本編）

公式通りに因数分解できる問題です。

(1)
　\(\hspace{10pt}x^3+8\\
=x^3+2^3\\
=\underline{　(x+2)(x^2-2x+4)　}\)

(2)
　\(\hspace{10pt}8x^3+27\\
=(2x)^3+3^3\\
=\underline{　(2x+3)(4x^2-6x+9)　}\)

(3)
　\(\hspace{10pt}x^3+8y^3\\
=x^3+(2y)^3\\
=\underline{　(x+2y)(x^2-2xy+4y^2)　}\)

(4)
　\(\hspace{10pt}8x^3+27y^3\\
=(2x)^3+(3y)^3\\
=\underline{　(2x+3y)(4x^2\color{red}{-6xy}+9y^2)　}\)

申し訳ありません。
因数分解後の符号が違っておりました。

次は符号が違う公式です。
　\(\color{blue}{a^3-b^3=(a-b)(a^2+ab+b^2)}\)

(5)
　\(\hspace{10pt}x^3-27\\
=x^3-3^3\\
=\underline{　(x-3)(x^2+3x+9)　}\)

(6)
　\(\hspace{10pt}27x^3-1\\
=(3x)^3-1^3\\
=\underline{　(3x-1)(9x^2+3x+1)　}\)

(7)
　\(\hspace{10pt}a^3-8b^3\\
=a^3-(2b)^3\\
=\underline{　(a-2b)(a^2+2ab+4b^2)　}\)

(8)
　\(\hspace{10pt}27a^3-125b^3\\
=(3a)^3-(5b)^3\\
=\underline{　(3a-5b)(9a^2+15ab+25b^2)　}\)

(1)から(8)は逆演算が展開公式に当てはまることより、
因数分解公式で因数分解できることの方が見抜きやすい問題ですね。

公式②を利用する因数分解問題（基本編）

公式
　\(\color{red}{a^3+3a^2b+3ab^2+b^3=(a+b)^3}\)
　\(\color{blue}{a^3-3a^2b+3ab^2-b^3=(a-b)^3}\)
がそのまま使える問題です。

先ず着目するのは\(\,3\,\)次の項と定数項が\(\,3\,\)乗されていることです。

(1)
　\(\hspace{10pt}x^3+3x^2+3x+1\\
=x^3+3(x)^2(1)+3(x)(1)^2+(1)^3\\
=\underline{　(x+1)^3　}\)

(2)
　\(\hspace{10pt}x^3-6x^2+12x-8\\
=\color{red}{x^3+3(x)^2(-2)+3(x)(-2)^2+(-2)^3}\\
=\underline{　(x-2)^3　}\)

または

　\(\hspace{10pt}x^3-6x^2+12x-8\\
=\color{blue}{x^3-3(x)^2(2)+3(x)(2)^2-(2)^3}\\
=\underline{　(x-2)^3　}\)

(3)
　\(\hspace{10pt}8x^3+12x^2+6x+1\\
=(2x)^3+3(2x)^2(1)+3(2x)(1)^2+(1)^3\\
=\underline{　(2x+1)^3　}\)

(4)
　\(\hspace{10pt}27x^3-54x^2+36x-8\\
=\color{red}{(3x)^3+3(3x)^2(-2)+3(3x)(-2)^2+(-2)^3}\\
=\underline{　(3x-2)^3　}\)

または

　\(\hspace{10pt}27x^3-54x^2+36x-8\\
=\color{blue}{(3x)^3-3(3x)^2(2)+3(3x)(2)^2-(2)^3}\\
=\underline{　(3x-2)^3　}\)

\(\,3\,\)次の項と定数項を確認したら「公式を使う」と\(\,2\,\)行目を飛ばしても良いですが、
「因数分解せよ。」という問題以外の式変形中だと、
因数分解できない場合もあるので確認しておいた方がいいです。

何を言っているのかわからない人もいるでしょうけど、
「因数分解せよ。」という問題はほぼ確実に因数分解できます。
（因数分解できるように問題が作られています。）

しかし、因数分解は多項式を整理するなどいろいろな場面で利用します。
その中で因数分解できるとは限らない場合もあるので、
安易に因数分解公式が使えると思い込まないように注意してください。

ここに取り上げた問題は全て因数分解できます。笑

因数分解基本総合問題

数学Ⅰから今までの練習のまとめ的な問題です。

基本的な見返り問題も含ませますので、
基本通り進めていけば必ず因数分解できる問題です。

２次式もあるので少しはなじみがあるでしょう。

(1)
　\(\hspace{10pt}-3a^3c+6a^2bc-3ab^2c\\
=-3ac(a^2-2ab+b^2)\\
=-\underline{　3(a-b)^2　}\)

共通因数を抜き出すことが因数分解の第１手順です。

(2)
　\(\hspace{10pt}(a+b)(x^2-y^2)-(x-y)(a^2-b^2)\\
=(\color{red}{a+b})(x+y)(\color{blue}{x-y})-(\color{blue}{x-y})(\color{red}{a+b})(a-b)\\
=(a+b)(x-y)\{(x+y)-(a-b)\}\\
=\underline{　(a+b)(x-y)(x+y-a+b)　}\)

部分的に因数分解すると共通因数が見えてきます。

(3)
　\(\hspace{10pt}4a^2-(1+a^2-b^2)^2\\
=(2a)^2-(1+a^2-b^2)^2\\
=\{\color{red}{2a+(1+a^2-b^2)}\}\{\color{blue}{2a-(1+a^2-b^2)}\}\\
=\color{red}{(a^2+2a+1-b^2)}\color{blue}{(b^2-a^2+2a-1)}\\
=\{\color{red}{(a+1)^2-b^2}\}\{\color{blue}{b^2-(a-1)^2}\}\\
=\color{red}{(a+1+b)(a+1-b)}\color{blue}{(b+a-1)(b-a+1)}\\
=\underline{　(a+b+1)(a-b+1)(a+b-1)(-a+b+1)　}\)

最初に全体を展開して、
どちらかの文字について整理しても良いです。

(4)
　\(\hspace{10pt}a^2+b^2+c^2+2bc-2ca-2ab\\
=a^2-(2ab+2ac)+(b^2+2bc+c^2)\\
=a^2-2(b+c)a+(b+c)^2\\
=\{a-(b+c)\}^2\\
=\underline{　(a-b-c)^2　}\)

最低次数の1つの文字について整理する、という基本通り処理しました。

公式
　\(\hspace{10pt}x^2+y^2+z^2+2xy+2yz+2zx\\
=(x+y+z)^2\)
に気がつけば、
　\(x=a\,,\,y=-b\,,\,z=-c\)
なので
　\(\hspace{10pt}a^2+b^2+c^2+2bc-2ca-2ab\\
=(a-b-c)^2\)

とすぐに因数分解できます。

(5)
　\(\hspace{10pt}a^6-64b^6\\
=(a^3)^2-(8b^3)^2\\
=(a^3+8b^3)(a^3-8b^3)\\
=(a+2b)(a^2-2ab+4b^2)(a-2b)(a^2+2ab+4b^2)\\
=\underline{　(a+2b)(a-2b)(a^2-2ab+4b^2)(a^2+2ab+4b^2)　}\)

公式
　\(\color{red}{x^2-y^2=(x+y)(x-y)}\)
を利用しました。

　\(\hspace{10pt}a^6-64b^6\\
=(a^2)^3-(4b^2)^3\)
と見ることもできますが、
この後に続く処理で説明しておきたい問題があるのでここでは省略します。

(6)
　\(\hspace{10pt}8a^3-12a^2b+6ab^2-b^3\\
=(2a)^3-3(2a)^2(b)+3(2a)(b)^2-(b)^3\\
=\underline{　(2a-b)^3　}\)

または
　\(\hspace{10pt}8a^3-12a^2b+6ab^2-b^3\\
=(2a)^3+3(2a)^2(-b)+3(2a)(-b)^2+(-b)^3\\
=\underline{　(2a-b)^3　}\)

これは公式通りです。

(7)
　\(\hspace{10pt}x^6+9x^3+8\\
=(x^3)^2+9(x^3)+8\\
=(x^3+1)(x^3+8)\\
=(x+1)(x^2-x+1)(x+2)(x^2-2x+4)\\
=(x+1)(x+2)(x^2-x+1)(x^2-2x+4)\)

与式は\(\,x^3=A\,\)とすると
　\(\hspace{10pt}A^2+9A+8\\
=(A+1)(A+8)\\
=(A+1^3)(A+2^3)\)
となるのでその後\(\,3\,\)次の因数分解公式を利用しています。

(8)
　\(\hspace{10pt}x^6-7x^3y^3-8y^6\\
=(x^3)^2-7(x^3)(y^3)-8(y^3)^2\\
=(x^3+y^3)(x^3-8y^3)\\
=(x+y)(x^2-xy+y^2)(x-2y)(x^2+2xy+4y^2)\\
=\underline{　(x+y)(x-2y)(x^2-xy+y^2)(x^2+2xy+4y^2)　}\)

これも
　\(x^3=a\,,\,y^3=b\)
と見ると与式を
　\(\hspace{10pt}a^2-7ab-8b^2\\
=(a+b)(a-8b)\)
とした後に\(\,3\,\)次の因数分解公式を用いています。

(9)
　\(\hspace{10pt}8a^6-9a^3+1\\
=(8a^3-1)(a^3-1)\\
=(2a-1)(4a^2+2a+1)(a-1)(a^2+a+1)\\
=\underline{　(2a-1)(a-1)(4a^2+2a+1)(a^2+a+1)　}\)

タスキガケの後に\(\,3\,\)次の因数分解公式を使っています。

与式で\(\,a^3=x\,\)とおいて
　\(\hspace{10pt}8x^2-9x+1\\
=(8x-1)(x-1)\)
と変形するのはそれほど不自然でもないでしょう。

変形が必要な因数分解の応用問題

因数分解の問題は因数分解できるよう作られています。
しかし、公式に直接当てはまらない場合が多いです。

因数分解応用問題１

少し変形することで公式が使えるようになるものも少なくないのでなれておきましょう。

ここまでは必ずできるようになっておいた方が良いです。

(1)
　\(\hspace{10pt}x^4+x^2+1\\
=(x^4+\color{red}{2x^2}+1)\color{red}{-x^2}\\
=(x^2+1)^2-x^2\\
=(x^2+1+x)(x^2+1-x)\\
=\underline{　(x^2+x+1)(x^2-x+1)　}\)

指数を偶数で変形して和と差の積の公式
　\(\color{red}{a^2-b^2=(a+b)(a-b)}\)
を利用する形です。
\(\,3\,\)行目が欲しい形ですが、\(\,2\,\)行目で係数を合わせています。
対称式変形でも似た作業があるのでなれれば簡単です。

(2)
　\(\hspace{10pt}a^4+3a^2+4\\
=(a^4+4a^2+4)-a^2\\
=(a^2+2)^2-a^2\\
=(a^2+2+a)(a^2+1-a)\\
=\underline{　(a^2+a+2)(a^2-a+1)　}\)

これを\(\,a^2\,\)の項の係数を\(\,3\,\)，定数項\(\,4\,\)にするために
　\(\hspace{10pt}a^4+3a^2+4\\
=(a^4\color{blue}{-4a^2}+4)\color{blue}{+7a^2}\\
=\color{red}{(a^2-2)^2}+7a^2\)
とすると和と差の積の公式は使えません。

少し手を動かしましょう。

(3)
　\(\hspace{10pt}x^4-11x^2+1\\
=(x^4\color{blue}{+2x^2}+1)^2\color{blue}{-13x^2}\)

違います。
無理数係数を許せば因数分解できますが、
有理数の係数の範囲に限って因数分解するのが普通です。

　\(\hspace{10pt}x^4-11x^2+1\\
=(x^4\color{red}{-2x^2}+1)\color{red}{-9x^2}\\
=(x^2-1)^2-(3x)^2\\
=(x^2-1+3x)(x^2-1-3x)\\
=\underline{　(x^2+3x-1)(x^2-3x-1)　}\)

(4)
　\(\hspace{10pt}a^4-8a^2+4\\
=(a^4\color{blue}{+4a^2}+4)\color{blue}{-12a^2}\\
=(a^2+2)^2-12a^2\)

違いますね。

　\(\hspace{10pt}a^4-8a^2+4\\
=(a^4\color{red}{-4a^2}+4)\color{red}{-4a^2}\\
=(a^2-2)^2-(2a)^2\\
=(a^2-2+2a)(a^2-2-2a)\\
=\underline{　(a^2+2a-2)(a^2-2a-2)　}\)

少しはなれましたか？
指数が偶数だけで成り立っている部分には注意しておきましょう。
（共通因数を抜き出した後にも注意しておきましょう。）

因数分解応用問題２

公式は使いますが元の式は\(\,3\,\)次式ではありません。
置きかえをせずに進めて見ますので確認してください。

(1)
　\(\hspace{10pt}a^6+b^6\\
=(a^2)^3+(b^2)^3\\
=(a^2+b^2)(a^4-a^2b^2+b^4)\)　

公式そのままなので\(\,3\,\)行目に公式確認の\(\,1\,\)行を入れていませんが、
不安な人は確認しておきましょう。

(2)
　\(\hspace{10pt}8x^6+27y^6\\
=(2x^2)^3+(3y^2)^3\\
=(2x^2+3y^2)\{(2x^2)^2-(2x^2)(3y^2)+(3y^2)^2\}\\
=\underline{　(2x^2+3y^2)(4x^4-6x^2y^2+9y^4)　}\)

「まだ因数分解できそう」という雰囲気で
　\(\hspace{10pt}4x^4-\color{blue}{6}x^2y^2+9y^4\\
=(2x^2-3y^2)^2\)
としてしまいそうですが、
　\(\hspace{10pt}(2x^2-3y^2)^2\\
=4x^4-\color{red}{12}x^2y^2+9y^4\)
なので因数分解できません。

(3)
　\(\hspace{10pt}x^6-y^6\\
=(x^2)^3-(y^2)^3\\
=(x^2-y^2)(x^4+3(x^2)^2(y^2)+y^4)\\
=(x+y)(x-y)(\color{red}{x^4+x^2y^2+y^4})　　･･･①\)

ただ、この問題はこれでは答えになっていません。
因数分解するときは有理数の範囲でできるところまで因数分解します。

確かに\(\,①\,\)は因数分解できてはいるのですが、
　\(\hspace{10pt}\color{red}{x^4+x^2y^2+y^4}\\
=x^4\color{blue}{+2x^2y^2}+y^4\color{blue}{-x^2y^2}\\
=(x^2+y^2)^2-x^2y^2\\
=(x^2+y^2)^2-(xy)^2\\
=(x^2+y^2+xy)(x^2+y^2-xy)\)

このようにまだ和と差の積の公式が使えます。

よって、
　\(\hspace{10pt}x^6-y^6\\
=\underline{　(x+y)(x-y)(x^2+y^2+xy)(x^2+y^2-xy)　}\)

これは「応用問題１」をやった後なら気がつくことができます。

または
　\(\hspace{10pt}x^6-y^6\\
=\color{magenta}{(x^3)^2-(y^3)^2}\\
=(x^3+y^3)(x^3-y^3)\\
=(x+y)(x^2-xy+y^2)(x-y)(x^2+xy+y^2)\\
=(x+y)(x-y)(x^2-xy+y^2)(x^2+xy+y^2)\)
のように「標準問題(5)」のように因数分解できます。

公式
　\(\color{red}{a^2-b^2=(a+b)(a-b)}\)
　\(\color{red}{a^3-b^3=(a-b)(a^2+ab+b^2)}\)
のどちらを先に使っているかの違いです。

標準問題(5)では
　\(\color{red}{a^2-b^2=(a+b)(a-b)}\)
を使って因数分解しました。
　\(\color{red}{a^3-b^3=(a-b)(a^2+ab+b^2)}\)
を使っても因数分解結果は同じになるはずです。

「標準問題(5)」の別解
　\(\hspace{10pt}a^6-64b^6\\
=(a^2)^3-(4b^2)^3\\
=(a^2-4b^2)\{(a^2)^2+(a^2)(4b^2)+(4b^2)^2)\}\\
=\{a^2-(2b)^2\}\{(a^2+4b^2)^2-4a^2b^2\}\\
=\{a^2-(2b)^2\}\{(a^2+4b^2)^2-(2ab)^2\}\\
=(a+2b)(a-2b)(a^2+4b^2+2ab)(a^2+4b^2-2ab)\\
=(a+2b)(a-2b)(a^2+2ab+4b^2)(a^2-2ab+4b^2)\)

結果が同じになっているか確認しておいてください。

つまり、標準問題(5)の時点で
　\(\hspace{10pt}a^6-64b^6\\
=(a^2)^3-(4b^2)^3\\
=(a^2-4b^2)\{(a^2)^2+(a^2)(4b^2)+(4b^2)^2)\}\\
=(a+2b)(a-2b)(a^4+4a^2b^2+16b^4)\)
まで因数分解できた人は、「おしい！」状態だった訳です。
もう一歩先があったんですね。

(4)
　\(\hspace{10pt}27a^6-8b^6\\
=(3a^2)^3-(2b^2)^3\\
=(3a^2-2b^2)\{(3a^2)^2+(3a^2)(2b^2)+(2b^2)^2\}\\
=(3a^2-2b^2)(9a^4+6a^2b^2+4b^4)\)

今までの流れからすると
　\(9a^4+6a^2b^2+4b^4\)
がまだ因数分解できそうですよね。
しかし、
　\(\hspace{10pt}9a^4+6a^2b^2+4b^4\\
=(3a^2+2b^2)^2+2a^2b^2\\
=(3a^2-2b^2)2+10a^2b^2\)
なので有理数係数では因数分解できません。

「まぎらわしい！」と思った人がいると思います。笑
申し訳ないです。
しかし、実際にはレベル順に問題が並んでいるわけではありません。
可能性を試すという作業は自分でやらないといけないのです。

(5)
　\(\hspace{10pt}8a^3-6a^2+3a-1\\
=\color{red}{8a^3-1}-\color{blue}{6a^2+3a}\\
=\color{red}{(8a^3-1)}-\color{blue}{3a(2a-1)}\\
=\color{red}{(2a-1)(4a^2+2a+1})-\color{blue}{3a(2a-1)}\\
=(2a-1)(\color{red}{4a^2+2a+1}-\color{blue}{3a})\\
=\underline{　(2a-1)(4a^2-a+1)　}\)

因数定理を使えば応用でもありませんが、
組合わせる順番で共通因数を見つけるという中学のときにやっていたような方法です。

次の問題につなげるために1つだけ取り入れておきました。

工夫が必要な因数分解応用問題

展開のときと同様に計算順序の工夫が大きな差となる問題や、
タスキガケを複雑にこなす問題もあります。

ここからが因数分解の本番です。

(1)
　\(\hspace{10pt}x(\color{red}{x+1})(\color{blue}{x+2})(\color{magenta}{x+3})+1\\
=x(\color{magenta}{x+3})(\color{red}{x+1})(\color{blue}{x+2})+1\\
=(x^2+3x)(x^2+3x+2)+1\\
=(x^2+3x)^2+2(x^2+3x)+1\\
=\underline{　(x^2+3x+1)^2　}\)

\(\,3\,\)行目で\(\,x^2+3x=A\,\)とすれば
　\(\hspace{10pt}A(A+2)+1\\
=A^2+2A+1\\
=(A+1)^2\)
となって見やすくなります。

いずれにしても\(\,x^2+3x\,\)という共通部分を作るように組み合わせを考えます。
瞬間で、一回で見つかるとは限りません。

公式に当てはめるだけの問題が入試問題になるなんて少ないです。
　手を動かせ！
　実験しろ！
　試せ！
　作業しろ！
　
あ、皆様にいっているわけではありませんよ。
見てるか？君だよ、君！！

それと、
因数分解なんて数式扱っていると忘れがちになるけど、
単語を覚えることを忘れないこと。

数学は言語科目です。

『人は忘れる生き物だということを忘れるな！』
この矛盾をどう解く？

ここまで読んでくれているのは塾生くらいだろうから偉そうに説教しておきました。笑
（毎回いってることだけど）

先に進みましょう。

(2)
　\(\hspace{10pt}2a^2-5ab-3b^2+a+11b-6\\
=2a^2+(-5b+1)a-3b^2+11b-6\\
=2a^2+(-5b+1)a-(\color{red}{3b^2-11b+6})\\
=\color{blue}{2a^2+(-5b+1)a-(b-3)(3b-2)}\\
=\{2a+(b-3)\}\{a-(3y-2)\}\\
=\underline{　(2a+b-3)(a-3b+2)　}\)

タスキガケを二回行っています。

一回目は
　\(\color{red}{3b^2-11b+6}\)
において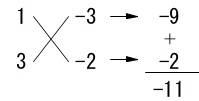　\(\hspace{10pt}\color{red}{3b^2-11b+6}\\
=(b-3)(3b-2)\)

二回目は
　\(\color{blue}{2a^2+(-5b+1)a-(b-3)(3b-2)}\)
において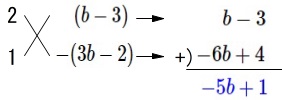　\(\hspace{10pt}\color{blue}{2a^2+(-5b+1)a-(b-3)(3b-2)}\\
=\{2a+(b-3)\}\{a-(3y-2)\}\)

文字式を係数に持つタスキガケもたくさん出てきますので、
確実にできるようにしておきましょう。

(3)
　\(\hspace{10pt}x^2+xy-2y^2+2x+7y-3\\
=x^2+(y+2)x-2y^2+7y-3\\
=x^2+(y+2)x-(2y^2-7y+3)\\
=x^2+(y+2)x-(2y-1)(y-3)\\
=(x+2y-1)\{x-(y-3)\}\\
=\underline{　(x+2y-1)(x-y+3)　}\)

最低次数の文字で整理してタスキガケ因数分解です。
\(\,y\,\)で整理しても良いですが、
係数が\(\,1\,\)の\(\,x\,\)で整理する方が楽です。

これは基本問題ですが、
後に続くややこしい因数分解のための練習です。

(4)
　\(\hspace{10pt}a^2b+b^2\color{red}{c}-b^3-a^2\color{red}{c}\\
=(b^2-a^2)\color{red}{c}+a^2b-b^3\\
=(b^2-a^2)c+b(a^2-b^2)\\
=-(a^2-b^2)c+(a^2-b^2)c\\
=(a^2-b^2)(b-c)\\
=\underline{　(a+b)(a-b)(b-c)　}\)

最低次数の\(\,c\,\)で整理して共通因数を抜き出しました。

\(\,4\,\)行目以降は
　\(\hspace{10pt}(b^2-a^2)c+b(a^2-b^2)\\
=(b^2-a^2)c-(b^2-a^2)b\\
=(b^2-a^2)(c-b)\\
=(b+a)(b-a)(c-b)\)
でも良いですよ。

他にも
　\(\hspace{10pt}\color{blue}{a^2b}\color{magenta}{+b^2c-b^3}\color{blue}{-a^2c}\\
=\color{blue}{a^2b-a^2c}\color{magenta}{-b^3+b^2c}\\
=a^2(b-c)-b^2(b-c)\\
=(a^2-b^2)(b-c)\\
=(a+b)(a-b)(b-c)\)
と偶然因数分解できることもあります。
しかし、
最低次数の文字で整理すると、
必ず定数項が因数分解できるはずなので、
次数が違う場合は最低次数の文字で整理することをおすすめします。

次は対称式なのでどの文字でも次数が同じです。
つまり、何でも良いということですが、
着目した文字以外は定数扱いすることを忘れないように変形すると進めやすいです。

(5)
　\(\hspace{10pt}(a+b)(b+c)(c+a)+abc\\
=(b+c)\{(a+b)(c+a)\}+abc\\
=(b+c)\{a^2+(b+c)a+bc\}+abc\\
=\color{red}{(b+c)a^2+\{(b+c)^2+bc\}a+bc(b+c)}\\
=\color{red}{\{a+(b+c)\}\{(b+c)a+bc\}}\\
=\underline{　(a+b+c)(ab+bc+ca)　}\)

\(\,4,5\,\)行目はタスキガケ因数分解です。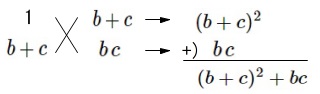文字係数のタスキガケにもなれておきましょう。

次も\(\,a,b\,\)どちらも同じ次数です。
\(\,a\,\)について整理していくことにします。

(6)
　\(\hspace{10pt}(ab+1)(a+1)(b+1)+ab\\
=(b+1)\color{blue}{(ab+1)(a+1)}+ab\\
=(b+1)\{\color{blue}{ba^2+(b+1)a+1}\}+ab\\
=b(b+1)a^2+(b+1)^2a+ab+(b+1)\\
=\color{red}{b(b+1)a^2+\{(b+1)^2+b\}a+(b+1)}\\
=\color{red}{\{ba+(b+1)\}\{(b+1)a+1\}}\\
=\underline{　(ab+b+1)(ab+a+1)　}\)

\(\,5,6\,\)行目はタスキガケ因数分解です。
(5)と同じように自分で試して見てください。

　\(\color{red}{b(b+1)}a^2+\{(b+1)^2+b\}a+\color{blue}{(b+1)}\)
のタスキガケ因数分解の組み合わせは
　\(\color{red}{b}\times \color{blue}{(b+1)}+\color{red}{(b+1)}\times \color{blue}{1}\)
　\(\color{red}{b}\times \color{blue}{1}+\color{red}{(b+1)}\times \color{blue}{(b+1)}\)
　\(\color{red}{b(b+1)}\times \color{blue}{1}+\color{red}{1}\times \color{blue}{(b+1)}\)
　\(\color{red}{b(b+1)}\times \color{blue}{(b+1)}+\color{red}{1}\times \color{blue}{1}\)
のどれかです。
（自分でやってみないとながめていても分かりませんよ。）
\(\,1\,\)という因数はどの因数にもあることを忘れないようにしましょう。

項の組み合わせで工夫する因数分解

因数分解はやることは決まっていますが、
ここからは多少の変形が必要になるので、
自力で解けるようになるためには手を動かすしかありません。

(1)
　\(\hspace{10pt}x^5+x^4+x^3+x^2+x+1\\
=x^5+x^2+x^4+x+x^3+1\\
=x^2(\color{red}{x^3+1})+x(\color{red}{x^3+1})+(\color{red}{x^3+1})\\
=(x^3+1)(x^2+x+1)\\
=\underline{　(x+1)(x^2-x+1)(x^2+x+1)　}\)

部分的にでも因数分解できるところがあったので、
共通因数に\(\,\color{red}{x^3+1}\,\)ができるように順序を入れかえて見ました。

　\(\hspace{10pt}x^5+x^4+x^3+x^2+x+1\\
=(x^5+x^4+x^3)+(x^2+x+1)\\
=x^3(\color{blue}{x^2+x+1})+(\color{blue}{x^2+x+1})\\
=(x^3+1)(x^2+x+1)\\
=(x+1)(x^-x+1)(x^2+x+1)\)

次数が規則的に変わっているので、
係数が同じであることに着目しておけば、
項数をそろえてまとめて見るのもいいです。
（こっちの方がきれいですね。）

　\(\hspace{10pt}x^5+x^4+x^3+x^2+x+1\\
=x^4(\color{magenta}{x+1})+x^2(\color{magenta}{x+1})+(\color{magenta}{x+1})\\
=(x+1)(x^4+x^2+1)\\
=(x+1)\{(x^2+1)^2-x^2\}\\
=(x+1)(x^2+1+x)(x^2+1-x)\\
=(x+1)(x^2+x+1)(x^2-x+1)\)

ここまで来れば共通因数を\(\,\color{magenta}{x+1}\,\)と見ても、
この因数分解に違和感はないでしょう。

(2)
　\(\hspace{10pt}(a^2-1)(b^2-1)+4ab\\
=a^2b^2-a^2-b^2+1+4ab\\
=(b^2-1)a^2+4ba-(b^2-1)\\
=(b+1)(b-1)a^2+4ba+(b+1)(b-1)\\
=\{\color{blue}{(b-1)a+(b+1)}\}\{\color{red}{(b+1)a-(b-1)}\}\\
=(ab-a+b+1)(ab+a-b+1)\)

少し見にくいタスキガケですが、
できなくはないでしょう。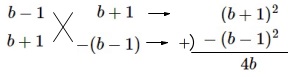次数が同じだったので手順通りに\(\,a\,\)について整理し、
タスキガケ因数分解で処理しました。

展開して気がついた方法もあります。

　\(\hspace{10pt}(a^2-1)(b^2-1)+4ab\\
=a^2b^2-a^2-b^2+1+\color{red}{4ab}\\
=a^2b^2\color{red}{+2ab}+1-a^2-b^2\color{red}{+2ab}\\
=(a^2b^2+2ab+1)-(a^2-2ab+b^2)\\
=(ab+1)^2-(a-b)^2\\
=\{(ab+1)+(a-b)\}\{(ab+1)-(a-b)\}\\
=(ab+a-b+1)(ab-a+b+1)\)

和と差の積の公式
　\(\color{blue}{x^2-y^2=(x+y)(x-y)}\)
を利用しましたが、
この\(\,\color{red}{4ab}\,\)を2つに分けるのはよく使う方法です。

もちろん、\(\,b\,\)について整理しても同じ結果になります。
やってみてください。（自分で。笑）

(3)
　\(\hspace{10pt}a^4\color{red}{-7a^2b^2}+b^4\\
=a^4\color{red}{+2a^2b^2}+b^4\color{red}{-9a^2b^2}\\
=(a^2+b^2)^2-(3ab)^2\\
=(a^2+b^2+3ab)(a^2+b^2-3ab)\\
=\underline{　(a^2+3ab+b^2)(a^2-3ab+b^2)　}\)

応用問題１の見直しです。

　\(\hspace{10pt}a^4\color{red}{-7a^2b^2}+b^4\\
=a^4\color{red}{-2a^2b^2}+b^4\color{red}{-5a^2b^2}\)
とすると和と差の積の公式が使えないので、
やってみるしか無いです。

この形は見慣れたと思うので先に進みます。

(4)
　\(\hspace{10pt}x^8+x^4y^4+y^8\\
=x^8\color{blue}{+2x^4y^4}+y^8\color{blue}{-x^4y^4}\\
=(x^4+y^4)^2-(x^2y^2)^2\\
=\color{red}{(x^4+y^4+x^2y^2)(x^4+y^4-x^2y^2)}\\
=\{(x^2+y^2)^2-x^2y^2\}(x^4-x^2y^2+y^4)\\
=\underline{　(x^2+xy+y^2)(x^2-xy+y^2)(x^4-x^2y^2+y^4)　}\)

これも同じ形ですが\(\,4\,\)行目で終わりではありません。

普通は有理数の範囲で因数分解しますが、
この問題を無理数の範囲まで係数を許して因数分解すると、
3つめの因数は
　\(\hspace{10pt}x^4-x^2y^2+y^4\\
=x^4\color{magenta}{+2x^2y^2}+y^4\color{magenta}{-3x^2y^2}\\
=(x^2+y^2)^2-(\sqrt{3}xy)^2\\
=(x^2+\sqrt{3}xy+y^2)(x^2-\sqrt{3}xy+y^2)\)
となります。

無理数や複素数の範囲までの因数分解は、指定が無い限りしなくて良いです。
また、「係数」が無理数や複素数の範囲までという意味になります。

(5)
　\(\hspace{10pt}a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2\\
=a^4-2(b^2+c^2)a^2+\color{magenta}{b^4+c^4-2b^2c^2}\\
=a^4-2(b^2+c^2)a^2+(b^2-c^2)^2\\
=a^4-2(b^2+c^2)a^2+\{(b+c)(b-c)\}^2\\
=a^4-2(b^2+c^2)a^2+\color{red}{(b+c)^2}\color{blue}{(b-c)^2}\\
=\{a^2-\color{red}{(b+c)^2}\}\{a^2-\color{blue}{(b-c)^2}\}\\
=\underline{　(a+b+c)(a-b-c)(a+b-c)(a-b+c)　}\)

手順通り文字を\(\,a\,\)について整理して他を定数と見たとき、
　\(\color{magenta}{b^4+c^4-2b^2c^2}\)
が平方式になったのでタスキガケ因数分解するとうまく行きました。

途中から係数と定数項に着目して変形して見ると、
今までの総復習のような変形が通用します。

　\(\hspace{10pt}a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2\\
=a^4-2(b^2+c^2)a^2+\color{magenta}{b^4+c^4-2b^2c^2}\\
=a^4-2(b^2+c^2)a^2+\color{magenta}{(b^2+c^2)^2-4b^2c^2}\\
=\color{red}{a^4-2(b^2+c^2)a^2+(b^2+c^2)^2}-\color{blue}{4b^2c^2}\\
=\color{red}{\{a^2-(b^2+c^2)\}^2}-\color{blue}{(2bc)^2}\\
=\{a^2-(b^2+c^2)+2bc\}\{a^2-(b^2+c^2)-2bc\}\\
=\{a^2-(b^2-2bc+b^2)\}\{a^2-(b^2+2bc+b^2)\}\\
=\{a^2-(b-c)^2\}\{a^2-(b+c)^2\}\\
=(a+b-c)(a-b+c)(a+b+c)(a-b-c)\)

\(\,4,5\,\)行目で平方の差を作り、
和と差の積の公式が使えるように変形しました。

ただ、因数分解の手順通りでほとんどは因数分解はできる、
というのは感じておいて欲しいところです。

次は手順度下りに進めても少し工夫が必要です。
このような嫌らしい問題は、誰が考えるんでしょうね。笑

出題者には経験という大きな土台がありますが、
普通の高校生にとってはハードル高くないですか？

出題する人は受験という限られた機会で、
進学先で通用するかどうかの判断をしなくてはならないので、
難関校受験者は覚悟が必要ですよ。

ちなみに、共通テストであればここまででついてきた人は十分に通用します。
（たぶん、だけど笑笑）

(6)
　\(\hspace{10pt}x^4+2x^2-4xy-y^2+9\\
=-y^2-4xy+x^4\color{red}{+2x^2}+9\\
=-y^2-4xy\color{red}{-4x^2}+x^4\color{red}{+6x^2}+9\\
=-(y^2+4xy+4x^2)+(x^4+6x^2+9)\\
=-(y+2x)^2+(x^2+3)^2\\
=(x^2+3)^2-(y+2x)^2\\
=\{(x^2+3)+(y+2x)\}\{(x^2+3)-(y+2x)\}\\
=(x^2+3+y+2x)(x^2+3-y-2x)\\
=\underline{　(x^2+2x+y+3)(x^2-2x-y+3)　}\)

次数の低い\(\,y\,\)で整理した後、
定数項が因数分解できるように
　\(\color{red}{2x^2}=\color{red}{-4x^2}+\color{red}{6x^2}\)
と変形しました。

定数項を因数分解するだけなら
　\(\color{red}{2x^2}=\color{blue}{-8x^2}+\color{blue}{10x^2}\)
と変形して、
　\(\hspace{10pt}-y^2-4xy+x^4\color{red}{+2x^2}+9\\
=-y^2-4xy\color{blue}{-8x^2}+x^4\color{blue}{+10x^2}+9\\
=-(y^2+4xy+8x^2)+(x^2+1)(x^2+9)\)
とすることや、
　\(\color{red}{2x^2}=\color{magenta}{+12x^2}\color{magenta}{-10x^2}\)
と変形して、
　\(\hspace{10pt}-y^2-4xy+x^4\color{red}{+2x^2}+9\\
=-y^2-4xy\color{magenta}{+12x^2}+x^4\color{magenta}{-10x^2}+9\\
=-(y^2+4xy-12x^2)+(x^2-1)(x^2-9)\)
とすることもできますが、
あまりにも先が見えてこないのでやめます。

ところで、
　　\(\color{red}{2x^2}=\color{red}{-4x^2}+\color{red}{6x^2}\)
が見えた時点で気がつくことですが、
　\(\hspace{10pt}x^4+2x^2-4xy-y^2+9\\
=x^4\color{red}{+6x^2}+9-y^2-4xy\color{red}{-4x^2}\\
=(x^4+6x^2+9)-(y^2+4xy+4x^2)\\
=(x^2+3)^2-(y+2x)^2\\
=\{(x^2+3)+(y+2x)\}\{(x^2+3)-(y+2x)\}\\
=(x^2+2x+y+3)(x^2-2x-y+3)\)

このように工夫できれば次数の低い文字を気にしなくても因数分解できます。

ここでは関係ありませんが、
「\(\,x^4+2x^2-4xy-y^2+9≦0\,\)を満たす領域を図示せよ。」
と発展させることができる因数分解問題です。

公式として覚えておきたい因数分解の手順

対称式、交代式を利用して因数分解する方法も解説に加えておきました。

よく見かける因数分解で、
公式として紹介もしてあるので覚えている人もいると思います。

ここでは公式を暗記するためでは無く、
因数分解する課程を再度確認しておいてください。

(1)
　\(\hspace{10pt}a^3+b^3+c^3-3abc\\
=a^3-3bca+b^3+c^3\\
=a^3-3bca+(b+c)(b^2-bc+c^2)\)

次数が同じなので\(\,a\,\)について整理してみましたが、
うまくいく方法が見えてきません。

部分的に因数分解することを考えると、
　\(\hspace{10pt}a^3+b^3\\
=(a+b)(a^2-ab+b^2)\)
ですが、やはりうまくいきません。

\(\,a^3+b^3+c^3\,\)を作るために、
　\(\,(a+b+c)\,\)と\(\,(a^2+b^2+c^2)\,\)の積
を計算すると
\(\hspace{10pt}(a+b+c)(a^2+b^2+c^2)\\
=a^3+b^3+c^3\\
\hspace{10pt}+a(b^2+c^2)+b(a^2+c^2)+c(a^2+b^2)\)
なので移項して
　\(\hspace{10pt}a^3+b^3+c^3\\
=(a+b+c+)(a^2+b^2+c^2)\\
\hspace{14pt}-a(b^2+c^2)-b(a^2+c^2)-c(a^2+b^2)\)

両辺に\(\,\color{red}{-3abc}\,\)を加えて
　\(\hspace{10pt}a^3+b^3+c^3\color{red}{-3abc}\\
=(a+b+c+)(a^2+b^2+c^2)\\
\hspace{10pt}\color{blue}{-a(b^2+c^2)-b(a^2+c^2)-c(a^2+b^2)}\color{red}{-3abc}\)

部分的に\(\,a\,\)について整理して見ると
　\(\hspace{10pt}\color{blue}{-a(b^2+c^2)-b(a^2+c^2)-c(a^2+b^2)}\color{red}{-3abc}\\
=-\{(b+c)a^2+(b^2+c^2+3bc)a+bc(b+c)\}\\
=-\{(b+c)a+bc\}\{a+(b+c)\}\\
=-(ab+bc+ca)(a+b+c)\)

タスキガケを使って因数分解できました。
これは全体に共通因数があることを示しています。

　\(\hspace{10pt}a^3+b^3+c^3-3abc\\
=(a+b+c)(a^2+b^2+c^2)\\
\hspace{10pt}-(a+b+c)(ab+bc+ca)\\
=\underline{　(a+b+c)(a^2+b^2+c^2-ab-bc-ca)　}\)

おなじみの公式です。笑

手順通りに進めて行くために変形を考えていくと因数分解できます。

しかし、
この因数分解（公式の証明）には対称式変形を利用するときれいです。

　\(\hspace{10pt}\color{blue}{x^3+y^3=(x+y)^3-3xy(x+y)}\)

これを\(\,2\,\)回利用すると
　\(\hspace{10pt}\color{red}{a^3+b^3}+c^3-3abc\\
=\color{red}{(a+b)^3-3ab(a+b)}+c^3-3abc\\
=\color{blue}{(a+b)^3+c^3}-3ab(a+b)-3abc\\
=\color{blue}{\{(a+b+c)^3-3(a+b)c(a+b+c)\}}\\
\hspace{10pt}-3ab(a+b+c)\\
=(a+b+c)\{(a+b+c)^2-3(a+b)c-3ab\}\)

ここで後半（2つ目の因数）だけを別で計算すると
　\(\hspace{10pt}(a+b+c)^2-3(a+b)c-3ab\\
=a^2+b^2+c^2\color{red}{+2ab}+\color{blue}{2bc}\color{magenta}{+2ca}\\
\hspace{30pt}\color{magenta}{-3ac}\color{blue}{-3bc}\color{red}{-3ab}\\
=a^2+b^2+c^2-ab-ba-ca\)
なので
　\(\hspace{10pt}a^3+b^3+c^3-3abc\\
=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)

もう少し変化を加えて、
　基本対称式変形
　\(\hspace{10pt}\color{blue}{x^3+y^3=(x+y)^3-3xy(x+y)}\)
　因数分解
　\(\hspace{10pt}\color{magenta}{x^3+y^3=(x+y)(x^2-xy+y^2)}\)
の両方を利用すると
　\(\hspace{10pt}a^3+b^3+c^3-3abc\\
=\color{red}{(a+b)^3-3ab(a+b)}+c^3-3abc\\
=\color{magenta}{(a+b)^3+c^3}-3ab(a+b)-3abc\\
=(a+b+c)\{(a+b)^2-(a+b)c+c^2\}\\
\hspace{10pt}-3ab(a+b+c)\\
=(a+b+c)\{\color{blue}{(a+b)^2-(a+b)c+c^2-3ab}\}\\
=\underline{　(a+b+c)(a^2+b^2+c^2-ab-bc-ca)　}\)

\(\,5\,\)行目二つ目の因数の計算は飛んでいます。
　\(\hspace{10pt}\{\color{blue}{(a+b)^2-(a+b)c+c^2-3ab}\}\\
=a^2+2ab+b^2-ac-bc+c^2-3ab\\
=a^2+b^2+c^2-ab-bc-ca\)
自分で行間をうめておいて下さい。

今さらこの公式を証明するような問題は出ないと思いますが、
基本対称式変形を利用すると（割と？）きれいだった、
と覚えておくと良いです。

そうで無ければ相当な無駄な時間をこの因数分解にかけることになりますよ。

\(\color{red}{\fbox{　公式　}}\)
　\(\hspace{10pt}\color{red}{a^3+b^3+c^3-3abc}\\
\color{red}{=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)}\)

公式なので証明無しに使って良いです。
ただし、それなりの大学入試でしか使いません。

ついでに言っておきますが、
対称式は因数分解したときに、基本対称式の組み合わせで表すことができます。
そのことを利用しても因数分解することができますよ。

後はサクッとできる因数分解なのでさっさと済ませてしまいましょう。
そもそも、まだ読んでいる人いる？ｗｗ

ここまで手を動かしながら自分で確認してきたなら、
数学\(\,Ⅲ\,\)を除けば十分な「計算力」は着いていると断言できます。

そして、ここまで自分で手を動かしたことを数学\(\,Ⅲ\,\)でも続ければ、
数学は受験で大きな武器になっていること間違いなし！

後やることは「作業」を続けることだけです。

いやあ、疲れた。
これを言ういうためにどれだけ時間かかったんだろう。
モニターの文字が霞んで見える。

(2)
　\(\hspace{10pt}(x+y+z)^3-x^3-y^3-z^3\)

展開すると\(\,x^3\,,\,y^3\,,\,z^3\,\)は消えるので
　\((x+y+z)^3\)
を展開しておきましょう。

展開公式
　\(\color{blue}{(a+b)^3=a^3+3a^2b+3ab^2+b^3}\)
を\(\,2\,\)回使います。

　\(\hspace{10pt}(\color{red}{x+y}+\color{blue}{z})^3\\
=\color{red}{(x+y)^3}+3\color{red}{(x+y)^2}\color{blue}{z}+3\color{red}{(x+y)}\color{blue}{z^2}+\color{blue}{z^3}\\\\
=\color{magenta}{(x+y)^3}+3(x+y)z(x+y+z)+z^3\\
=\color{magenta}{x^3+3x^2y+3xy^2+y^3}\\
\hspace{10pt}+3(x+y)z(x+y+z)+z^3\\
=x^3+y^3+z^3\\
\hspace{10pt}+3xy(x+y)+3(x+y)z(x+y+z)\\
=x^3+y^3+z^3\\
\hspace{10pt}+3(x+y)(\color{red}{xy+zx+zy+z^2})\\
=x^3+y^3+z^3\\
\hspace{10pt}+3(x+y)\{\color{red}{(y+z)x+(y+z)z)}\}\\
=x^3+y^3+z^3\\
\hspace{10pt}+3(x+y)(y+z)(z+x)\)

よって
　\(\hspace{10pt}(x+y+z)^3-x^3-y^3-z^3\\
=\underline{　3(x+y)(y+z)(z+x)　}\)

展開の練習問題でチラッと紹介した公式です。

ところで与式は
　\(\hspace{10pt}(x+y+z)^3-(x^3+y^3+z^3)\)
なので基本対称式変形を利用して
　\(\hspace{10pt}\color{red}{x^3+y^3}+z^3\\
=\color{red}{(x+y)^3-3xy(x+y)}+z^3\\
=\color{blue}{(x+y)^3+z^3}\\
\hspace{10pt}-3xy(x+y)\\
=\color{blue}{(x+y+z)^3-3(x+y)z(x+y+z)}\\
\hspace{10pt}-3xy(x+y)\)
と変形できるので
　\(\hspace{10pt}(x+y+z)^3-x^3-y^3-z^3\\
=3(x+y)z(x+y+z)+3xy(x+y)\\
=3(x+y)\{z(x+y+z)+xy\}\\
=3(x+y)(zx+zy+z^2+xy)\\
=3(x+y)\{(y+z)x+(y+z)z\}\\
=3(x+y)(y+z)(z+x)\)

(1)の公式を導いたときと同じ基本対称式変形の後の因数分解です。

(3)
　\(\hspace{10pt}a^2(b-c)+b^2(c-a)+c^2(a-b)\\
=(b-c)a^2\color{blue}{+b^2c}\color{red}{-b^2a+c^2a}\color{blue}{-c^2b}\\
=(b-c)a^2\color{red}{-(b^2-c^2)a}\color{blue}{+bc(b-c)}\\
=(b-c)\{a^2-(b+c)a+bc\}\\
=\underline{　(b-c)(a-b)(a-c)　}\)

※\(\,3\,\)行目から\(\,4\,\)行目は共通因数として\(\,(b-c)\,\)を抜き出しています。
最終的な形は交代式の性質から
　\(\hspace{10pt}\underline{　-(a-b)(b-c)(c-a)　}\)
でも良いですね。

これは(4)の準備です。
次数の低い文字（3つとも同じなので）\(\,a\,\)で整理しただけなので、
この因数分解はすでに容易に感じるでしょう。

(4)
　\(\hspace{10pt}a^3(b-c)+b^3(c-a)+c^3(a-b)\\
=(b-c)a^3+b^3c-b^3a+c^a-c^3b\\
=\color{blue}{(b-c)a^3-(b^3-c^3)a+bc(b^2-c^2)}\)

次数が同じ交代式なので\(\,a\,\)について整理しました。

ここで、
\(\,a\,\)の\(\,1\,\)次の項の係数が
　\(\hspace{10pt}(b^3-c^3)\\
=\color{red}{(b-c)}(b^2+bc+c^2)\)
定数項が
　\(\hspace{10pt}bc(b^2-c^2)\\
=bc(b+c)\color{red}{(b-c)}\)
なので
\(\hspace{10pt}a^3(b-c)+b^3(c-a)+c^3(a-b)\\
=\color{blue}{(b-c)a^3-(b^3-c^3)a+bc(b^2-c^2)}\\
=\color{red}{(b-c)}\{a^3-(b^2+bc+c^2)a+bc(b+c)\}\)

第\(\,2\,\)因数は\(\,b\,,\,c\,\)については\(\,2\,\)次式なので\(\,bに\,\)ついて整理します。

　\(\hspace{10pt}a^3-(b^2+bc+c^2)a+bc(b+c)\\
=a^3\color{red}{-ab^2}\color{blue}{-abc}-ac^2\color{red}{+b^2c}\color{blue}{+bc^2}\\
=(c-a)b^2+(c^2-ac)b+a^3-ac^2\\
=(c-a)b^2+c(c-a)b-a(c^2-a^2)\\
=(c-a)b^2+c(c-a)b-a(c-a)(c+a)\\
=(c-a)\{b^2+cb-a(c+a)\}\\
=(c-a)(b-a)\{(b+(c+a))\}\\
=(c-a)(b-a)(a+b+c)\)

よって、\(\,(b-c)\,\)をかけて与式は
　\(\hspace{10pt}a^3(b-c)+b^3(c-a)+c^3(a-b)\\
=(b-c)\{a^3-(b^2+bc+c^2)a+bc(b+c)\}\\
=\underline{　(b-c)(c-a)(b-a)(a+b+c)　}\)

このままでも良いですが交代式であることを示しておきます。

　\(\hspace{10pt}a^3(b-c)+b^3(c-a)+c^3(a-b)\\
=\underline{　-(a-b)(b-c)(c-a)(a+b+c)　}\)

終わりです。
本当に\(\,46\,\)題でしたか？

ここまで来れば分数式になろうが文字式の計算は確実にできます。
おめでとうございます！

因数分解の問題は形が変わって尽きることはありません。
でも、ここまでできれば因数定理を組合わせれば大丈夫です。

⇒　剰余の定理（余りの定理）と因数定理の使い方と問題の解き方

自信をもっていいですよ。

⇒　3次式の展開練習問題(高校数学Ⅱ)基本から応用の24題

展開、因数分解ができれば数学ができるとはいいません。
それほどせまい世界でもありません。

しかし、どの分野でも利用する基本なので十分な練習をしておくと良いです。

⇒　式と証明の要点

数学\(\,Ⅱ\,\)からでは無くても良いですが、数学\(\,Ⅰ\,\)と分ける必要もありません。
余程自信が無いなら数学\(\,Ⅰ\,\)からやり直すと良いです。